[关闭]
@hanxiaoyang 2016-07-22T16:37:21.000000Z 字数 10425 阅读 4003

斯坦福CS231n学习笔记_(1)_基础介绍

CS231n

作者：寒小阳
时间：2015年11月。
出处：http://blog.csdn.net/han_xiaoyang/article/details/49876119
声明：版权所有，转载请注明出处，谢谢。

1.背景

计算机视觉/computer vision是一个火了N年的topic。持续化升温的原因也非常简单：在搜索/影像内容理解/医学应用/地图识别等等领域应用太多，大家都有一个愿景『让计算机能够像人一样去"看"一张图片，甚至"读懂"一张图片』。

有几个比较重要的计算机视觉任务，比如图片的分类,物体识别，物体定位于检测等等。而近年来的神经网络/深度学习使得上述任务的准确度有了非常大的提升。加之最近做了几个不大不小的计算机视觉上的项目，爱凑热闹的博主自然不打算放过此领域，也边学边做点笔记总结，写点东西，写的不正确的地方，欢迎大家提出和指正。

2.基础知识

为了简单易读易懂，这个课程笔记系列中绝大多数的代码都使用python完成。这里稍微介绍一下python和Numpy/Scipy(python中的科学计算包)的一些基础。

2.1 python基础

python是一种长得像伪代码，具备高可读性的编程语言。
优点挺多：可读性相当好，写起来也简单，所想立马可以转为实现代码，且社区即为活跃，可用的package相当多；缺点：效率一般。

2.1.1 基本数据类型

最常用的有数值型(Numbers),布尔型(Booleans)和字符串(String)三种。

可进行简单的运算，如下：

  1. x = 5
  2. print type(x) # Prints "<type 'int'>"
  3. print x       # Prints "5"
  4. print x + 1   # 加; prints "6"
  5. print x - 1   # 减; prints "4"
  6. print x * 2   # 乘; prints "10"
  7. print x ** 2  # 幂; prints "25"
  8. x += 1  #自加
  9. print x  # Prints "6"
  10. x *= 2  #自乘
  11. print x  # Prints "12"
  12. y = 2.5
  13. print type(y) # Prints "<type 'float'>"
  14. print y, y + 1, y * 2, y ** 2 # Prints "2.5 3.5 5.0 6.25"

PS：python中没有x++ 和 x-- 操作

包含True False和常见的与或非操作

  1. t = True
  2. f = False
  3. print type(t) # Prints "<type 'bool'>"
  4. print t and f # 逻辑与; prints "False"
  5. print t or f  # 逻辑或; prints "True"
  6. print not t   # 逻辑非; prints "False"
  7. print t != f  # XOR; prints "True"

字符串可以用单引号/双引号/三引号声明

  1. hello = 'hello'   
  2. world = "world"   
  3. print hello       # Prints "hello"
  4. print len(hello)  # 字符串长度; prints "5"
  5. hw = hello + ' ' + world  # 字符串连接
  6. print hw  # prints "hello world"
  7. hw2015 = '%s %s %d' % (hello, world, 2015)  # 格式化字符串
  8. print hw2015  # prints "hello world 2015"

字符串对象有很有有用的函数：

  1. s = "hello"
  2. print s.capitalize()  # 首字母大写; prints "Hello"
  3. print s.upper()       # 全大写; prints "HELLO"
  4. print s.rjust(7)      # 以7为长度右对齐，左边补空格; prints "  hello"
  5. print s.center(7)     # 居中补空格; prints " hello "
  6. print s.replace('l', '(ell)')  # 字串替换;prints "he(ell)(ell)o"
  7. print '  world '.strip()  # 去首位空格; prints "world"

2.1.2 基本容器

和数组类似的一个东东，不过可以包含不同类型的元素，同时大小也是可以调整的。

  1. xs = [3, 1, 2]   # 创建
  2. print xs, xs[2]  # Prints "[3, 1, 2] 2"
  3. print xs[-1]     # 第-1个元素，即最后一个
  4. xs[2] = 'foo'    # 下标从0开始，这是第3个元素
  5. print xs         # 可以有不同类型，Prints "[3, 1, 'foo']"
  6. xs.append('bar') # 尾部添加一个元素
  7. print xs         # Prints 
  8. x = xs.pop()     # 去掉尾部的元素
  9. print x, xs      # Prints "bar [3, 1, 'foo']"

列表最常用的操作有：
切片/slicing
即取子序列/一部分元素，如下：

  1. nums = range(5)    # 从1到5的序列
  2. print nums         # Prints "[0, 1, 2, 3, 4]"
  3. print nums[2:4]    # 下标从2到4-1的元素 prints "[2, 3]"
  4. print nums[2:]     # 下标从2到结尾的元素
  5. print nums[:2]     # 从开头到下标为2-1的元素  [0, 1]
  6. print nums[:]      # 恩，就是全取出来了
  7. print nums[:-1]    # 从开始到第-1个元素(最后的元素)
  8. nums[2:4] = [8, 9] # 对子序列赋值
  9. print nums         # Prints "[0, 1, 8, 8, 4]"

循环/loops
即遍历整个list，做一些操作，如下：

  1. animals = ['cat', 'dog', 'monkey']
  2. for animal in animals:
  3.     print animal
  4. # 依次输出 "cat", "dog", "monkey"，每个一行.

可以用enumerate取出元素的同时带出下标

  1. animals = ['cat', 'dog', 'monkey']
  2. for idx, animal in enumerate(animals):
  3.     print '#%d: %s' % (idx + 1, animal)
  4. # 输出 "#1: cat", "#2: dog", "#3: monkey"，一个一行。

List comprehension
这个相当相当相当有用，在很长的list生成过程中，效率完胜for循环：

  1. # for 循环
  2. nums = [0, 1, 2, 3, 4]
  3. squares = []
  4. for x in nums:
  5.     squares.append(x ** 2)
  6. print squares   # Prints [0, 1, 4, 9, 16]
  8. # list comprehension
  9. nums = [0, 1, 2, 3, 4]
  10. squares = [x ** 2 for x in nums]
  11. print squares   # Prints [0, 1, 4, 9, 16]

你猜怎么着，list comprehension也是可以加多重条件的：

  1. nums = [0, 1, 2, 3, 4]
  2. even_squares = [x ** 2 for x in nums if x % 2 == 0]
  3. print even_squares  # Prints "[0, 4, 16]"
  1. d = {'cat': 'cute', 'dog': 'furry'}  # 创建
  2. print d['cat']       # 根据key取出value
  3. print 'cat' in d     # 判断是否有'cat'这个key
  4. d['fish'] = 'wet'    # 添加元素
  5. print d['fish']      # Prints "wet"
  6. # print d['monkey']  # KeyError: 'monkey'非本字典的key
  7. print d.get('monkey', 'N/A')  # 有key返回value，无key返回"N/A"
  8. print d.get('fish', 'N/A')    # prints "wet"
  9. del d['fish']        # 删除某个key以及对应的value
  10. print d.get('fish', 'N/A') # prints "N/A"

对应list的那些操作，你在dict里面也能找得到：

循环/loops

  1. # for循环
  2. d = {'person': 2, 'cat': 4, 'spider': 8}
  3. for animal in d:
  4.     legs = d[animal]
  5.     print 'A %s has %d legs' % (animal, legs)
  6. # Prints "A person has 2 legs", "A spider has 8 legs", "A cat has 4 legs"
  8. # 通过iteritems
  9. d = {'person': 2, 'cat': 4, 'spider': 8}
  10. for animal, legs in d.iteritems():
  11.     print 'A %s has %d legs' % (animal, legs)
  12. # Prints "A person has 2 legs", "A spider has 8 legs", "A cat has 4 legs"
  1. # Dictionary comprehension
  2. nums = [0, 1, 2, 3, 4]
  3. even_num_to_square = {x: x ** 2 for x in nums if x % 2 == 0}
  4. print even_num_to_square  # Prints "{0: 0, 2: 4, 4: 16}"
  1. d = {(x, x + 1): x for x in range(10)}  # 创建
  2. t = (5, 6)       # Create a tuple
  3. print type(t)    # Prints "<type 'tuple'>"
  4. print d[t]       # Prints "5"
  5. print d[(1, 2)]  # Prints "1"

2.1.3 函数

用def可以定义一个函数：

  1. def sign(x):
  2.     if x > 0:
  3.         return 'positive'
  4.     elif x < 0:
  5.         return 'negative'
  6.     else:
  7.         return 'zero'
  9. for x in [-1, 0, 1]:
  10.     print sign(x)
  11. # Prints "negative", "zero", "positive"
  1. def hello(name, loud=False):
  2.     if loud:
  3.         print 'HELLO, %s' % name.upper()
  4.     else:
  5.         print 'Hello, %s!' % name
  7. hello('Bob') # Prints "Hello, Bob"
  8. hello('Fred', loud=True)  # Prints "HELLO, FRED!"

python里面的类定义非常的直接和简洁：

  1. class Greeter:
  3.     # Constructor
  4.     def __init__(self, name):
  5.         self.name = name  # Create an instance variable
  7.     # Instance method
  8.     def greet(self, loud=False):
  9.         if loud:
  10.             print 'HELLO, %s!' % self.name.upper()
  11.         else:
  12.             print 'Hello, %s' % self.name
  14. g = Greeter('Fred')  # Construct an instance of the Greeter class
  15. g.greet()            # Call an instance method; prints "Hello, Fred"
  16. g.greet(loud=True)   # Call an instance method; prints "HELLO, FRED!"

2.2.NumPy基础

NumPy是Python的科学计算的一个核心库。它提供了一个高性能的多维数组(矩阵)对象，可以完成在其之上的很多操作。很多机器学习中的计算问题，把数据vectorize之后可以进行非常高效的运算。

2.2.1 数组

一个NumPy数组是一些类型相同的元素组成的类矩阵数据。用list或者层叠的list可以初始化：

  1. import numpy as np
  3. a = np.array([1, 2, 3])  # 一维Numpy数组
  4. print type(a)            # Prints "<type 'numpy.ndarray'>"
  5. print a.shape            # Prints "(3,)"
  6. print a[0], a[1], a[2]   # Prints "1 2 3"
  7. a[0] = 5                 # 重赋值
  8. print a                  # Prints "[5, 2, 3]"
  10. b = np.array([[1,2,3],[4,5,6]])   # 二维Numpy数组
  11. print b.shape                     # Prints "(2, 3)"
  12. print b[0, 0], b[0, 1], b[1, 0]   # Prints "1 2 4"

生成一些特殊的Numpy数组(矩阵)时，我们有特定的函数可以调用：

  1. import numpy as np
  3. a = np.zeros((2,2))  # 全0的2*2 Numpy数组
  4. print a              # Prints "[[ 0.  0.]
  5.                      #          [ 0.  0.]]"
  7. b = np.ones((1,2))   # 全1 Numpy数组
  8. print b              # Prints "[[ 1.  1.]]"
  10. c = np.full((2,2), 7) # 固定值Numpy数组
  11. print c               # Prints "[[ 7.  7.]
  12.                       #          [ 7.  7.]]"
  14. d = np.eye(2)        # 2*2 对角Numpy数组
  15. print d              # Prints "[[ 1.  0.]
  16.                      #          [ 0.  1.]]"
  18. e = np.random.random((2,2)) # 2*2 的随机Numpy数组
  19. print e                     # 随机输出

2.2.2 Numpy数组索引与取值

可以通过像list一样的分片/slicing操作取出需要的数值部分。

  1. import numpy as np
  3. # 创建如下的3*4 Numpy数组
  4. # [[ 1  2  3  4]
  5. #  [ 5  6  7  8]
  6. #  [ 9 10 11 12]]
  7. a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
  9. # 通过slicing取出前两行的2到3列:
  10. # [[2 3]
  11. #  [6 7]]
  12. b = a[:2, 1:3]
  14. # 需要注意的是取出的b中的数据实际上和a的这部分数据是同一份数据.
  15. print a[0, 1]   # Prints "2"
  16. b[0, 0] = 77    # b[0, 0] 和 a[0, 1] 是同一份数据
  17. print a[0, 1]   # a也被修改了，Prints "77"
  1. import numpy as np
  3. a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
  5. row_r1 = a[1, :]    # a 的第二行  
  6. row_r2 = a[1:2, :]  # 同上
  7. print row_r1, row_r1.shape  # Prints "[5 6 7 8] (4,)"
  8. print row_r2, row_r2.shape  # Prints "[[5 6 7 8]] (1, 4)"
  10. col_r1 = a[:, 1]
  11. col_r2 = a[:, 1:2]
  12. print col_r1, col_r1.shape  # Prints "[ 2  6 10] (3,)"
  13. print col_r2, col_r2.shape  # Prints "[[ 2]
  14.                             #          [ 6]
  15.                             #          [10]] (3, 1)"

还可以这么着取：

  1. import numpy as np
  3. a = np.array([[1,2], [3, 4], [5, 6]])
  5. # 取出(0,0) (1,1) (2,0)三个位置的值
  6. print a[[0, 1, 2], [0, 1, 0]]  # Prints "[1 4 5]"
  8. # 和上面一样
  9. print np.array([a[0, 0], a[1, 1], a[2, 0]])  # Prints "[1 4 5]"
  11. # 取出(0,1) (0,1) 两个位置的值
  12. print a[[0, 0], [1, 1]]  # Prints "[2 2]"
  14. # 同上
  15. print np.array([a[0, 1], a[0, 1]])  # Prints "[2 2]"

我们还可以通过条件得到bool型的Numpy数组结果，再通过这个数组取出符合条件的值，如下：

  1. import numpy as np
  3. a = np.array([[1,2], [3, 4], [5, 6]])
  5. bool_idx = (a > 2)  # 判定a大于2的结果矩阵
  7. print bool_idx      # Prints "[[False False]
  8.                     #          [ True  True]
  9.                     #          [ True  True]]"
  11. # 再通过bool_idx取出我们要的值
  12. print a[bool_idx]  # Prints "[3 4 5 6]"
  14. # 放在一起我们可以这么写
  15. print a[a > 2]     # Prints "[3 4 5 6]"

Numpy数组的类型

  1. import numpy as np
  3. x = np.array([1, 2])  
  4. print x.dtype         # Prints "int64"
  6. x = np.array([1.0, 2.0]) 
  7. print x.dtype             # Prints "float64"
  9. x = np.array([1, 2], dtype=np.int64)  # 强制使用某个type
  10. print x.dtype                         # Prints "int64"

2.2.3 Numpy数组的运算

矩阵的加减开方和(元素对元素)乘除如下：

  1. import numpy as np
  3. x = np.array([[1,2],[3,4]], dtype=np.float64)
  4. y = np.array([[5,6],[7,8]], dtype=np.float64)
  6. # [[ 6.0  8.0]
  7. #  [10.0 12.0]]
  8. print x + y
  9. print np.add(x, y)
  11. # [[-4.0 -4.0]
  12. #  [-4.0 -4.0]]
  13. print x - y
  14. print np.subtract(x, y)
  16. # 元素对元素，点对点的乘积
  17. # [[ 5.0 12.0]
  18. #  [21.0 32.0]]
  19. print x * y
  20. print np.multiply(x, y)
  22. # 元素对元素，点对点的除法
  23. # [[ 0.2         0.33333333]
  24. #  [ 0.42857143  0.5       ]]
  25. print x / y
  26. print np.divide(x, y)
  28. # 开方
  29. # [[ 1.          1.41421356]
  30. #  [ 1.73205081  2.        ]]
  31. print np.sqrt(x)

矩阵的内积是通过下列方法计算的：

  1. import numpy as np
  3. x = np.array([[1,2],[3,4]])
  4. y = np.array([[5,6],[7,8]])
  6. v = np.array([9,10])
  7. w = np.array([11, 12])
  9. # 向量内积，得到 219
  10. print v.dot(w)
  11. print np.dot(v, w)
  13. # 矩阵乘法，得到 [29 67]
  14. print x.dot(v)
  15. print np.dot(x, v)
  17. # 矩阵乘法
  18. # [[19 22]
  19. #  [43 50]]
  20. print x.dot(y)
  21. print np.dot(x, y)

特别特别有用的一个操作是，sum/求和(对某个维度)：

  1. import numpy as np
  3. x = np.array([[1,2],[3,4]])
  5. print np.sum(x)  # 整个矩阵的和，得到 "10"
  6. print np.sum(x, axis=0)  # 每一列的和 得到 "[4 6]"
  7. print np.sum(x, axis=1)  # 每一行的和 得到 "[3 7]"

还有一个经常会用到操作是矩阵的转置，在Numpy数组里用.T实现：

  1. import numpy as np
  3. x = np.array([[1,2], [3,4]])
  4. print x    # Prints "[[1 2]
  5.            #          [3 4]]"
  6. print x.T  # Prints "[[1 3]
  7.            #          [2 4]]"
  9. # 1*n的Numpy数组，用.T之后其实啥也没做:
  10. v = np.array([1,2,3])
  11. print v    # Prints "[1 2 3]"
  12. print v.T  # Prints "[1 2 3]"

2.2.4 Broadcasting

Numpy还有一个非常牛逼的机制，你想想，如果你现在有一大一小俩矩阵，你想使用小矩阵在大矩阵上做多次操作。额，举个例子好了，假如你想将一个1*n的矩阵，加到m*n的矩阵的每一行上：

  1. #你如果要用for循环实现是酱紫的(下面用y的原因是，你不想改变原来的x)
  2. import numpy as np
  4. x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
  5. v = np.array([1, 0, 1])
  6. y = np.empty_like(x)   # 设置一个和x一样维度的Numpy数组y
  8. # 逐行相加
  9. for i in range(4):
  10.     y[i, :] = x[i, :] + v
  12. # 恩，y就是你想要的了
  13. # [[ 2  2  4]
  14. #  [ 5  5  7]
  15. #  [ 8  8 10]
  16. #  [11 11 13]]
  17. print y
  1. #上一种方法如果for的次数非常多，会很慢，于是我们改进了一下
  2. import numpy as np
  4. x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
  5. v = np.array([1, 0, 1])
  6. vv = np.tile(v, (4, 1))  # 变形，重复然后叠起来
  7. print vv                 # Prints "[[1 0 1]
  8.                          #          [1 0 1]
  9.                          #          [1 0 1]
  10.                          #          [1 0 1]]"
  11. y = x + vv  # 相加
  12. print y  # Prints "[[ 2  2  4
  13.          #          [ 5  5  7]
  14.          #          [ 8  8 10]
  15.          #          [11 11 13]]"
  1. #其实因为Numpy的Broadcasting，你可以直接酱紫操作
  2. import numpy as np
  4. x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
  5. v = np.array([1, 0, 1])
  6. y = x + v  # 直接加！！！
  7. print y  # Prints "[[ 2  2  4]
  8.          #          [ 5  5  7]
  9.          #          [ 8  8 10]
  10.          #          [11 11 13]]"

更多Broadcasting的例子请看下面：

  1. import numpy as np
  3. v = np.array([1,2,3])  # v has shape (3,)
  4. w = np.array([4,5])    # w has shape (2,)
  5. # 首先把v变成一个列向量
  6. # v现在的形状是(3, 1);
  7. # 作用在w上得到的结果形状是(3, 2)，如下
  8. # [[ 4  5]
  9. #  [ 8 10]
  10. #  [12 15]]
  11. print np.reshape(v, (3, 1)) * w
  13. # 逐行相加
  14. x = np.array([[1,2,3], [4,5,6]])
  15. # 得到如下结果:
  16. # [[2 4 6]
  17. #  [5 7 9]]
  18. print x + v
  20. # 先逐行相加再转置，得到以下结果:
  21. # [[ 5  6  7]
  22. #  [ 9 10 11]]
  23. print (x.T + w).T
  24. # 恩，也可以这么做
  25. print x + np.reshape(w, (2, 1))

2.3 SciPy

Numpy提供了一个非常方便操作和计算的高维向量对象，并提供基本的操作方法，而Scipy是在Numpy的基础上，提供很多很多的函数和方法去直接完成你需要的矩阵操作。有兴趣可以浏览Scipy方法索引查看具体的方法，函数略多，要都记下来有点困难，随用随查吧。

向量距离计算

需要特别拎出来说一下的是，向量之间的距离计算，这个Scipy提供了很好的接口scipy.spatial.distance.pdist：

  1. import numpy as np
  2. from scipy.spatial.distance import pdist, squareform
  4. # [[0 1]
  5. #  [1 0]
  6. #  [2 0]]
  7. x = np.array([[0, 1], [1, 0], [2, 0]])
  8. print x
  10. # 计算矩阵每一行和每一行之间的欧氏距离
  11. # d[i, j] 是 x[i, :] 和 x[j, :] 之间的距离,
  12. # 结果如下：
  13. # [[ 0.          1.41421356  2.23606798]
  14. #  [ 1.41421356  0.          1.        ]
  15. #  [ 2.23606798  1.          0.        ]]
  16. d = squareform(pdist(x, 'euclidean'))
  17. print d

2.4 Matplotlib

这是python中的一个作图工具包。如果你熟悉matlab的语法的话，应该会用得挺顺手。可以通过matplotlib.pyplot.plot了解更多绘图相关的设置和参数。

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. # 计算x和对应的sin值作为y
  5. x = np.arange(0, 3 * np.pi, 0.1)
  6. y = np.sin(x)
  8. # 用matplotlib绘出点的变化曲线
  9. plt.plot(x, y)
  10. plt.show()  # 只有调用plt.show()之后才能显示

结果如下：
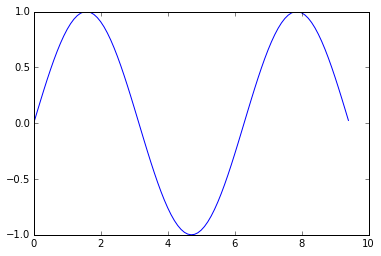
sin图像

  1. # 在一个图中画出2条曲线
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  5. # 计算x对应的sin和cos值
  6. x = np.arange(0, 3 * np.pi, 0.1)
  7. y_sin = np.sin(x)
  8. y_cos = np.cos(x)
  10. # 用matplotlib作图
  11. plt.plot(x, y_sin)
  12. plt.plot(x, y_cos)
  13. plt.xlabel('x axis label')
  14. plt.ylabel('y axis label')
  15. plt.title('Sine and Cosine')
  16. plt.legend(['Sine', 'Cosine'])
  17. plt.show()

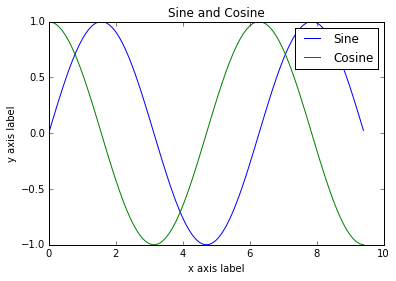
sin和cos

  1. # 用subplot分到子图里
  2. import numpy as np
  3. import matplotlib.pyplot as plt
  5. # 得到x对应的sin和cos值
  6. x = np.arange(0, 3 * np.pi, 0.1)
  7. y_sin = np.sin(x)
  8. y_cos = np.cos(x)
  10. # 2*1个子图，第一个位置.
  11. plt.subplot(2, 1, 1)
  13. # 画第一个子图
  14. plt.plot(x, y_sin)
  15. plt.title('Sine')
  17. # 画第2个子图
  18. plt.subplot(2, 1, 2)
  19. plt.plot(x, y_cos)
  20. plt.title('Cosine')
  22. plt.show()

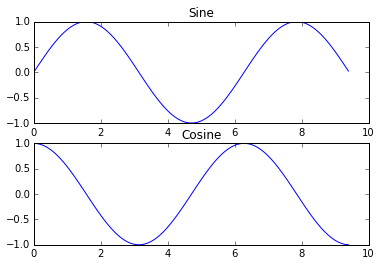
subplot

2.5 简单图片读写

可以使用imshow来显示图片。

  1. import numpy as np
  2. from scipy.misc import imread, imresize
  3. import matplotlib.pyplot as plt
  5. img = imread('/Users/HanXiaoyang/Comuter_vision/computer_vision.jpg')
  6. img_tinted = img * [1, 0.95, 0.9]
  8. # 显示原始图片
  9. plt.subplot(1, 2, 1)
  10. plt.imshow(img)
  12. # 显示调色后的图片
  13. plt.subplot(1, 2, 2)
  14. plt.imshow(np.uint8(img_tinted))
  16. plt.show()

computer_vision

参考资料与原文

cs231n python/Numpy指南

添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注