@hanbingtao 2025-06-05T09:08:46.000000Z 字数 4754 阅读 139

零基础入门深度学习(8) - Transformer (1/3)

大模型 深度学习入门

时隔八年，再次提笔续写这个系列。毫无疑问，智能时代已经到来，AGI（通用人工智能）似乎也不再是遥不可及的梦想。大模型，作为目前最接近实现AGI的技术，甚至已经可以写代码了！这对于程序员真是数十年未有之大变局，因此学好、用好大模型，就将一步跨过JavaScript、Java、C++直接走到鄙视链的顶端，用自然语言编程，成为超级程序员。希望这个系列帮助你快速从零基础达到真入门级水平，理解大模型才能用好大模型。零基础意味着你不需要太多的数学知识，只要会写程序就行了。虽然文中会有很多公式你也许看不懂，但同时也会有更多的代码，程序员的你一定能看懂的（我周围是一群狂热的Clean Code程序员，所以我写的代码也不会很差）。

文章列表

往期回顾

在前面的文章中，我们介绍了全连接神经网络、卷积神经网络、循环神经网络等，可以它们看做是不同结构的神经网络。本文将继续从结构这个角度出发，介绍一种新的、极其重要的神经网络结构：Transformer。从时间来看，它也不是那么新，毕竟是2017年出现的，到现在（2025年）也将近十年了。然而，没有一个更新的网络结构比它还成功，也说明其结构设计是极为优秀的。Transformer出现后，用了5年左右的时间，逐渐取代卷积神经网络成为当红一哥，又用另外5年开辟了一个全新的时代：大模型时代。可以说，目前所有的大模型，都是以Transformer结构为基础的各种变体。如果您刚刚开始学习AI，可以尝试快速跳过Transformer之前的部分，把主要的精力放在Transformer的学习上。

由于Transformer内容较多，为了保持一个良好的节奏，我将整个内容分成三个部分。第一部分比较简单，是一些基础知识的介绍；第二部分重点讲述transformer的注意力机制，这也是它的核心部分；第三部分讲述模型的整体结构，以及训练和推理。

Transformer为什么牛

Transformer是作为RNN的竞争对手被发明出来的，它们所要解决的问题是一样的，即对序列数据进行建模。关于序列数据建模，大家可以回看零基础入门深度学习(5) - 循环神经网络，语言模型就是一个很好的例子。也如同我们在之前文章中说的，在序列长度较长的时候，RNN会面临严重梯度消失和梯度爆炸，导致其对长序列建模效果很差。LSTM（回看零基础入门深度学习(6) - 长短时记忆网络(LSTM)）使这个问题得到了一些改善，并在相当长的一段时间里成为序列建模的主要模型，广泛用于机器翻译、文档摘要、代码生成等各种任务中。Transformer最初是用来做机器翻译的，一经发明便一鸣惊人，迅速取代了LSTM成为序列建模的首选模型，在随后几年更是被成功用在其它领域（如声音、图像、视频处理等），最终开辟了一个叫做多模态模型的全新赛道。这说明Transformer结构具备极佳的通用性。

Transformer架构的另一个优点是极佳的可扩展性，即模型的能力随着模型参数量增加而增强的能力。可扩展性在深度神经网络中是普遍存在的，但Transformer格外优秀。例如，卷积神经网络的参数量通常是在几百万到几亿之间，再大也不是不行，但在性能上看不到收益。也就是说，数十亿参数的卷积神经网络并不比数亿参数强多少，模型参数规模扩展收益很低，达到了规模瓶颈。和卷积神经网络相比，Transformer的可扩展性要强得多，当模型参数量扩展到数千亿时，仍然能够得到明显性能增益。正是由于这个优点，模型变得越来越大，从而又开辟了一个叫做大模型新赛道。

Transformer结构携通用型和可扩展性两大优势，再加上后来预训练技术加持，产生了基础模型，即可以同时满足成百上千个任务需求的、强大的单一模型。从此，开发AI应用时再也不用为每一个应用场景单独训练一个模型，而是直接使用基础模型或在其基础上精调训练专用模型，从而极大降低了每个场景AI开发难度和成本，使AI真正赋能千行百业并走进我们的生活、娱乐、学习和工作。因此，毫不夸张的说，Transformer改变了整个深度学习的历史。

序列的表示

既然Transfomer是给序列建模的模型，我们讲解Transformer之前，首先要把如何表示序列讲清楚。序列可以是一段文本，例如：

我昨天上学迟到了，老师批评了____。

为了表示这段文本，我们首先需要一个词表，它是可能出现的词的全集。词表中放入哪些词（Token），可以完全由设计者决定。例如，如果想表达所有的中文，那么把所有的中文字放进词表就可以；如果还想表达多语种，那么就需要把各个语言中的词放进去；如果还想表达数学公式、制表符、表情符号、颜文字...那么词表里面就需要放入更多的词。当前大模型的词表，通常的大小为数万到十几万。有了词表之后，我们可以通过一个词在词表中的位置来表示这个词。

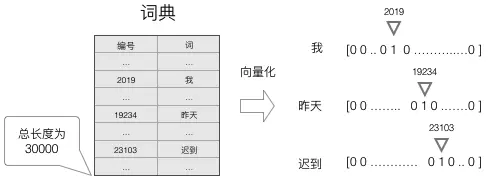
如上图所示，假设我们有一个长度为30000的词表，其中，“我”在词表2019这个位置，“昨天”在词表19234这个位置，“迟到”在23103这个位置，那么，“我昨天迟到”就可以用一个包含三个数字的序列来表示：

2019, 19234, 23103

大家可能发现一个问题，就是序列的可组合性，即序列和序列可以组成新的序列。由于可组合性的存在，词表的方案就不是唯一的。例如，此表中可能没有“昨天”这个词，但是有“昨”和“天”两个字，那么，就可以用“昨”和“天”那个字所对应的数字，来组合表示“昨天”，当然同“昨天”相比，编码“我昨天迟到”就需要4个Token而不是3个。显然，不同的方案编码效率是不同的，好的编码方案可以用更少Token数量表达更多的语义。目前获得一个“好”词表的方法，基本上是还海量语料中统计不同每个词的词频，优先把更高词频的词放到词表中。这里面的“词”也比我们自然语言中的“词”含义更为广泛，它可以是一个字、一个词、一个短语、甚至只是一个词缀或单个字母。例如，英语中ing这个后缀经常出现，很多时候都会把ing放到词表中。从语料生成词表的算法很多，例如BPE（Byte Pair Encoder，字节对编码），大家感兴趣可以从专门的资料中学习，本文不再赘述。

只用一个数字表示词，并没有太多的语义信息，例如，模型很难仅仅从2019这个数字中挖掘出“我”这个词所代表的语义。为此，词嵌入这个方法被发明出来。所谓嵌入，就是构造一个高维语义空间，然后将每个词嵌入到语义空间中（即每个词都是语义空间中的一个点）。常用的训练词嵌入算法有Word2Vec、Glove、BERT（后续文章会讲）等，感兴趣可以从专门资料中学习，本文不再赘述。

通过词嵌入，为词表中的每个词分配一个向量（即词向量），词向量的维度就是语义空间的维度，可能是512（Transformer），甚至是12288（GPT3），语义空间的维度越高，语义表达能力越强。语义空间通常被定义为连续空间，因此词向量的每个值都是浮点数。例如，语义空间维度是512时，每个词向量就包含了512个浮点数，而不是之前的单一一个数字。同时，词向量之间的距离也和词的语义距离相关，语义相似的词，词向量之间的距离小；反之词向量的距离就大。通过使用带语义的词向量，而非单一数字来表征每个Token，模型就可以获取到丰富的语义的信息。下图是语义空间的一个例子：

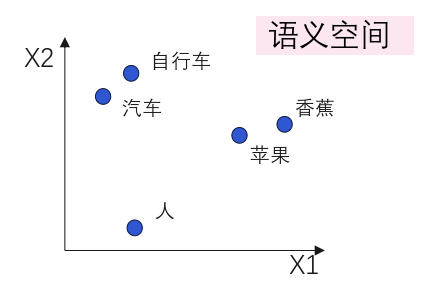
假设语义空间维度为 $D$ ，词表大小为 $V$ ，则全部词向量可以保存在一个 $M\in\mathbb{R}^{V\times D}$ 的矩阵里，矩阵每一行保存一个词向量，一个词在词表中是第几个，那么它对应的词向量就保存在矩阵的第几行。通过查表操作，就可以很方便的将表示一个词的数字转换为词向量。假设有如下的词嵌入矩阵：

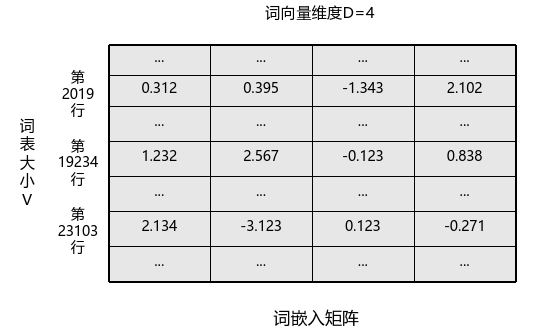
那么，“我昨天迟到”会被表示为：

[0.312, 0.395, -1.343, 2.102], [1.232, 2.567, -0.123, 0.838], [2.134, -3.123, 0.123, -0.271]

这三个词向量可以被放到一个矩阵中：

$X=\begin{bmatrix} 0.312 & 0.395 & -1.343 & 2.102\\ 1.232 & 2.567 & -0.123 & 0.838\\ 2.134 & -3.123 & 0.123 & -0.271\\ \end{bmatrix}$

大功告成！读者至此可以了解，每一个文字序列，最终都可以被表达为一个词向量组成的矩阵，我们每次向Transformer输入一个文字序列时，实际上输入的就是这个矩阵。

位置编码

把序列表示为词向量矩阵就可以为模型提供足够的信息了么？答案是否定的。我们需要思考一个问题：如何告诉模型序列内各个元素的顺序？我们知道，语言中每个词的顺序是极其重要的，顺序变了，那意思肯定就全乱套了。最容易想到的办法，就是我要给序列中的每个字一个编号，这样模型不就知道顺序了么？这个想法类似这样，当我想向模型输入“我昨天迟到”时，我会输入：

1我 2昨天 3迟到

我可真是个大聪明，通过给每个字打上它的位置编号，就能够将序列的顺序输入给模型了。当然，模型理不理解、如何理解是另一回事，至少该传递的信息我都传递了。

那么，接下来就是要考虑如何编码这个位置编号了。前面我们讲过，词是通过词嵌入的方式，将其编码为词向量来表达的。那么，位置该如何编码呢？实际上位置编码方案非常多，后面的文章会介绍。本文只介绍一种非常简单的位置编码方式（也是Transformer最初使用的）。

采用不同频率的正弦和余弦函数：

$PE_{(pos,2i)} = \sin(\frac{pos}{10000^{2i/d}})\\ PE_{(pos,2i+1)} = \cos(\frac{pos}{10000^{2i/d}})$
其中

$pos$ 表示位置，

$i$ 表示词向量维度，即每个位置编码维度对应一个正弦波，波长从

$2π$ 到

$10000·2π$ 呈几何级数递增。Transformer选择这一函数是因为假设它能方便模型学习基于相对位置的注意力机制，因为对于任何固定偏移量

$k$ ，

$PE_{pos+k}$ 可以表示为

$PE_{pos}$ 的线性函数。

假设词向量维度 $D=4$ ，则前三个Token的位置编码向量为（代入上述公式计算即可）：

[0, 0, 1, 1], [0.84, 0.0001, 0.54, 1], [0.91, 0.0002, 0.42, 1]

和词向量一样，我们也可以把它们放到一个矩阵中：

$P=\begin{bmatrix} 0 & 0 & 1 & 1\\ 0.84 & 0.0001 & 0.54 & 1\\ 0.91 & 0.0002 & 0.42 & 1\\ \end{bmatrix}$

那么，如何把位置编码和词向量合并到一起输入给模型呢？Transfomer采用的方式就是直接将两个矩阵相加：

$X' = X + P$

并将得到的 $X'$ 作为模型的输入，这样，模型就同时得到了文本序列的词和词序信息。

小节

本文介绍了一些非常基础的知识，包括如何表征序列，什么是Token，以及如何通过位置编码表达序列中Token的顺序。这些知识是学习Transformer的基础，希望读者能够理解。下篇文章，我们将介绍Transformer的核心：注意力机制。

参考资料

Attenion Is All You Need