@blueGhost 2017-07-28T03:08:42.000000Z 字数 5456 阅读 1776

二：卷积神经网络入门

deepLearning

本文翻译自Adit Deshpande的博客：
A Beginner's Guide To Understanding Convolutional Neural Networks Part 2

01.png-1114.3kB

简介

在这一篇章，我们会展开讨论一下卷积神经网络的一些细节。不过，某些课题比较复杂，难以在此展开，则会提供链接到相应的论文，以供参考。

步长(stride)和填充(padding)

上篇我们讲到卷积（convolving），卷积层（Convolutional Layer），神经元（filter／neuron／kernel），感知区域（receptive field）等概念。影响卷积效果的，除了神经元的大（size of filter），还有2个主要参数：步长（stride）和填充（padding）。

上一篇我们举了个卷积的例子（一个5x5的filter在32x32的图片上卷积，输出一个28x28的激活图［Activation map］），该例子，filter从左到右、由上往下卷积，每次移动一个像素位，这个“每次移动的距离”就是“步长”（Stride）。Stride通常设置成一个可以使激活图边长为整数的数值。下面我们看一个例子：
假设输入一个7x7的数据矩阵，使用3x3的filter进行卷积，步长为1，则效果如下：
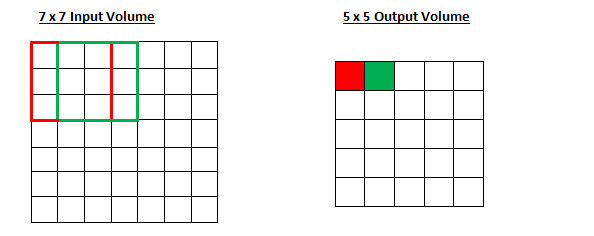
Stride1.png-5.6kB

如果现在把步长变成2呢？
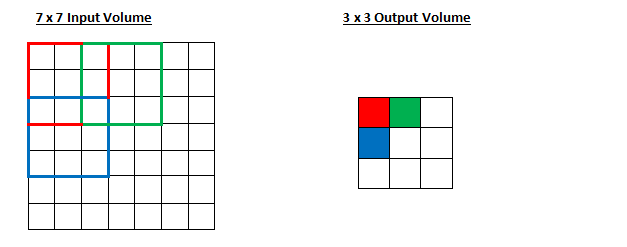
Stride2.png-5.4kB

可以看到，输出的激活图变小了，如果我们将步长增加到3呢？你会发现无法使输出的激活图边长为整数。通常，卷积神经网络的编程人员会通过加大步长来减少卷积时感知区域的重叠程度，同时最终获得更小的激活图。

接下来讲讲填充（padding）。我们先考虑一下：当步长为1，filters为5x5x3，输入为32x32x3，卷积一次后，得到28x28x3的矩阵。明显的，输出的矩阵变小了，如果持续的卷积，可以发现输出越来越小。在前几层卷积，我们希望输出不要变小得太快，以便保留更多的信息，检测更多的低层次特征。
假如我们说，上面的例子，我们想得到的输出仍然是32x32x3。我们可以给输入添加一个厚度为2、值为0的填充，此时我们得到一个36x36x3的输入。
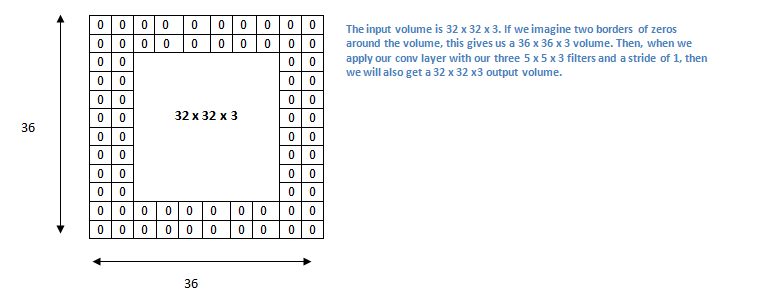
Pad.png-10.9kB

如果你的步长为1，可以通过以下公式(1)计算出填充的厚度（K是filter的大小）

${ Zero Padding=\frac{K-1}{2} (1) }$

下面这个公式可以计算出卷积后输出的大小（O是输出的大小，W是输入的大小，K是filter的大小，P是填充的厚度，S是步长）

${ O= \frac{W-K+2P}{S}+1 (2) }$

超参数的取值

如何确定CNNs需要多少层？多少个卷积层？filter的大小？步长的大小？填充的大小？到现在，这些参数的确定，没有一个标准的参考。这是因为神经网络很大程度取决于你所拥有的数据以及你想让神经网络做什么事。不同大小、类别、和复杂度的图片，其数据也不同。所以，你需要根据不同的场景和数据，找出一套参数，使得特征提取和识别达到最优。

线性整流层[ReLU（Rectified Linear Units）Layers]

在卷积层之后，立即加入一个非线性层（nonlinear lay/ 也叫激活层activation layer）对数据进行非线性化处理，非常重要。卷积层的数字操作，都是一些线性计算，仅仅是元素之间的相乘和相加，这样，就没有必要组织多层的神经网络了，因为一层直接做完所有的线性运算就达到效果了。
过去，常用tanh，sigmoid这两个非线性函数来对数据进行非线性化。然而，研究证明ReLU layers远比这两个函数的效果要好。
ReLU可以提升计算效率从而大大缩短训练时间，同时对精确度又不会造成太大的影响。另外，它还有助于避免“梯度消失问题”（the gradient vanishing problem）。线性整流层(The ReLU layer)通过 $f(x)=max(0,x)$ 处理输入的数据，就是将负数变为0，正数保持不变。线性整流层增加了模型和网络的非线性属性，同时不影响卷积层的感知区域(without affecting the receptive fields of the cov layer)。
更详细可参考深度学习之父Geoffrey Hinton的论文。

池化层（Pooling Layers）

进行了线性整流后（ReLU layers），编程人员可以选择加入池化层（Pooling layer，通常也称为“向下采样层”［Downsampling layer］）。
池化层可以有多种方式，其中“最大池化”（maxpooling）是最常用的方式。
maxpooling的做法是，使用一个filter（通常是2x2），用相同长度的步长（即stride为2）对输入的数据进行卷积，输出每个被卷积区域的最大值。如下图：
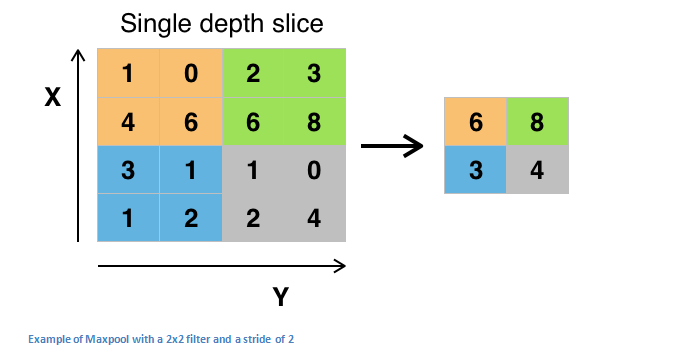
MaxPool.png-16.1kB
其它池化方式还包括“平均池化”（average pooling）和L2-norm pooling。
池化的内在逻辑是：一旦我们知道某个特征存在于原始输入中（即有比较大的激活值），“该特征所在的确切位置”相比于“该特征与其它特征的相对位置”并没有那么重要。（The intuitive reasoning behind this layer is that once we know that a specific feature is in the original input volume (there will be a high activation value), its exact location is not as important as its relative location to the other features.）
池化层极大的减少了输入的数据的维度（长和宽减少，深度没有减少），这样有两个重要作用：

1)将数据的个数减少了75％（按照前面举的例子），降低了计算成本
2)控制了过度拟合（overfitting）。过度拟合指的是神经网络在训练集中表现上佳，但是在测试集中却表现渣渣。比如在测试集中准确率为100%或者99%，而在测试集中准确率只有50%。

丢弃层（Dropout Layers）

丢弃层在神经网络中提供很特别的功能。我们上面讲到过“过度拟合问题”（overfitting），即在训练集中表现上佳，一旦拿到其它数据集合运作，却表现糟糕。
丢弃层会随机“丢弃”某些激活值（在正向[forward pass]中通过将激活值设置为0来实现）（This layer “drops out” a random set of activations in that layer by setting them to zero in the forward pass）。
为什么这么做呢？可以这么说，它强迫神经网络提高容错性（it forces the network to be redundant）。神经网络必须在丢失了一些激活数据后，还是能够准确的输出。这保证了神经网络不会太过拟合训练集的数据，帮助避免过度拟合问题。非常重要的，丢弃层只在训练过程中使用

关于丢弃层，详参Geoffrey Hinton的论文。

Network in Network Layers

Network in Network Layer使用一个1x1的filter对输入的数据进行卷积。（A network in network layer refers to a conv layer where a 1 x 1 size filter is used.）
你可能会疑惑：通常一个卷积层，filter的边长是大于1的，这样才能在输入中提取到特征，而这个1x1的filter没有这个作用。
其实，Network in Network Layer能够加深数据的深度（即不改变输入数据的长度length和宽度width，但增大了深度depth）。想象一下，我们对输入的数据施加1x1xN的卷积（用n个1x1的filter去卷积），则会得到N层数据（每一个filter卷积完输入的数据就得到一层和输入数据一样长宽的数据）。Effectively, this layer is performing a N-D element-wise multiplication where N is the depth of the input volume into the layer.

详参Min Lin的论文

分类（Classification）, 定位（Localization）, 检测（Detection）, （分割）Segmentation

这个博客系列中，part1我们介绍了“图像分类／识别”（image classification）。过程就是输入一个图片，得出图片所属的分类。
当我们的任务是物体定位时（Object localization），我们不仅要做分类(classification)，还要在图片中把物体圈起来。
Localization.png-224.6kB

物体检测（object detection），需要将图片中的所有物体定位出来。所以你可能有多个框框把各个识别出来的物体圈起来。
最后，物体分割（object segmentation）是识别出物体并把物体的边缘勾画出来。
Detection.png-319.5kB

在本系列博客的part3将会介绍这些是如何做到的。不过如果你等不及了，可以先看下面这些资料：

检测／定位（detection/localization）：
RCNN, Fast RCNN, Faster RCNN, MultiBox, Bayesian Optimization, Multi-region, RCNN Minus R, Image Windows

分割（segmentation）:
Semantic Seg, Unconstrained Video, Shape Guided, Object Regions, Shape Sharing

迁移学习（Transfer Learning）

现在，在深度学习社区，有一个普遍的错误认知：没有Google那么多数据，你不可能创建有效的深度学习模型。尽管数据对神经网络的创建非常重要，迁移学习（transfer learning）降低了神经网络对数据的依赖。

迁移学习是指，以一个已经训练过的模型（“已经训练过”指的是，该神经网络已经过大量数据的训练，参数均已得到调优）为基础，在此基础上在自己的数据集上继续“调优”。（Transfer learning is the process of taking a pre-trained model (the weights and parameters of a network that has been trained on a large dataset by somebody else) and “fine-tuning” the model with your own dataset.）。这样，已经训练过的模型（the pre-trained model）作为“特征提取器”（feature extractor）。你需要做的是将预训练过的神经网络的最后一层（the last layer）置换成你自己的分类器（classifier，这个分类器取决于你的问题域[problem space]是什么）。然后冻结其它层的参数和权重，开始在你的训练集上训练你的神经网络。（冻结参数，指的是在训练过程中，不改变这些参数）。

让我们来看看这是如何实现的。假如我们有一个在ImageNet（一个有1400万图片包含1000个类别的图片数据库）训练好的模型。我们知道在这个神经网络的低级层次（lower layers of the network），功能是检测基础特征，比如边角和曲线。那么，除非你自己的模型要解决的问题非常特殊，数据集也非常特别，否则你的模型也是要检测这些基础特征的。这样，你就可以不用从随机的参数和权重开始训练你的神经网络，你可以复用预训练过的模型的参数（冻结这些参数），把训练重点放在你的问题领域内重要的层上。如果你的数据集（dataset）和ImageNet图片的差异比较大，那么需要训练的层会比较多，因为你只能复用一些低级层次。

迁移学习详参：
Yoshua Bengio（一位深度学习领域的先驱）的论文
 Ali Sharif Razavian的论文
 Jeff Donahue的论文

数据增强技术（Data Augmentation Techniques）

我们知道数据对于CNNs来说非常重要，数据增强（data augmentation）可以使你拥有的数据增大，只需对已有的数据做一些简单的变换。

我们说过，当向计算机输入一个图片，它得到的是像素值矩阵。假如这个矩阵的数字全部向左偏移一位，对人类来说，这个变化是难以觉察出来的。但是，对于计算机，这个变化是相当大的：数据变了，但是数据对于的标签（label）没有变。

将一个数据进行改变，但是该数据对应的标签保持不变，这种方式称为“数据增强技术”（data augmentation techniques）。（Approaches that alter the training data in ways that change the array representation while keeping the label the same are known as data augmentation techniques.）。这是一种人为拓展已有数据集的方法。

常用的数据增强方法有：灰度（grayscales），水平翻转（horizontal flips），垂直翻转（vertical flips），随机裁剪（random crops），颜色抖动（color jitters），平移（translations），旋转（rotations）等等。。
通过将这些转换应用到已有的数据集上，你可以成倍增加数据。