一：卷积神经网络入门

deepLearning

本文翻译自Adit Deshpande的博客：
A Beginner's Guide To Understanding Convolutional Neural Networks

简介

“卷积神经网络”，尽管听起来像只是生物学和数学外加一点计算机科学的奇怪结合物，实际上它是目前计算机视觉领域最具影响的发明之一。卷积神经网络开始出名，始于2012年，Alex Krizhevsky使用这项技术将图片识别错误率从历史最好记录26%降低到15%（在当时是一个了不起的提升），并赢得当年的ImageNet competition冠军（计算机视觉领域的奥林匹克）。在那之后，许多公司将深度学习应用到各自的核心服务中：Facebook在（视频）分类算法中使用神经网络，Google则将之用于图片搜索，Amazon用来做商品推荐。。。。。。图片处理是神经网络最经典、最热门的应用场景。我们今天将讨论如何使用CNNs来做图片分类。

问题领域

Image classification（图像分类），即输入图片，输出分类结果（比如猫、狗）。对人类来说，这是我们来到这个世界上最先学习的技能，成人可以毫不费力的识别图像。我们能够快速的识别所处的环境和周围的物体。我们具备从知识储备中抽象出新模式，快速识别和区分不同的环境或图片，然而计算机却很难做到。

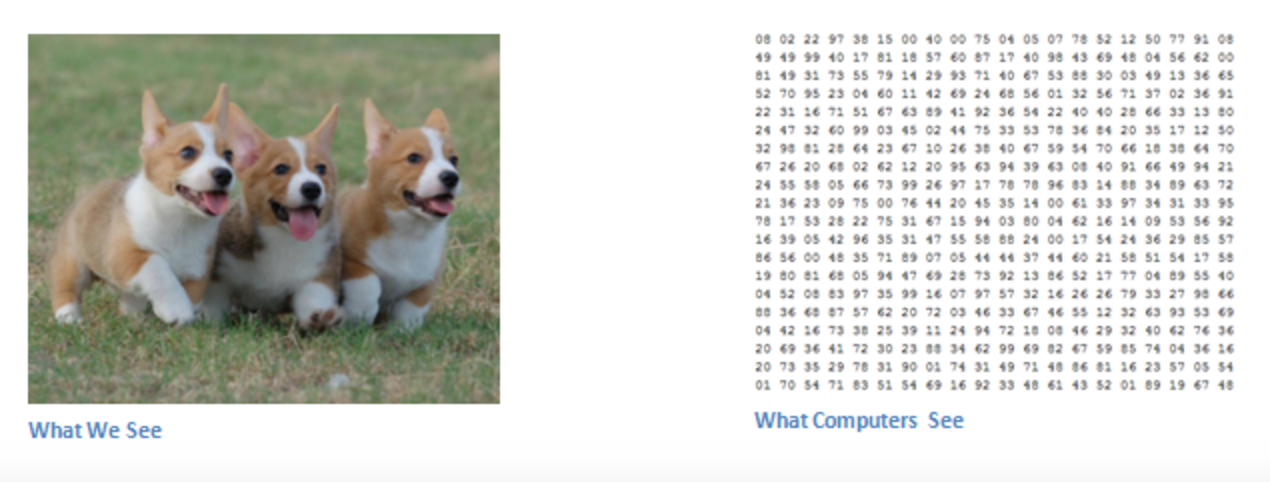
输入输出

对计算机输入一个图片，计算机看到的是一个像素值矩阵。假设图片像素值矩阵为32 x 32 x 3（3对应于RGB三色空间），如果是一个大小为480 x 480像素的彩色JPG图片，则它的像素值矩阵是480 x 480 x 3。代表每个像素的值，其取值范围为0～255，代表了色彩的深度。这些数值对人类看来毫无意义，但对计算机来说，是唯一能识别的输入。想法很简单：给计算机输入图片的数据矩阵，，让其输出图片内容是某个类别的概率有多大（比如80%是猫，15%是狗，5%是鸟）

我们希望计算机做什么

我们知道了要解决的问题，以及输入输出的形式，现在开始想想如何实现这个过程。我们希望计算机能够区分我们给它的不同图片，能够学习到狗／猫各自独有的特征。这个过程其实也在人类脑中下意识的发生：当我们看到一个狗的图片，我们会根据狗所具有的独特的爪子、4个脚等特征来判别这个图片里面是一只狗。相似的，计算机能够从识别“曲线、边界”等基本的图片特征开始，通过一系列的卷积层（convolutional layers）构建出上层抽象的特征（比如从曲线、边界等形状-->狗的脸）。这就是卷积神经网络（CNNs，convolutional neural network）基本的工作过程。

卷积神经网络（CNNs）和生物学的关系

卷积神经网络（CNNs）是受到生物视觉皮层工作原理的启发而发明的。生物视觉皮层里面有许多由神经细胞构成的感知区域，不同的感知区域负责感知不同的视觉对象。这个发现始于Hubel和Wiesel在1962的实验，他们发现人脑中的某些神经细胞，只感知某个特定方向的边缘形状（换句话说，只有某个特定方向的形状能够激发这些神经细胞）。比如，一些神经元能够感知垂直的边缘形状（vertical edges），一些能够感知水平或者对角边缘形状（horizontal or diagonal edges）。Hubel和Wiesel还发现，这些不同的神经元以柱状结构组合起来（organized in a columnar architecture），从而具备视觉感知能力。将系统分解为多个不同的专业组件处理专门的任务（比如，不同的神经元组识别不同的视觉特征），这样的思想是CNNs背后的原理。

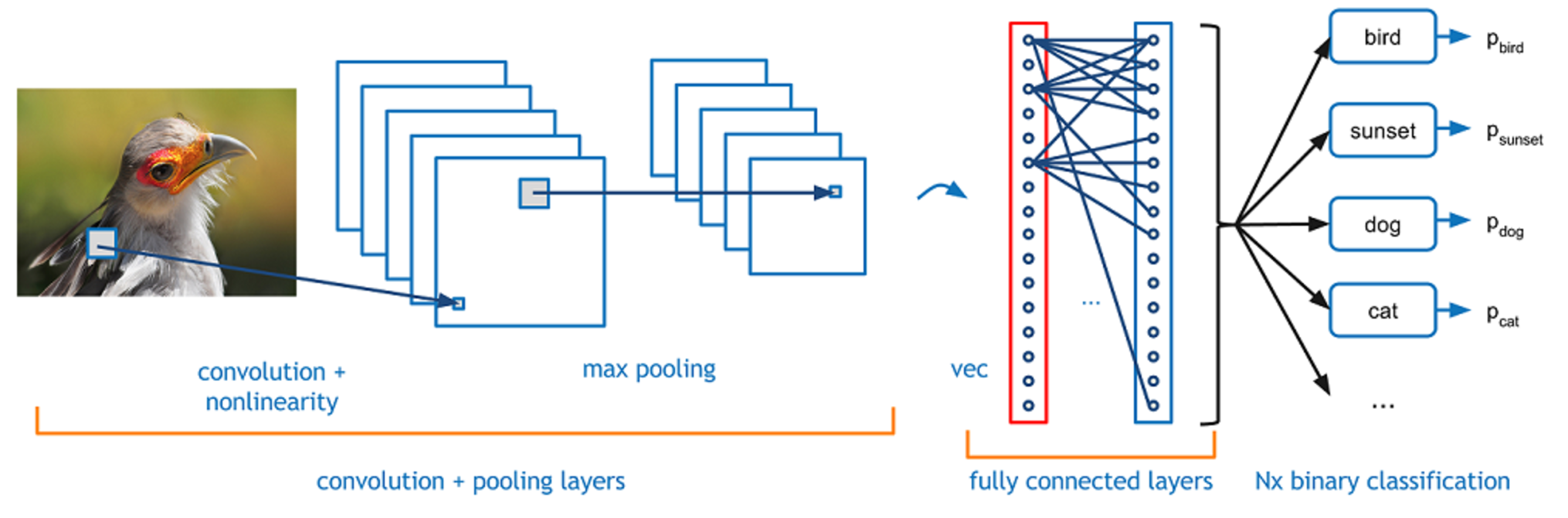
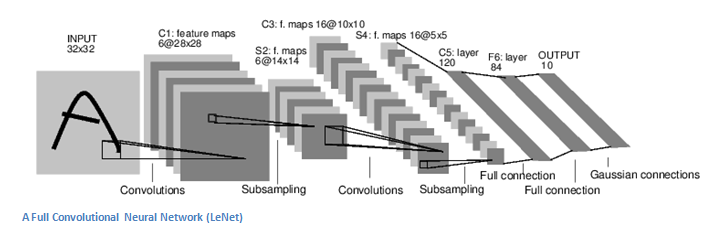
CNNs结构

回到细节问题。一个卷积神经网络，首先接受一个图片作为输入，接着经过“卷积层”（convolutional layer）、“非线性层”（nonlinear layer）、“池化层”（pooling layer，用于向下采样downsampling）和“全链接层”（fully connected layer），然后输出结果。结果可以是一个类别，或者输出所有类别和每个类别和图片的匹配程度。下面来逐层分析每一个layer。

第一层——从数学讲起

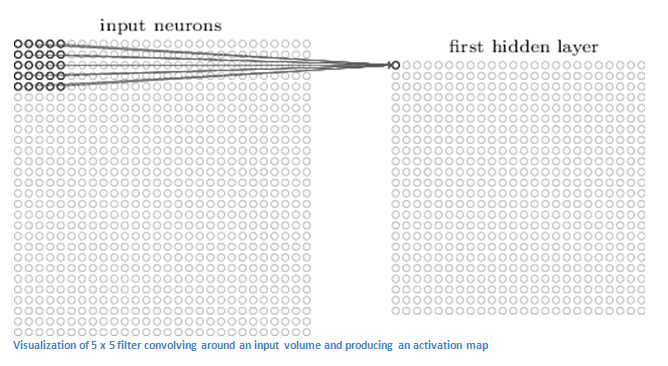
CNN的第一层是一个卷积层（Convolutional Layer）。假如我们的输入是32 x 32 x 3的像素值矩阵，现在假设你的眼光每次只能看到一个5x5大小的区域，你那这个5x5的区域从左往右、由上往下去扫描32x32矩阵。这个5x5矩阵就叫滤镜（filter，有时候也叫neuron［神经元］或者kernel）。而被filter扫描的图片区域称为“感知区域”（receptive field），对应于每次5x5扫描，每次的感知区域也是5x5的区域。filter本身是一个5x5的数值矩阵，这些数值被称为“权重”（weights）或者“参数”（parameters）。filter每扫描一块感知区域，会把感知区域的数值和filter的数值做一次“元素乘法”(element wise multiplication)，即把filter和感知区域对应位置的数值两两相乘，得到一个5x5的结果矩阵，然后把这个结果矩阵里面的所有数值（25个）加起来得到一个数值，这个数值代表了这块感知区域，并且这个值作为这个感知区域的卷积结果输出到一个隐层中（hidden layer），这个隐层也叫“卷积特征”或者“激活图”（‘Convolved Feature’ or ‘Activation Map’ ）。假如每次扫描，filter往前移动一位，随着filter依次扫描，最终得出一个新的矩阵，大小为28x28。而每次移动一位，这个称为“步长”（stride）为1。
承上，如果我们对32x32x3的3张通道分别用3个filter卷积一次，则可以得出28x28x3的数据。如果我们使用更多的filter，比如每个通道分别用2个filter，那么总共得出28x28x6的特征图。所以，输入一个特定的原始图，一次卷积得出来的特征图的个数，取决于神经元（即filter）的个数，这里把filter的个数称为“深度”（depth），如上面举的例子，深度分别是3和6。
上述讲了卷积层（convolutional layer）所做的事情。

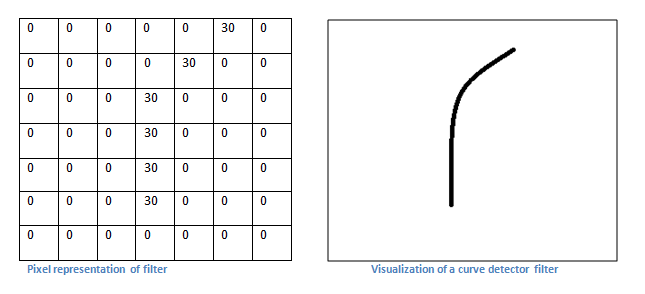
第一层——更抽象一些讲

现在，我们从更高层次理解卷积所做的事情。每个神经元（filter／neuron）都是一个特征识别器（feature identifier）。这里所讲的“特征”，指的是类似“直线”、“简单颜色”、“曲线”等等，这些所有图片都具有的特征。下面给出一个7x7x3的曲线检测器（a curve detector），为了方便，我们忽略3这个深度，只讲一个filter的情形。下图左边是一个曲线的像素值矩阵，右边是其对应的图像。我们的filter就是这个7x7的像素值矩阵。

现在我们把上面的filter应用到下面老鼠的图片中，从图片的左上角开始。

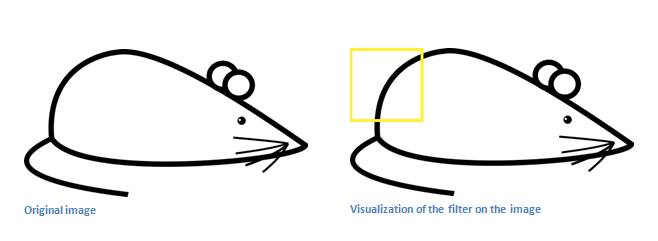
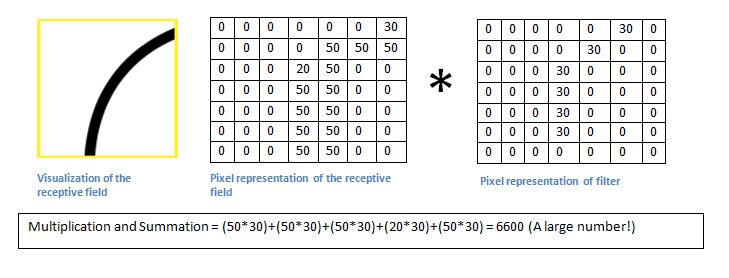
记住，卷积就是将filter和其对应的感知区域(receptive field)做元素乘法后将每个值相加。如下图所示，对图片左上角区域进行卷积，得到6600。这个值还是比较大的。实际上，如果感知区域的形状和filter比较相似，卷积后都会得到一个比较大的数值。

现在看看，如果是下面这种情况呢：

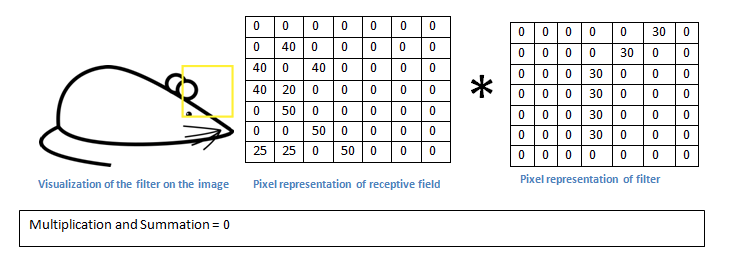
卷积的结果是0，这是因为感知区域内的图像形状和filter完全不同。我们知道卷积层（convolutional layer）就是激活图（activation map）。所以在上面的例子，激活图将展示出图片中出现的和filter中指定的曲线相似的区域。比如左上方第一个感知区卷积的值为6600，这么大的数字表明了感知区域内的图形，很大程度就是神经元（filter／neuron）需要检测的图形（换一句话说，神经元被这个区域激活了）。相反的，右上方第一个感知区域，我们的到的卷积值为0，这说明感知区域内没有神经元（filter／neuron）要检测的图形，即神经元在该区域没有被激活。这仅仅是一个神经元的情况，我们可以有多个filter来检测不同的形状，比如直角、圆圈等，越多的filter，则可以得到越多的激活图（activation map），从原始图片提取的特征和信息就越多。

在这一节里讨论的内容，只是拿一个最简单的例子来分析“卷积”过程所涉及的数学处理。下面的图片则是一个真实的神经网络在第一层卷积时，所用到的滤镜。

（该资料来自Stanford's CS 231N course，教师是Andrej Karpathy 和 Justin Johnson，裂墙推荐去看一下这个课程，对CNNs进一步了解）

继续探究

在常见的卷积神经网络架构中，在卷积层与卷积层之间会插入一些其它层。这些层具有各种作用，强烈建议你自己去深入了解。不过，通常，这些层提供了非线性（nonlinearities）、纬度保持（preservation of dimension）等功能，用于提高神经网络的健壮性（robustness），以及控制过度拟合（control overfitting）。一个经典的CNN架构如下：

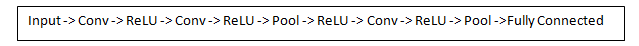
最后一层（FC层，Fully Connected Layer），是一个重要的一对一层，稍后我们将深入了解。现在回到第一个卷积层，第一个卷积层的filters用于检测最基本和底层的特征，比如边界、曲线等。但是为了能够判定图片内容是哪个物体，神经网络需要识别像“爪子”、“手”、“耳朵”等这些高层级的特征。
首先我们看一下第一次卷积后的结果：一个28x28x3的数据（假设对RGB三通道的3个数据矩阵分别施加一个5x5x3的filter做卷积）。这个结果是一个激活图（Activation Map）。
当我们对上面第一次卷积的结果，作为input输入到第二次卷积中，则得到二次卷积结果。这时候卷积结果已经难以可视化了（visualization）。
回到第一层卷积的输入，我们输入的是一个原始图片的像素值矩阵，进过第一层的卷积后，第二层卷积的输入变为第层卷积输出的激活图（Activation Map）。所以每一层次的输入实际上是对“原始图片中各种低层次特征所在的位置”的描述。
现在你在第二卷积层的输出处，再加上一批filter做卷积，可以得到更加高级别特征的激活图。比如“半圆”（一些曲线和直边的组合物）、“方形”（多个直边的组合）等。
随着卷积神经网络往下走，继续卷积，将得到越来越复杂特征的激活图。最后，你的filter可能就是一些能够被手写字激活的神经元，或者只能被粉红物件激活的神经元，等等。
最后，关于CNNs中的可视化滤镜（visualizing filters）课题，Matt Zeiler和Rob Fergus有专门的论文发表，Jason Yosinski还在YouTube上有视频讲解。
另外一件有趣的事，随着卷积神经网络往下走，filters的感知域（receptive field）越来越大，就是他们能够感知原始图片中较大块区域的信息。

全链接层（Fully Connected Layer）

经过了多个卷积层，现在我们能够检测高级别的特征。那么，来到最后一层了，这是一个“全链接层”。这一层的输入是前一层的输出（前一层可能是一个卷积层，或者一个ReLU，亦或者一个池化层［Pool layer］）。这一层的输出则是一个N维向量，N是需要区分的类别数。比如，你需要识别0～9的手写数字，那么N就是10个阿拉伯数字，输出结果是[0 .1 .1 .75 0 0 0 0 0 .05]，这说明输入的图片有0%的概率是0，10%的概率是1，75%的概率是3（其实还有其它很多种输出的形式，这里只是举个简单例子）。
全联接层做的事情是，检视上一层的输出（如我们前面所说的，这些输出是高层次特征的激活图），判定这些特征和各个类别的相关性。比如程序将一个图判定为“狗”，那么在“爪子”、“4条腿”等高级特征的激活图的数据必定比较大（表示激活程度高）｛If the program is predicting that some image is a dog, it will have high values in the activation maps that represent high level features like a paw or 4 legs, etc. ｝。
基本上，FC层检视高级别的特征，根据这些特征和某个类别的相关性，给每个特征以不同权重，从而根据上层输出的高级特征综合判定图像内容是某个类别的概率。

训练（通过训练使得整个神经网络运作）

训练是神经网络几乎最重要的部分。
你可能会有这样的疑问：第一卷积层的神经元（filter/neuron）是怎么知道检测边界和曲线的？全链接层是怎么知道需要检测什么激活图的？每个卷积层的神经元值（filter／neuron）是如何确定的？计算机是通过“反向传播”（backpropagation）来不断调整神经元的值的。
在开始讲反向传播之前，我们先讨论一下神经网络工作需要哪些东西。我们刚出生的时候，我们不知道什么是猫、狗或者鸟。同样的，在CNN开始运行前，各项权重（weights）和神经元的值是随机的。这些神经元不知道要去检测边线和曲线。在高层，这些随机生成的神经元也不知道要去检测爪子和鸟喙。
当我们不断成长，我们的父母和老师会教我们看不同的物体和图片，告诉我们这些东西分别是什么（给每个东西一个标签），这个过程就是CNNs训练的过程。在深入了解前，假设我们拥有一个训练集合，包含了成千上万的图片，包括猫、狗、鸟等等，每个图片都有一个标签，表示这个图片是什么动物。
那么我们如何教会CNNs去识别图片呢？通过反向传播让CNNs不断调整参数，以便最终识别图片。
反向传播包括4个部分：the forward pass（正向）， the loss function（损失函数）， the backward pass（反向）， the weight update（权重更新）
The forward pass：在这个过程中，如前面例子，我们将原始图片以32x32x3输入到CNNs中，让其从前往后经过整个CNNs的处理，在这一次中，由于所有的权重／神经元的值都是随机的，最终输出的结果可能是[.1 .1 .1 .1 .1 .1 .1 .1 .1 .1]，根本无法判别输入的图片是什么数字。这个阶段，神经网络根本无法判别数字，其每一层的神经元也不具备抽取特征的能力。那么是时候进入到下一步：The loss function
The loss function： 还记得我们具有一个带标签的图片集合？在给CNNs输入一个图片时，我们是知道这个图实际上代表什么数字的。比如给CNNs输入一个3的图片，那么我们期望CNNs能够输出[0 0 0 1 0 0 0 0 0 0]。损失函数可以有多个数学表达式，我们这里取一个最常用的，叫MSE（mean squared error，均方误差）：

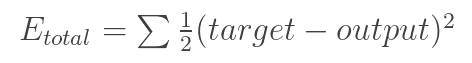
显然，我们运行CNNs第一次输出的预测值和真实值间误差是极大的。那如何降低这个误差的值？这是一个数学问题。
假设误差为L，神经网络中只有W1，W2两个权重参数（weight／neuron），假设画成坐标图如下：

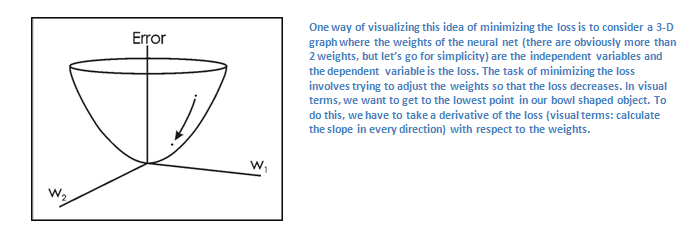
我们现在需要找出哪些参数（W1，W2）对误差L的贡献最大，这个过程就是求导dL/dW，W是神经网络中的权重参数（weight/neuron），通过这种反向过程back pass，我们找出对误差贡献最大的参数并调整其值（the weight update），使得误差不断减小。我们通过求最大梯度，然后往梯度的相反反向去调整参数，可以快速降低误差值。下图中，dL/dW是最大梯度值，η数学上来讲是梯度下降的速度参数，表示顺着最大梯度相反方向迈进的步长。在一开始的时候，由人工给其赋值，在这里我们称为“Learning Rate”。

Learning Rate这个值的大小的选定，也是一门学问，选的比较大，则训练的时间会缩短，但是一个太大的数值，会导致无法靠近最优点（即无法将误差降到靠近最低的点），如下图：

这样通过forward pass, loss function, backward pass, ，parameter update四个步骤，达成一轮训练。然后再开始新的一轮，如此往复，当完成训练集中的所有样本的训练，这个时候你的神经网络应该足够强大了。

测试

训练完CNNs，我们要验证它是否能工作。我们需要另外一个带标签的数据集合来测试它。（记住这个测试数据集合一定不能从训练数据集合中取，这样才有意义）。

商业公司如何使用CNNs

数据、数据、数据，重要事情说三遍，拥有数据的公司先天就已经获得一大截优势了。有越多的训练数据，则CNNs中参数的调优次数就越大，也越有效越精准，这样CNNs的效果会越好。Facebook和Instagram拥有大量图片数据，Google则坐拥搜索相关的数据，Amazon每天有成千上万的商品数据。。。现在你终于知道这些公司是如何使用这些数据的了。

未介绍到的内容

到这里，我们没有讨论的点有：
非线性层（nonlinear layer）和池化层（pooling layer）
神经网络的超级参数：比如神经元的大小（size of filter/neuron），卷积的步长（stride），零填充（zero padding）的大小等
神经网络的架构（network architecture）, 批标准化（BN，batch normalization）, 梯度消失（vanishing gradients）, dropout（dropout是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃，为了防止过度拟合）, initialization techniques, non-convex optimization,biases, choices of loss functions, data augmentation,regularization methods, computational considerations, modifications of backpropagation, and more were also not discussed.