L - Subway 题解

算法 题解

题目大意

一个无向图，有n n (3 ≤ n ≤ 3000) 个点，有且只有一个环，求各个点（包括环上的点）到环的最短距离。

分析

由于只有一个环，我们可以用DFS(深度优先搜索)进行环的判定。而且，任何点在DFS中遇到的第一个环上的点就是环上离这个点最近的点。而我们在DFS中需要一个vis数组进行标记，我们可以让vis数组还记录下走过的步数，即下代码中的step数组。注意步数不能从0开始计数，否则无法区分该点是否被vis。
下图便是这个图的一个例子：

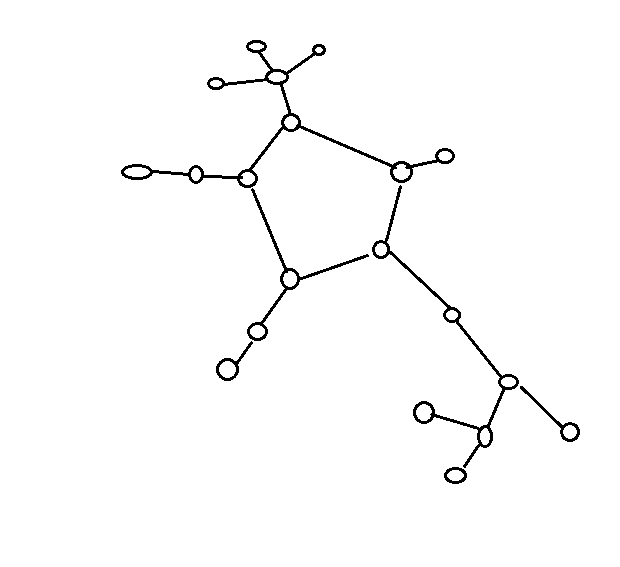
代码

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
    vector <int> pic[3005];
    int n;
    int step[3005];
int solve(int v,int fa,int s)
{
    step[v]=s;
    int i;
    for(i=0;i<pic[v].size();i++)
    {
        int u=pic[v][i];
        if(u==fa)
            continue;
        if(step[u])
            return step[u];
        int ans=solve(u,v,s+1);
        if(ans)
            return ans;
    }
    return 0;
}
int main(void)
{
    cin>>n;
    int i;
    for(i=0;i<n;i++)
    {
        int u,v;
        cin>>u>>v;
        pic[u].push_back(v);
        pic[v].push_back(u);
    }
    for(i=1;i<=n;i++)
    {
        memset(step,0,sizeof(step));
        if(i!=1)
            cout<<" ";
        cout<<solve(i,-1,1)-1;
    }
    return 0;
}