支持向量机

Kernel

---

二分类

硬间隔支持向量机

支持向量机很早很早就被提出来了，而且在最近几年里一直在被更新和改进，但是追本溯源，我们还是得回到那个古老的年代，去看看支持向量机原本的模样。

我们总是希望这世界上的事情没有那么多的弯弯绕绕，能一刀切开就好了。SVM 最早干的就是这一刀切的工作。现在有两拨样本，标签分别是 $\left\{-1,+1\right\}$，它们在原空间上的分布如下图所示：

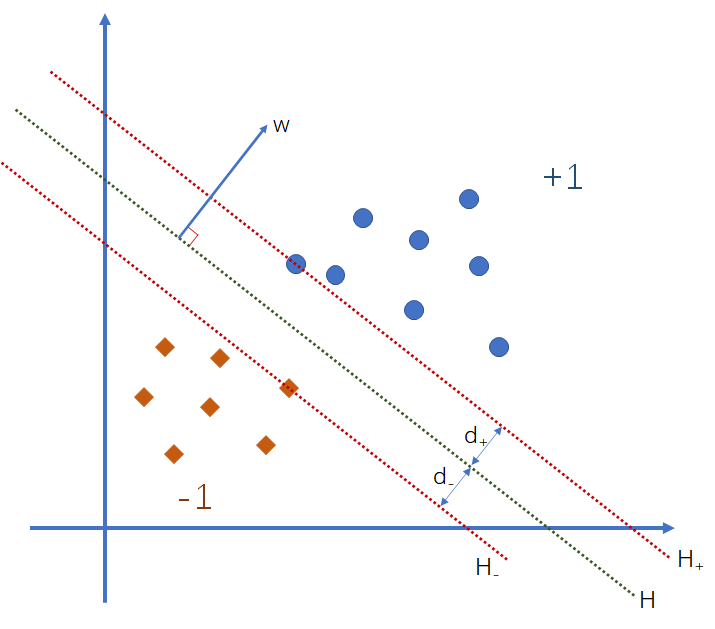
我们希望能够找到一条分界线，把两拨样本合理地分开，而且尽可能地让最靠近分解的样本点之间的距离最大，也就是图中的 $d_+$ 与 $d_-$ 之和要最大。当我们确定分界线之后，无论类别是什么，我们取最靠近分界线的样本点，做穿过该样本点且与分界线平行的直线，称之为边界线，两个类别的边界线距离就是间隔(Margin)。我们给图中的线 $H$ 定义一个方程，即：

$$w^Tx+b=0$$ 而 $H_+$ 和 $H_-$ 则分别是

$$\left\{ \begin{array}{ll} w^Tx+b=1 \\ w^Tx+b=-1 \end{array} \right.$$

我们合并这两个边界线的方程，即：

$$y_i(w^Tx_i+b)\geq1\quad\quad \left\{ \begin{array}{ll} \forall i\in 1,\cdots,N \\ \forall y_i\in\left\{-1,+1\right\} \end{array} \right.$$

那我们会开始思考，既然我是想要让间隔最大，那我应该考虑间隔是什么，于是这里就要用到高中学的一个知识点——两直线间的距离公式：

$$D=\frac{|c_1-c_2|}{\sqrt{A^2+B^2}}$$ 由于 $H_-$ 到 $H$ 的距离和 $H_+$ 到 $H$ 的距离势必要相等的，因此间隔就是：

$$\begin{array}{l} D&=D(H_-,H)+D(H_+,H) \\ &=\frac{|b-(b+1)|}{\sqrt{(w^T)^2}}+\frac{|b-(b-1)|}{\sqrt{(w^T)^2}} \\ &=\frac{1}{||w||}+\frac{1}{||w||} \\ &=\frac{2}{||w||}=\frac{2}{\sqrt{w^Tw}}\tag{1} \end{array}$$

在式 $(1)$ 中，我们能发现如果希望 $D$ 越大，那必须让 $w^Tw$ 越小，因此这就转换成一个最优化问题，求的是 $w^Tw$ 的最小值，当然还有一个限制条件，就是要限制样本点不能出现在间隔当中，只能是在间隔边上或者间隔外，即：

$$\begin{array}{l} minimize\quad \Phi(w)=\frac{1}{2}w^Tw \\ subject.to\quad y_i(w^Tx_i+b)\geq1\quad\forall i\in1,\cdots,N \end{array}$$

接着我们得构造 $\Phi(w)$ 的拉格朗日多项式，要先做个说明的是，为什么是减号，而不是加号：

$$\begin{array}{l} y_i(w^Tx_i+b)\geq1\\ 1-y_i(w^Tx_i+b)\leq0\\ -y_i(w^Tx_i+b)+1\leq0 \end{array}$$

说明结束，转换成拉格朗日多项式就是

$$L(w,b,\alpha)=\frac{1}{2}w^Tw-\sum_{i=1}^N\alpha_i[y_i(w^Tx_i+b)-1]$$

接着对 $w$ 和 $b$ 做微分：

$$\begin{array}{l} \frac{\partial L}{\partial w}=0\Rightarrow w=\sum_{i=1}^N\alpha_iy_ix_i \\ \frac{\partial L}{\partial b}=0\Rightarrow \sum_{i=1}^N\alpha_iy_i=0 \end{array}$$

那这样子我们就能求出在原空间中的 $L(w,b,\alpha)$ 是个啥了。将拉格朗日多项式的微分所得带回 $L$ 中，但我们可以先算 $w^Tw$ 和 $w^Tx_i$ 即：

$$\begin{array}{l} w^Tw&=(\sum_{i=1}^N\alpha_iy_ix_i^T)(\sum_{j=1}^N\alpha_jy_jx_j) \\ &=\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j \\ w^Tx_i&=(\sum_{j=1}^N\alpha_jy_jx_j^T)x_i \\ &=\sum_{j=1}^N\alpha_jy_jx_j^Tx_i \end{array}$$

接着我们把上面两结果带进 $L(w,b,\alpha)$ 里，可得：

$$\begin{array}{l} W(\alpha)=L(w(\alpha),b(\alpha),\alpha)&=\frac{1}{2}w^Tw-\sum_{i=1}^N\alpha_i[y_i(w^Tx_i+b)-1] \\ &=\frac{1}{2}w^Tw-\sum_{i=1}^N\alpha_iy_iw^Tx_i-b\sum_{i=1}^N\alpha_iy_i+\sum_{i=1}^N\alpha_i \\ &=\frac{1}{2}w^Tw-\sum_{i=1}^N\alpha_iy_iw^Tx_i+\sum_{i=1}^N\alpha_i \\ &=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j-\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j+\sum_{i=1}^N\alpha_i \\ &=\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jx_i^Tx_j \end{array}$$

到这里，我们可算是把 $W(\alpha)$ 给整出来了，于是乎我们就转换成了一个对偶问题，来求 $W(\alpha)$ 的最大值，但是要记得它有俩限制式：

$$\begin{array}{l} (1)\quad\quad\sum_{i=1}^N\alpha_iy_i=0 \\ (2)\quad\quad\alpha_i\geq0\quad\forall i=1,\cdots,N \end{array}$$

到这里，我们对于原空间的推导就结束了，因为我们的主要目的是把它映射到高维空间去，也就是把全部的 $x_i$ 都换成 $\phi(x_i)$，推导过程和在原空间时是一致的，只不过是把 $w^Tx_i$ 换成了 $w^T\phi(x_i)$，即：

$$\begin{array}{l} W(\alpha)=L(w(\alpha),b(\alpha),\alpha)&=\frac{1}{2}w^Tw-\sum_{i=1}^N\alpha_i[y_i(w^T\phi(x_i)+b)-1] \\ &=\frac{1}{2}w^Tw-\sum_{i=1}^N\alpha_iy_iw^T\phi(x_i)-b\sum_{i=1}^N\alpha_iy_i+\sum_{i=1}^N\alpha_i \\ &=\frac{1}{2}w^Tw-\sum_{i=1}^N\alpha_iy_iw^T\phi(x_i)+\sum_{i=1}^N\alpha_i \\ &=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)-\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)+\sum_{i=1}^N\alpha_i \\ &=\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j) \\ &=\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\kappa(x_i,x_j) \end{array}$$

接着通过 KKT 来对 $\alpha^*$ 做分析，我们会发现当 $\alpha_i^*>0$ 时，因为 $\alpha_i^*[y_i(w^{*T}+\phi(x_i)+b^*)-1]=0$，所以 $y_i(w^{*T}+\phi(x_i)+b^*)=1$，那样本点刚好就落在边界线上；如果 $y_i(w^{*T}+\phi(x_i)+b^*)>1$，则意味着 $\alpha_i^*=0$ ，换句话说，当 $\alpha_i^*=0$ 时，该样本点处于间隔之外。

于是我们就能确定:

$$w=\sum_{\alpha_i^*≠0}\alpha_i^*y_i\phi(x_i)$$

$$b^*=y_t-w^{*T}\phi(x_i)=y_t-\sum_{i=1}^N\alpha_i^*\kappa(x_i,x_j)$$

最终得到最后的分界线方程就是：

$$y_{new}=sign(\sum_{i=1}^N\alpha_iy_i\kappa(x_i,x_{new})+b)$$

软间隔支持向量机

原始优化问题：

$$Minimize\quad\quad\phi(w,\xi)=\frac{1}{2}w^Tw+C\sum_{i=1}^l\xi_i,\quad C>0$$

$$Subject\quad to\quad\xi\geq0,\quad y_i(w^Tx_i+b)\geq1-\xi,\quad\forall i=1,\cdots,l$$

构造拉格朗日方程：

$$Minimize\quad\quad L(w,b,\xi,\alpha,\beta)=\frac{1}{2}w^Tw+C\sum_{i=1}^l\xi_i-\sum_{i=1}^l\alpha_i[y_i(w^Tx_i+b)-1+\xi_i]-\sum_{i=1}^l\beta_i\xi_i$$

$$Subject\quad to\quad\alpha_i,\beta_i\geq0\quad\forall i=1,\cdots\,l$$

分别对$w,b,\xi_i$做微分：

$$\frac{\partial L(w,b,\xi,\alpha,\beta)}{\partial w}=0\Rightarrow\sum_{i=1}^l\alpha_iy_ix_i$$

$$\frac{\partial L(w,b,\xi,\alpha,\beta)}{\partial b}=0\Rightarrow\sum_{i=1}^l\alpha_iy_i=0$$

$$\frac{\partial L(w,b,\xi,\alpha,\beta)}{\partial \xi_i}=0\Rightarrow C-\alpha_i-\beta_i=0\Rightarrow \left\{ \begin{array}{ll} \alpha_i=C-\beta_i&\\ \beta_i=C-\alpha_i& \end{array} \right. \Rightarrow0\leq\alpha_i,\beta_i\leq C$$

很明显，在这之前我们对原空间进行计算，现在我们要将$x_i$投射到高维空间，于是所有的$x_i$都要变成$\phi(x_i)$

$$Minimize\quad\quad L(w,b,\xi,\alpha,\beta)=\frac{1}{2}w^Tw+C\sum_{i=1}^l\xi_i-\sum_{i=1}^l\alpha_i[y_i(w^T\phi(x_i)+b)-1+\xi_i]-\sum_{i=1}^l\beta_i\xi_i$$

$$Subject\quad to\quad\alpha_i,\beta_i\geq0\quad\forall i=1,\cdots\,l$$
分别对$w,b,\xi_i$做微分：

$$\begin{aligned} \frac{\partial L(w,b,\xi,\alpha,\beta)}{\partial w}=0\Rightarrow\sum_{i=1}^l\alpha_iy_i\phi{(x_i)} &=\left[ \begin{array}{ccc} \phi{(x_1)},\cdots,\phi{(x_l)} \end{array} \right] \left[ \begin{array}{ccc} \alpha_1y_1\\ \vdots\\ \alpha_l y_l \end{array} \right]\\ &=\left[ \begin{array}{ccc} \phi{(x_1)},\cdots,\phi{(x_l)} \end{array} \right] \left[ \begin{array}{ccc} y_1,\cdots,0\\ \vdots,\ddots,\vdots\\ 0,\cdots,y_l \end{array} \right] \left[ \begin{array}{ccc} \alpha_1\\ \vdots\\ \alpha_l \end{array} \right]\\ &=X^TY\alpha,\quad Y=diag(y_1,\cdots,y_l)\\ \frac{\partial L(w,b,\xi,\alpha,\beta)}{\partial b}=0\Rightarrow\sum_{i=1}^l\alpha_iy_i=0&=y^T\alpha\\ \frac{\partial L(w,b,\xi,\alpha,\beta)}{\partial \xi_i}=0\Rightarrow C-\alpha_i-\beta_i&=0\Rightarrow \left\{ \begin{array}{ll} \alpha_i=C-\beta_i&\\ \beta_i=C-\alpha_i& \end{array} \right. \Rightarrow0\leq\alpha_i,\beta_i\leq C \end{aligned}$$
$$\begin{aligned} w^Tw=(X^TY\alpha)^T(X^TY\alpha)=\alpha^TYXX^TY\alpha&=\alpha^TY \left[ \begin{array}{ccc} \phi{(x_1)}^T\\ \vdots\\ \phi{(x_l)}^T \end{array} \right] \left[ \begin{array}{ccc} \phi{(x_1)},\cdots,\phi{(x_l)} \end{array} \right] Y\alpha\\ &=\alpha^TY \left[ \begin{array}{ccc} \phi(x_1)^T\phi(x_1),\cdots,\phi(x_1)^T\phi(x_l)\\ \vdots\quad\quad,\ddots,\quad\quad\vdots\\ \phi(x_l)^T\phi(x_1),\cdots,\phi(x_l)^T\phi(x_l) \end{array} \right] Y\alpha\\ &=\alpha^TYKY\alpha\\ &=\sum_{i=1}^l\sum_{i=1}^l\alpha_i\alpha_jy_iy_j\kappa(x_i,x_j) \end{aligned}$$
$$\begin{aligned} w^T\phi(x_i)=(X^TY\alpha)^T\phi(x_i)=\alpha^TYX\phi(x_i)&=\alpha^TY \left[ \begin{array}{ccc} \phi{(x_1)}^T\\ \vdots\\ \phi{(x_l)}^T \end{array} \right]\phi(x_i)\\ &=\alpha^TY \left[ \begin{array}{ccc} \phi{(x_1)}^T\phi(x_i)\\ \vdots\\ \phi{(x_l)}^T\phi(x_i) \end{array} \right]\\ &=\alpha^TY \left[ \begin{array}{ccc} \kappa{(x_1,x_i)}\\ \vdots\\ \kappa{(x_l,x_i)} \end{array} \right]\\ &=\sum_{j=1}^l\alpha_jy_j\kappa(x_j,x_i) \end{aligned}$$
将拉格朗日等式展开，并代入上述结果，得：
$$\begin{aligned} W(\alpha)&=\frac{1}{2}w^Tw+C\sum_{i=1}^l\xi_i-\sum_{i=1}^l\alpha_i[y_i(w^T\phi(x_i)+b)-1+\xi_i]-\sum_{i=1}^l\beta_i\xi_i\\ &=\frac{1}{2}w^Tw+C\sum_{i=1}^l\xi_i-\sum_{i=1}^l\alpha_iy_iw^T\phi(x_i) -b\sum_{i=1}^l\alpha_iy_i+\sum_{i=1}^l\alpha_i-\sum_{i=1}^l\alpha_i\xi_i-\sum_{i=1}^l\beta_i\xi_i\\ &=\frac{1}{2}w^Tw+C\sum_{i=1}^l\xi_i-\sum_{i=1}^l\alpha_iy_iw^T\phi(x_i) +\sum_{i=1}^l\alpha_i-\sum_{i=1}^l(\alpha_i+\beta_i)\xi_i\\ &=\frac{1}{2}\alpha^TYKY\alpha+C\sum_{i=1}^l\xi_i-\sum_{i=1}^l\alpha_iy_i(\alpha^TYX\phi(x_i)) +\sum_{i=1}^l\alpha_i-\sum_{i=1}^lC\xi_i\\ &=\frac{1}{2}\alpha^TYKY\alpha-\alpha^TYX\sum_{i=1}^l\alpha_iy_i\phi(x_i)+\sum_{i=1}^l\alpha_i\\ &=\frac{1}{2}\alpha^TYKY\alpha-\alpha^TYX \left[ \begin{array}{ccc} \alpha_1\\ \vdots\\ \alpha_l \end{array} \right] \left[ \begin{array}{ccc} y_1,\cdots,0\\ \vdots,\ddots,\vdots\\ 0,\cdots,y_l \end{array} \right] \left[ \begin{array}{ccc} \phi{(x_1)},\cdots,\phi{(x_l)} \end{array} \right] +\sum_{i=1}^l\alpha_i\\ &=\frac{1}{2}\alpha^TYKY\alpha-\alpha^TYXX^TY\alpha+\sum_{i=1}^l\alpha_i\\ &=\frac{1}{2}\alpha^TYKY\alpha-\alpha^TYKY\alpha+\sum_{i=1}^l\alpha_i =\sum_{i=1}^l\alpha_i-\frac{1}{2}\alpha^TYKY\alpha \end{aligned}$$