@KirinBill
2018-03-27T12:42:15.000000Z
字数 18697
阅读 2609
DP优化——斜率优化
动态规划
目录
思想
- 在一些DP的题目中,朴素的DP方程往往需要枚举每一个之前可转移过来的状态来取最优转移,这在复杂度上是不允许的;
- 斜率优化就是通过将DP方程展开、化简形成一个形如的式子,其中是无论怎么决策都需要加上的东西,那其实可以拿到式子外面;
- 这样,如果把看做直线的斜率,看做直线的纵截距,那么之前的每个状态都可以看做是一个一次函数,也就是直线了;
- 把视为自变量,那么我们如果维护之前的形成的上/下凸壳(也就是极值或者最优决策集合),每次带入就可以迅速转移了;
- 这就是所谓的斜率优化——利用类似直线斜率的东西来优化DP转移复杂度;
- 我们以一道经典题为例看一下具体的操作:
例题:[HNOI 2008] 玩具装箱
- 考虑最朴素的DP方程:
- 对于那个,显然我们可以用前缀和优化一下(设),而我们还可以用一个小技巧:令,这样式子里面就没有除了的常数项,比较好看;
- 现在DP方程变为了:
- 注意到有一个形式相同的部分:,令其为;
- 接下来将式子完全展开并分为三部分:与都有关的,只与有关的,只与有关的(这部分拆到式子外面,与决策无关);
- 考虑到我们维护的凸壳就是最优决策集合,那么每次将当前的带入求出最小值后将代表的直线加入凸壳即可,如果维护凸壳的复杂度是的话总复杂度就降到了,因为转移由变成了;
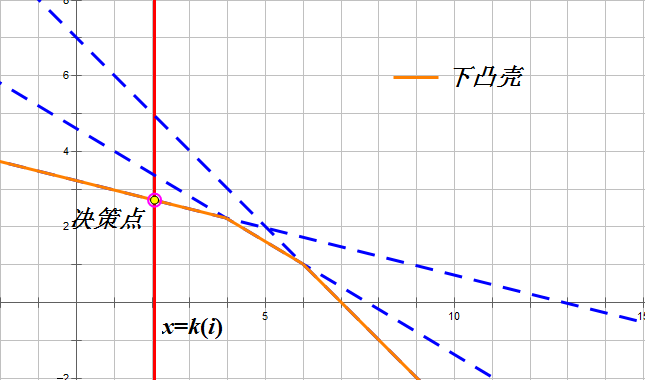
- 观察发现斜率是单调递减的(前缀和和下标都是单调递增的),画个图可以知道,我们维护的是下凸壳(维护上下凸壳应具体情况具体分析),每次只需要删之前斜率最小(斜率是负的,从队首到队尾大小单调递减)的那一些就可以了;
又由于自变量单调递增,我们可以用双端队列维护下凸壳,从队首到队尾斜率单调递减,具体过程如下:
- 如果自变量在直线与直线交点的右侧,说明直线以后都没有用了,可以弹出。实现的话比较一下和两个决策谁更优就好了;
- 加入的直线与直线的交点在直线与直线的交点左侧,则要弹出,因为它被顶到凸壳上面了;
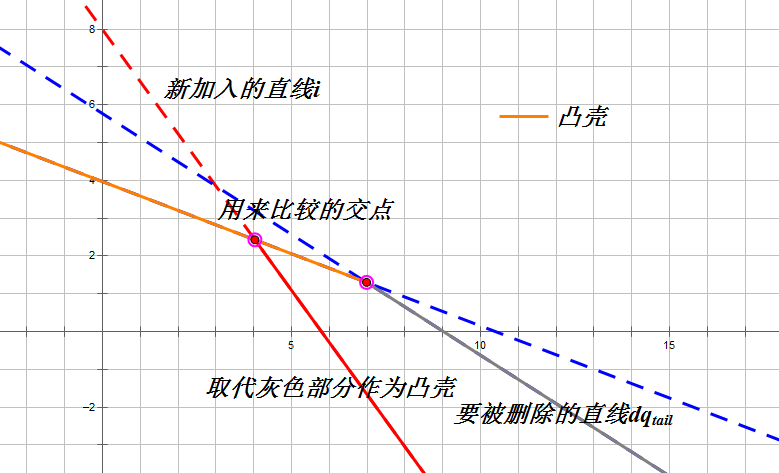
- 交点在右侧的话就不需要删除了;
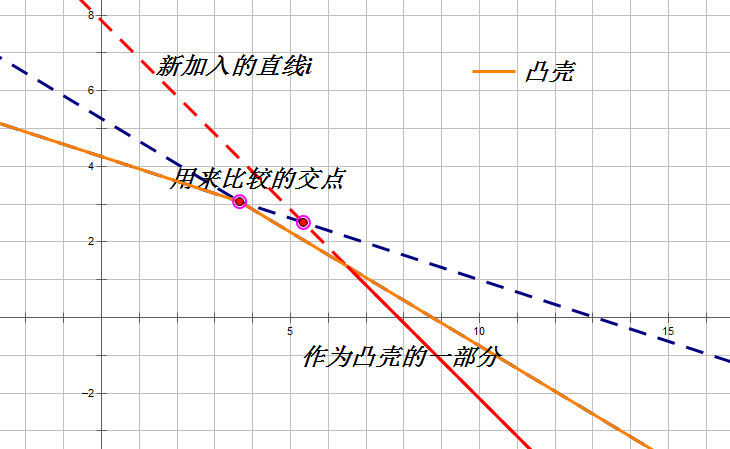
- 对于加入直线时具体弹哪种直线,具体问题画个图看一下就好了;
这样的话,维护凸壳的均摊复杂度就是的了,于是这题总复杂度就由降到了
代码:
#include <cstdio>const int MAXN=50005;int n,l;long long k[MAXN],dp[MAXN];inline long long sqr(register long long x){return x*x;}//interceptinline long long y_itcpt(int i){return sqr(k[i])+(l*k[i]<<1)+dp[i];}inline long long slope(int i){return -(k[i]<<1);}inline long long cal(int i,int j){return slope(j)*k[i]+y_itcpt(j);}//intersectioninline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];int head=0,tail=0;for(int i=1;i<=n;++i){while(head<tail && cal(i,dq[head])>=cal(i,dq[head+1]))++head;dp[i]=cal(i,dq[head])+sqr(k[i]-l);while(head<tail && itsct(i,dq[tail-1])<=itsct(dq[tail],dq[tail-1]))--tail;dq[++tail]=i;}return dp[n];}int main(){scanf("%d%d",&n,&l);++l;for(int i=1;i<=n;++i){scanf("%d",&k[i]);k[i]+=k[i-1];}for(int i=1;i<=n;++i)k[i]+=i;printf("%lld",slopeDP());return 0;}
练习
普通斜率优化
- 这题和例题有点像,但是考虑到不需要连续购买一段土地,我们需要先变一下形;
- 显然,若存在则一定和一起买最优,我们可以把这种都忽略掉;
- 而且,如果我们按照为第一关键字、为第二关键字排序,可以发现是升序的而是降序的(反证法易得若存在不满足这样的土地,意味着它一定是上述的那样的,已经忽略了);
- 现在贪心的想一下,如果我们在这个顺序下买不连续的一段一定不优。因为代价是,所以如果跳着,中间一个不影响的土地会被忽略,一定不比把它加进去一起买更优;
- 那么现在问题就是把序列分成若干段,每段的代价是,求最小代价和;
- 不难写出DP方程:
- 又有刚刚的性质可以得出最值,那么有,为直线的斜率,按照套路就切了。
代码:
#include <cstdio>#include <algorithm>using std::sort;const int MAXN=50005;int n;long long dp[MAXN];struct square{int a,b;static bool cmp_ab(const square &a,const square &b){return a.a<b.a || (a.a==b.a && a.b<b.b);}}field[MAXN],tmp[MAXN];inline int slope(int i){return field[i+1].b;}inline long long y_itcpt(int i){return dp[i];}inline long long cal(int i,int j){return (long long)slope(j)*field[i].a+y_itcpt(j);}inline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];int head=0,tail=0;for(int i=1;i<=n;++i){while(head<tail && cal(i,dq[head])>=cal(i,dq[head+1]))++head;dp[i]=cal(i,dq[head]);while(head<tail && itsct(i,dq[tail-1])<=itsct(dq[tail],dq[tail-1]))--tail;dq[++tail]=i;}return dp[n];}int main(){scanf("%d",&n);for(int i=1;i<=n;++i)scanf("%d%d",&tmp[i].a,&tmp[i].b);sort(tmp+1,tmp+n+1,square::cmp_ab);int cnt=0;for(int i=1;i<=n;++i){while(cnt && field[cnt].b<=tmp[i].b)--cnt;field[++cnt]=tmp[i];}n=cnt;printf("%lld",slopeDP());return 0;}
- 这题的话没法那么裸的用前缀和了,所以需要三个值到山脚的距离、物品个数前缀和以及带权物品个数前缀和;
- 那么:
代码:
#include <cstdio>const int MAXN=1000005;int n;int dis[MAXN],c[MAXN],p[MAXN];long long sum[MAXN],sum_dis[MAXN],dp[MAXN];inline long long slope(int i){return sum[i];}inline long long y_itcpt(int i){return dp[i]-sum_dis[i];}inline long long cal(int i,int j){return slope(j)*dis[i]+y_itcpt(j);}inline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];int head=0,tail=0;for(int i=1;i<=n;++i){while(head<tail && cal(i,dq[head])>=cal(i,dq[head+1]))++head;dp[i]=cal(i,dq[head])+c[i]-dis[i]*sum[i]+sum_dis[i];while(head<tail && itsct(i,dq[tail-1])>=itsct(dq[tail],dq[tail-1]))--tail;dq[++tail]=i;}return dp[n];}inline void pre_cal(){for(int i=1;i<=n;++i){dis[i]=dis[n]-dis[i];sum[i]=sum[i-1]+p[i];sum_dis[i]=sum_dis[i-1]+(long long)p[i]*dis[i];}}int main(){scanf("%d",&n);for(int i=1;i<=n;++i)scanf("%d%d%d",&dis[i],&p[i],&c[i]);pre_cal();printf("%lld",slopeDP());return 0;}
- 和上题几乎一样,不多说了。。。
- 设表示到的距离,那么,,
代码:
#include <cstdio>const int MAXN=1000005;int n;int a[MAXN],b[MAXN];long long sum[MAXN],sum_dis[MAXN],dp[MAXN];inline long long slope(int i){return sum[i];}inline long long y_itcpt(int i){return dp[i]-sum_dis[i];}inline long long cal(int i,int j){return slope(j)*(n-i)+y_itcpt(j);}inline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];int head=0,tail=0;for(int i=1;i<=n;++i){while(head<tail && cal(i,dq[head])>=cal(i,dq[head+1]))++head;dp[i]=cal(i,dq[head])+sum_dis[i]-(n-i)*sum[i]+a[i];while(head<tail && itsct(i,dq[tail-1])>=itsct(dq[tail],dq[tail-1]))--tail;dq[++tail]=i;}return dp[n];}inline void pre_cal(){for(int i=1;i<=n;++i){sum[i]=sum[i-1]+b[i];sum_dis[i]=sum_dis[i-1]+(long long)(n-i)*b[i];}}int main(){scanf("%d",&n);for(int i=1;i<=n;++i)scanf("%d",&a[i]);for(int i=1;i<=n;++i)scanf("%d",&b[i]);pre_cal();printf("%lld",slopeDP());return 0;}
- 这题就是上面两题的简化版。。。
- 设为到的距离,,那么:
代码:
#include <cstdio>const int MAXN=1e6+5;int n;int a[MAXN];long long dp[MAXN];inline long long sqr(register long long x){return x*x;}inline int slope(int i){return -i;}inline long long y_itcpt(int i){return dp[i]+(sqr(i)+i>>1);}inline long long cal(int i,int j){return (long long)slope(j)*i+y_itcpt(j);}inline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];int head=0,tail=0;for(int i=1;i<=n;++i){while(head<tail && cal(i,dq[head])>=cal(i,dq[head+1]))++head;dp[i]=cal(i,dq[head])+(sqr(i)-i>>1)+a[i];while(head<tail && itsct(i,dq[tail-1])<=itsct(dq[tail],dq[tail-1]))--tail;dq[++tail]=i;}return dp[n];}int main(){scanf("%d",&n);for(int i=1;i<=n;++i)scanf("%d",&a[i]);printf("%lld",slopeDP());return 0;}
- 这题和例题十分相像,就不多说了;
- DP方程为(为前缀和):
代码:
#include <cstdio>const int MAXN=1000005;int n,a,b,c;int sum[MAXN];long long dp[MAXN];inline long long sqr(register long long x){return x*x;}inline long long slope(int i){return (long long)-(a<<1)*sum[i];}inline long long y_itcpt(int i){return dp[i]+a*sqr(sum[i])-(long long)b*sum[i];}inline long long cal(int i,int j){return slope(j)*sum[i]+y_itcpt(j);}inline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];int head=0,tail=0;for(int i=1;i<=n;++i){while(head<tail && cal(i,dq[head])<=cal(i,dq[head+1]))++head;dp[i]=cal(i,dq[head])+a*sqr(sum[i])+(long long)b*sum[i]+c;while(head<tail && itsct(i,dq[tail-1])<=itsct(dq[tail],dq[tail-1]))--tail;dq[++tail]=i;}return dp[n];}int main(){scanf("%d",&n);scanf("%d%d%d",&a,&b,&c);for(int i=1;i<=n;++i){scanf("%d",&sum[i]);sum[i]+=sum[i-1];}printf("%lld",slopeDP());return 0;}
- SD真是个数学强省Orz
- 考虑到直接按方差定义式是不可做的(DP的话不可能从前个的平均数怎么一下转移到前个),我们变形一下(为什么有神佬说这是初中数学公式,本蒟蒻根本没学过...):
- 所以,这题其实是要最小化,那么很容易得到DP方程:
- 而且有个细节,就是从转移到时会挂掉,因为前个数分段,这根本就不存在,所以应该先求出所有,从开始DP,而且要注意,这里的双端队列其实放的是所代表的直线,所以每层DP前应该在双端队列里加入一个。
代码:
#include <cstdio>const int MAXN=3005;int n,m;int sum[MAXN];long long dp[MAXN][MAXN];inline long long sqr(register long long x){return x*x;}inline long long slope(int i){return -(sum[i]<<1);}inline long long y_itcpt(int i,int k){return dp[k][i]+sqr(sum[i]);}inline long long cal(int i,int j,int k){return slope(j)*sum[i]+y_itcpt(j,k);}inline double itsct(int i,int j,int k){return (double)(y_itcpt(j,k)-y_itcpt(i,k))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];for(int i=1;i<=n;++i)dp[1][i]=sqr(sum[i]);for(int i=2,head,tail;i<=m;++i){head=tail=0,dq[0]=i-1;for(int j=i;j<=n;++j){while(head<tail && cal(j,dq[head],i-1)>=cal(j,dq[head+1],i-1))++head;dp[i][j]=cal(j,dq[head],i-1)+sqr(sum[j]);while(head<tail && itsct(j,dq[tail-1],i-1)<=itsct(dq[tail],dq[tail-1],i-1))--tail;dq[++tail]=j;}}return m*dp[m][n]-sqr(sum[n]);}int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;++i){scanf("%d",&sum[i]);sum[i]+=sum[i-1];}printf("%lld",slopeDP());return 0;}
- 这题我们还考虑像上一题一样,设为前个进行了次操作的最大价值,但是乍一看,即使我们确定了分割点,不同的操作顺序也会影响答案,这就没法像之前那样DP了;
- 其实不然,考虑一下每次分割时的价值代表什么:分割开的两边的元素两两配对,产生的价值是它们的值的乘积。那么只要分割点确定了,产生的价值就确定了,与操作顺序无关;
- 那么有:
- 而且和上题不同的是,确实都是,因为不操作就是没有价值,所以直接DP就可以了;
- 但是这题卡空间,而每次转移只要上一层的DP值,所以开滚动数组好了;
- 有一点需要注意一下,就是这题的序列值可能为,那么不是单调递增了,只是单调不降了,所以会有加入平行直线的情况,这时需要特判一下,具体操作如下:
- 按照正常的操作弹出的直线,因为这时的判断仍然是对的;
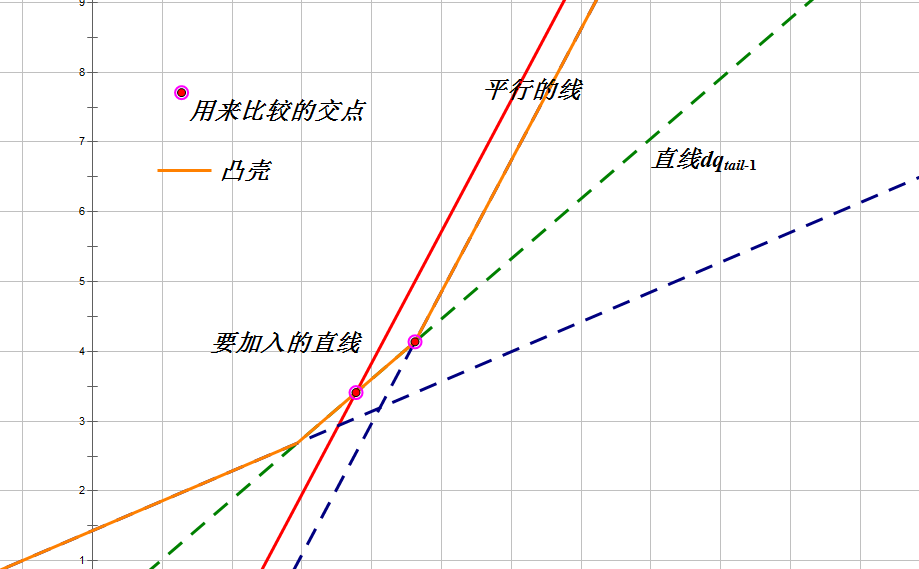
- 加入新直线时如果和直线平行,那么不加入当前直线;
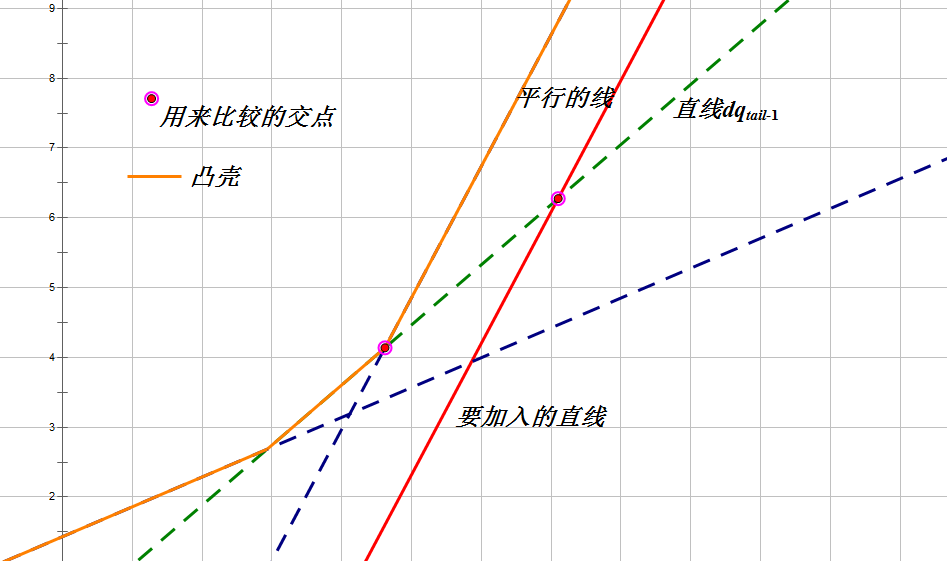
- 按照正常的操作弹出的直线,因为这时的判断仍然是对的;
- 原题要求输出方案,那每次记录一下分割点位置,倒着走一遍就好了,注释掉的语句就是记录方案的;
- 话说都是原题,洛谷为什么数据这么少,UOJ非hack数据都几十个...
代码:
#include <cstdio>const int MAXN=100005;//const int MAXK=205;int n,k;int sum[MAXN];//int pre[MAXK][MAXN];long long dp[2][MAXN];inline long long sqr(register long long x){return x*x;}inline int slope(int i){return sum[i];}inline long long y_itcpt(int i,int k){return dp[k&1][i]-sqr(sum[i]);}inline long long cal(int i,int j,int k){return (long long)slope(j)*sum[i]+y_itcpt(j,k);}inline double itsct(int i,int j,int k){return (double)(y_itcpt(j,k)-y_itcpt(i,k))/(slope(i)-slope(j));}inline long long slopeDP(){static int dq[MAXN];for(int i=1,head,tail;i<=k;++i){for(int j=1;j<=i;++j)dp[i&1][j]=0;head=tail=0,dq[0]=i;for(int j=i+1;j<=n;++j){while(head<tail && cal(j,dq[head],i-1)<=cal(j,dq[head+1],i-1))++head;//pre[i][j]=dq[head];dp[i&1][j]=cal(j,dq[head],i-1);while(head<tail && itsct(j,dq[tail-1],i-1)<=itsct(dq[tail],dq[tail-1],i-1))--tail;if(slope(j)!=slope(dq[tail])) dq[++tail]=j;}}return dp[k&1][n];}int main(){scanf("%d%d",&n,&k);for(int i=1;i<=n;++i){scanf("%d",&sum[i]);sum[i]+=sum[i-1];}printf("%lld",slopeDP());/*putchar('\n');for(int i=k,j=n;i;--i){j=pre[i][j];printf("%d ",j);}*/return 0;}
二分不单调决策
上面的练习都有一个共同的特点,就是自变量是单调的,这样我们每次可以将双端队列的开头直线不断弹出,让对于当前自变量的最优决策在队首。然而有一些题比较坑,自变量并不单调,这时我们不能再像之前那样弹队首了,只能通过二分来查找对于当前自变量的最优决策了。
1.[SDOI 2012] 任务安排
BZOJ上题面不完整。。。
任务按标号从~的顺序分批完成,不是任意顺序。
INT_MAXLLONG_MAX.
- 考虑到如果直接DP的话,会对后面造成影响(因为是按任务完成时刻计算的),不是无后效性的,我们需要将这个后效性通过一些方式消除;
- 不妨将每批任务对后面的影响转移到自身,那么DP方程就很好写了(为前缀和):
- 然而出题人硬是让时间可以倒流了,所以并不单调,我们不能弹了,
deque变成stack了,但是怎么快速找到自变量对应的最优决策是哪条直线呢?其实这是可以二分的,因为相邻的每两条直线的交点都是最优决策直线改变的界限:
- 二分的直线与上一条直线的交点在自变量右侧。这时,说明肯定不是当前最优决策直线。
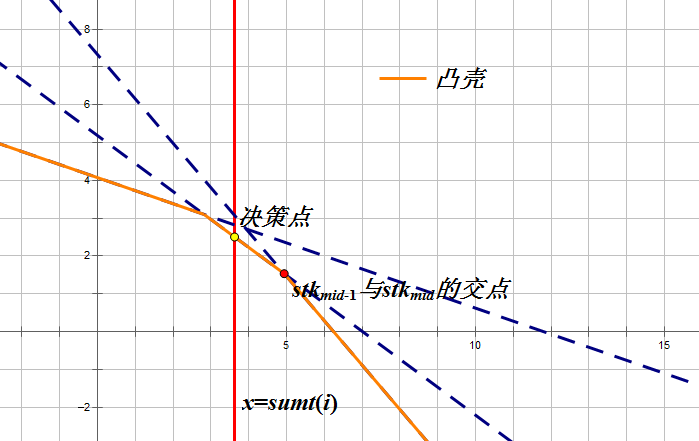
- 二分的直线与上一条直线的交点在自变量左侧。这时,说明肯定不是当前最优决策直线。
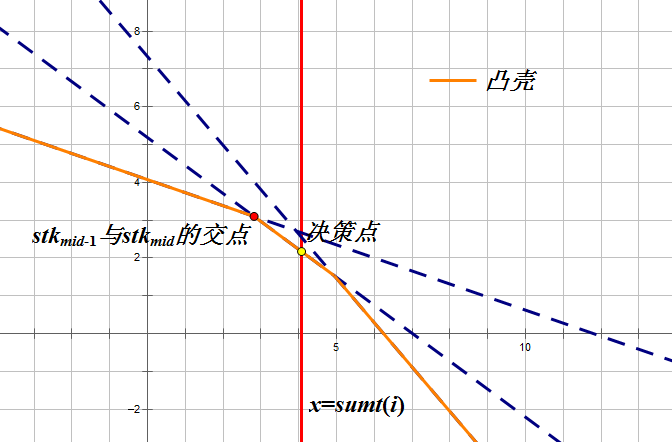
- 二分的直线与上一条直线的交点在自变量右侧。这时,说明肯定不是当前最优决策直线。
- 所以这题可以在的复杂度内解决了。
代码:
#include <cstdio>const int MAXN=300005;int n,s,top;int stk[MAXN];long long sumt[MAXN],sumf[MAXN],dp[MAXN];inline long long slope(int i){return -sumf[i];}inline long long y_itcpt(int i){return dp[i]-sumf[i]*s;}inline long long cal(int i,int j){return slope(j)*sumt[i]+y_itcpt(j);}inline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline int bin_chop(int now){int l=1,r=top,mid;while(l<=r){mid=l+r>>1;if(itsct(stk[mid],stk[mid-1])<=sumt[now])l=mid+1;else r=mid-1;}return stk[r];}inline long long slopeDP(){for(int i=1;i<=n;++i){dp[i]=cal(i,bin_chop(i))+sumt[i]*sumf[i]+sumf[n]*s;while(top && itsct(i,stk[top-1])<=itsct(stk[top],stk[top-1]))--top;if(slope(i)!=slope(stk[top])) stk[++top]=i;}return dp[n];}int main(){scanf("%d%d",&n,&s);for(int i=1;i<=n;++i){scanf("%lld%lld",&sumt[i],&sumf[i]);sumt[i]+=sumt[i-1],sumf[i]+=sumf[i-1];}printf("%lld",slopeDP());return 0;}
- 之前的题都是序列上的DP,这题居然整到了树上,但是观察发现,每个点的DP转移只与它到根的一条链有关,所以还按套路做就行了(为到根的距离):
- 而这里的自变量不是那种前缀和之类的,没有单调性,所以要像上一题一样二分找到最优决策;
- 但是还有一点,正常的插入直线操作是均摊复杂度的,也就是如果在树上这样做,插入的总复杂度是的,可能会被卡到,因此不能这样插入了;
- 观察到,插入直线依然是有单调性的(每次只能删除最后的一段连续的直线),我们还二分就好了,这样总复杂度就是稳定的了。(注意,其实只要记录栈里被覆盖的那个点回溯时恢复就可以了,弹出去的不用全记录,不修改就可以了)
代码:
#include <cstdio>const int MAXN=100005;int n;int v[MAXN],w[MAXN];int he[MAXN],dis[MAXN];int stk[MAXN];long long dp[MAXN];struct line{int to,nex,w;}ed[MAXN<<1];inline void addE(int u,int v,int w){static int cnt;ed[++cnt]=(line){v,he[u],w};he[u]=cnt;}inline int slope(int i){return -dis[i];}inline long long y_itcpt(int i){return dp[i];}inline long long cal(int i,int j){return (long long)slope(j)*v[i]+dp[j];}inline double itsct(int i,int j){return (double)(y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline int bin_chop_ln(int now,int r){int l=1,mid;while(l<=r){mid=l+r>>1;if(itsct(stk[mid-1],stk[mid])<=v[now])l=mid+1;else r=mid-1;}return stk[r];}inline long long slopeDP(int i,int top){return cal(i,bin_chop_ln(i,top))+w[i]+(long long)v[i]*dis[i];}inline int bin_chop_top(int now,int r){int l=1,mid;while(l<=r){mid=l+r>>1;if(itsct(now,stk[mid-1])>itsct(stk[mid],stk[mid-1]))l=mid+1;else r=mid-1;}return r;}void treeDP(int u,int fa,int top){dp[u]=slopeDP(u,top);top=bin_chop_top(u,top);int back_cur=++top,pre=stk[top];stk[top]=u;for(int i=he[u],v;i;i=ed[i].nex){v=ed[i].to;if(v!=fa){dis[v]=dis[u]+ed[i].w;treeDP(v,u,top);}}stk[back_cur]=pre;}int main(){scanf("%d",&n);for(int i=1,u,v,w;i<n;++i){scanf("%d%d%d",&u,&v,&w);addE(u,v,w),addE(v,u,w);}for(int i=2;i<=n;++i)scanf("%d%d",&w[i],&v[i]);for(int i=he[1],v;i;i=ed[i].nex){v=ed[i].to;dis[v]=ed[i].w;treeDP(v,1,0);}for(int i=2;i<=n;++i){printf("%lld",dp[i]);if(i!=n) putchar(' '); //卡输出}return 0;}
CDQ分治维护凸壳
上一个部分的题虽然自变量不单调了,但是直线斜率还是单调的,依然可以用双端队列或者栈维护。但是有些丧病的出题人把斜率也给搞的不单调了,这时只能用一些方法维护一个可以迅速从中间插入的凸壳了,传统方法是平衡树,但是那样代码量很大,常数也不小,而考虑到这里是可以离线维护的,我们可以用CDQ分治来解决(陈丹琪的论文就是用这个引入的Orz)。
- 这题信息量很大,要仔细读题...而且如果没有题目下面的提示,真的很难想。。。
- 考虑到如果某一天卖出会赚钱,肯定是都卖了优。因为我们是DP(贪心有后效性,肯定不可做),所以可以枚举是哪一天卖的,所以如果卖出赚钱,肯定都卖了赚的多,留一部分不卖赚不了钱,这个策略是正确的。而买入同理;
- 那么我们设是到了第天最多可以赚多少钱,和是到了第天最多可以有多少券;
- 那么我们可以得到朴素的DP方程(枚举哪一天卖完或者买入完):
- 其中第一个式子最外面的可以去掉,因为只要每次求完再用更新一下就好了;
- 那么我们考虑怎么快速求;
- 乍一看和之前斜率优化的形式不太相同,因为有两个形式的部分,既然这样,我们想办法变形消去一个:
- 由于对于每个,是固定的,所以最大化也就是最大化;
- 但是可以很明显发现,和都不单调,于是我们考虑通过排序消除一维影响,再通过分治消除另一维,额这就是CDQ分治嘛:
- 将原序列按照自变量排序进行分治,这样可以避免在凸壳上二分寻找决策点;
- 每次将分治的部分按照时间划分成两部分,先递归解决左区间,保证解的合法性;
- 之后将构造左区间直线的凸壳,由于划分时没有改变自变量的顺序,所以可以直接像普通斜率优化那样DP更新(因为每层分治都会更新一下)右区间的值,只是不把有区间的直线加入凸壳;
- 继续递归更新右区间的解;
- 最后考虑到左右区间都已经求出最终解,为了方便之后都右边的区间求解,将左右区间按照斜率归并排序;
- 由于左区间每次都已经按照斜率归并排序过了,所以其实第3条的构造凸壳就是直接按照普通斜率优化的方法插入就可以了,不用再单独排序了;
- 注意递归边界时,用第天的DP值来更新当前DP值,因为完整的DP方程还有一个求前缀最大值的部分;
- 考虑到每层分治其实就是扫三遍(划分、DP、归并排序),复杂度是的,所以总复杂度是,但是常数和代码量不知道比平衡树小到哪里去了。。。
代码:
#include <cstdio>#include <algorithm>#include <cstring>using std::sort;using std::max;const int MAXN=100005;int n;double a[MAXN],b[MAXN],rate[MAXN],ans[MAXN];struct dp_arr{int id;double a,b,x;double *ans;static bool cmp_x(const dp_arr &a,const dp_arr &b){return a.x<b.x;}}dp[MAXN];inline double slope(int i){return dp[i].a;}inline double y_itcpt(int i){return dp[i].b;}inline double cal(int i,int j){return slope(j)*dp[i].x+y_itcpt(j);}inline double itsct(int i,int j){return (y_itcpt(j)-y_itcpt(i))/(slope(i)-slope(j));}inline void separate(int l,int r){static dp_arr tmp[MAXN];int mid=l+r>>1;for(int cur=l,lp=l,rp=mid+1;cur<=r;++cur){if(dp[cur].id<=mid) tmp[lp++]=dp[cur];else tmp[rp++]=dp[cur];}memcpy(dp+l,tmp+l,(r-l+1)*sizeof(dp_arr));}inline void slopeDP(int l,int r){static int dq[MAXN];int mid=l+r>>1;int head=0,tail=0;for(int i=l;i<=mid;++i){while(head<tail && itsct(i,dq[tail-1])<=itsct(dq[tail],dq[tail-1]))--tail;if(slope(i)!=slope(dq[tail])) dq[++tail]=i;}for(int i=mid+1;i<=r;++i){while(head<tail && cal(i,dq[head])<=cal(i,dq[head+1]))++head;*dp[i].ans=max(*dp[i].ans,b[dp[i].id]*cal(i,dq[head]));}}void CDQ_DC(int l,int r){static dp_arr tmp[MAXN];if(l==r){//其实l=dp[l].id,但是现在dp[l-1].id可能不等于l了//所以这样写*dp[l].ans=max(*dp[l].ans,ans[dp[l].id-1]);dp[l].b=*dp[l].ans/(a[l]*rate[l]+b[l]);dp[l].a=dp[l].b*rate[l];return;}separate(l,r);int mid=l+r>>1;CDQ_DC(l,mid);slopeDP(l,r);CDQ_DC(mid+1,r);for(int cur=l,lp=l,rp=mid+1;cur<=r;++cur){if(rp>r || (lp<=mid && dp[lp].a<=dp[rp].a))tmp[cur]=dp[lp++];else tmp[cur]=dp[rp++];}memcpy(dp+l,tmp+l,(r-l+1)*sizeof(dp_arr));}int main(){scanf("%d%lf",&n,&ans[0]);dp[0].ans=&ans[0];for(int i=1;i<=n;++i){scanf("%lf%lf%lf",&a[i],&b[i],&rate[i]);dp[i].x=a[i]/b[i];dp[i].id=i,dp[i].ans=&ans[i];}sort(dp+1,dp+n+1,dp_arr::cmp_x);CDQ_DC(1,n);printf("%.3lf",ans[n]);return 0;}
