[关闭]
@zzy0471 2020-10-16T10:09:41.000000Z 字数 11513 阅读 673

常见排序算法的备忘记录和简单评测

算法

冒泡排序

  1. def sort(array:[int]):
  2.     """ 冒泡排序 """
  3.     length = len(array)
  5.     for i in range(length - 2, -1, -1):
  6.         for j in range(0, i + 1):
  7.             if array[j] > array[j + 1]:
  8.                 array[j], array[j + 1] = array[j + 1], array[j]

冒泡排序能入选本文，完全是因为情怀，相信很多人学习的第一个排序算法就是冒泡排序，当年第一次看到运行结果时，虎躯也是为之一震的。上面的代码，在我电脑上排序1万个数字用时7.5秒。

选择排序

  1. def sort(array:[int]):
  2.     length = len(array)
  3.     for i in range(length):
  4.         min_index = i
  5.         for j in range(i + 1, length):
  6.             if array[j] < array[min_index]:
  7.                 min_index = j
  8.         array[i], array[min_index] =  array[min_index], array[i]

这个算法的原理是：先找出最小的数，放在第一位，然后从第二位开始，在剩余数中找最小的数放第二位，依次类推。这种算法的交换次数很少，如果比较N个数，只需交换N次，比较次数为次。复杂度是平方级别的。此算法的优点就是简单，缺点是比较次数太多。且上一次的排序结果并不会对下一次排序有任何帮助。执行10000个随机数的排序，在我电脑上用了大约2.65秒，执行50000个随机数的排序的话，就非常慢了，在我电脑上等了67秒，如果数据量不大，用此算法比较简单方便，代码易读。

插入排序

  1. def sort(array:[int]):
  2.     length = len(array)
  3.     for i in range(1, length):
  4.         for j in range(i, 0, -1):
  5.             if array[j] < array[j - 1]:
  6.                 array[j], array[j - 1] =  array[j - 1], array[j]
  7.             else:
  8.                 break
  10. def sort2(array:[int]):
  11.     length = len(array)
  12.     for i in range(1, length):
  13.         for j in range(0, i):
  14.             if array[i] < array[j]:
  15.                 value = array[i]
  16.                 del(array[i])
  17.                 array.insert(j, value)
  18.                 break

这种算法的原理是：模仿打扑克抓牌，用第二个和第一个比较，如果第二个小，则插入到第一个前面，然后抓第三个，把低三个插入到前两张牌中适当的间隙中......。平均情况下，需要次比较和插入，复杂度也是平方级别。对于随机数来说，也不比选择排序好太多（其实更慢，但是我写了一个改进版，就是sort2，比选择排序快），在我机器上测试的结果是：排1万数据用了5.3秒，排5万数据用了130多秒。

我测试时候用的是随机数，如果待排序的数据本身是部分有序的，那么这种算法就比选择排序快了，选择排序对于待排序数据是否有序不敏感。

上面的代码我用了两种实现方法，第一种是通常的做法，第二种是利用了Python提供的对列表的一些便利性操作方法，我试着排序了1万数据用1.32秒，5万个数用了36秒。

希尔排序

  1. def sort(array:[int]):
  2.     length = len(array)
  3.     h = 1
  4.     while h < length // 3:
  5.         h = h * 3 + 1
  6.     while h >= 1:
  7.         for i in range(h, length):
  8.             for j in range(i, h - 1, -h):
  9.                 if array[j] < array[j - h]:
  10.                     array[j], array[j - h] =  array[j - h], array[j]
  11.                 else:
  12.                     break
  13.         h = h // 3

看名字就知道这个排序不简单，这是个以发明人的姓名命名的算法。上面介绍的选择排序、插入排序及冒泡排序，原理都比较简单，属于一般人经过苦思冥想也能想出来的算法，而希尔排序就精妙多了，非凡夫俗子所能为，它是对插入排序改进后的一种算法。

插入排序对于个数很少的数据或者是大致有序的数据非常有效，反之的话性能就下降了，希尔排序发扬了插入排序的优点，规避了插入排序的缺点，它的原理是这样：设置一个步长，使用插入排序，先把所有相隔为的元素给排序了，然后再选择一个小一点的步长，再使用插入排序，把所有相隔为的元素给排序了，如此下去，直到步长等于1为止。

刚开始排序时，虽然数据可能是无序的，但是架不住步长大，这样需要排序的元素并不多，插入排序很适合，当后面步长越来越小，虽然要排序的元素越来越多，但是架不住数据已经越来越大致有序了，这也是插入排序擅长的，希尔大佬真是聪明。

希尔排序的步长选择是关键，一般是选择这样的步长，选择比要排序数据长度的三分之一小的最大数，选择，后面每次选择的步长都是上一次的。为什么这样选最有效，我也不知道，反正我们听大佬的就行了，希尔算法的性能研究至今仍然是数学上的一个挑战。

我在我电脑上测试的结果是惊人的，排1万数据用了0.064秒，排5万数字用了0.5秒，了排50万个数字，用了1.21秒，排100万数据用了18.49秒。用插入排序排5万可用了130多秒呢，差距巨大。

如果数据量不是非常巨大，建议大家首选希尔排序，其代码简单，不需要开辟额外的空间，而且性能优越。

归并排序

  1. class Merage(object):
  2.     """ 归并排序 """
  3.     def __init__(self, l:[int]):
  4.         self.__temp = [0 for _ in range(0, len(l))] 
  5.         self.__list = l
  7.     def sort(self):
  8.         """ 归并排序 """
  9.         self.__sort_sub_array(self.__list, 0, len(self.__list) - 1)
  11.     def __sort_sub_array(self, array, lo, hi):
  12.         """ 排序一部分 """
  13.         if hi <= lo:
  14.             return
  15.         mid = lo + (hi - lo) // 2
  16.         self.__sort_sub_array(array, lo, mid)
  17.         self.__sort_sub_array(array, mid + 1, hi)
  18.         self.__merge(array, lo, mid, hi)
  20.     def __merge(self, array, lo, mid, hi):
  21.         """ 排序一部分
  23.         Args:
  24.             array: 待排序的数组
  25.             lo: 开始位置
  26.             hi: 结束位置
  27.             mid: 中间位置
  28.         """
  29.         for i in range(lo, hi + 1):
  30.             self.__temp[i] = array[i]
  32.         i = lo
  33.         j = mid + 1
  35.         for k in range(lo, hi + 1):
  36.             if i > mid:
  37.                 array[k] = self.__temp[j]
  38.                 j += 1
  39.             elif j > hi:
  40.                 array[k] = self.__temp[i]
  41.                 i += 1
  42.             else:
  43.                 if self.__temp[i] < self.__temp[j]:
  44.                     array[k] = self.__temp[i]
  45.                     i += 1
  46.                 else:
  47.                     array[k] = self.__temp[j]
  48.                     j += 1

归并排序是著名大神、现代计算机之父、博弈论之父、数学家、计算机科学家、物理学家冯·诺依曼发明的。这个算法代码就有点复杂了。归并排序的思想是：把一个数组分成两部分，分别排序后再归并为一个数组，归并后需保证全元素有序。归并的时候需要一个临时变量来暂时重放数据，总之就是分而治之，复杂度是对数级别的（实际上是），这就比之前的选择排序和插入排序平方级别的复杂度性能高很多，尤其是数据量大的时候，只是需要额外的空间周转一下。

归并排序的代码中，__merge方法是关键，此方法中，把数组中前半部分和后半部分，按照从小到大的规则归并回数组中去，需要一个中间变量暂时存储需要归并的元素。具体如下：

设两个“指针”i和j分别指向lo和hi位置的元素

我在我电脑测试的结果如下：1万数据排序需要0.0446秒，5万数据排序需要0.25秒，50万数据需要3.16秒，100万需要6.8秒。比希尔排序还厉害呢，数据太多时，归并排序比希尔排序更好，只是需要额外的空间，数据量不太大时，比如十几万，用希尔排序也不错，过了100万，归并排序优势明显（至少我的电脑是这样）。

快速排序

  1. def sort(array:[int]):
  2.     """ 快速排序 """
  3.     __sort_sub_aray(array, 0, len(array) - 1) 
  5. def __sort_sub_aray(array:[int], lo:int, hi:int):
  6.     """ 排序子数组 """
  7.     if lo >= hi:
  8.         return
  9.     j = __part(array, lo, hi)
  10.     __sort_sub_aray(array, lo, j - 1)
  11.     __sort_sub_aray(array, j + 1, hi)
  13. def __part(array:[int], lo:int, hi:int):
  14.     """  切分数组
  16.     用lo位置的元素切分数组，把lo位置元素放到适合的位置，使得它之前的所有元素不大于它，它之后的所有元素不小于它
  18.     Args：
  19.         array: 待切分数组
  20.         lo: 起点
  21.         hi: 结束点
  23.     Returns:
  24.         切分位置
  25.     """
  26.     v = array[lo]
  27.     i = lo + 1
  28.     j = hi
  30.     while True:
  31.         while i < hi and array[i] <= v:
  32.             i += 1
  33.         while array[j] > v:
  34.             j -= 1
  35.         if i >= j:
  36.             break
  37.         else:
  38.             array[i], array[j] = array[j], array[i]     
  39.     array[lo], array[j] = array[j], array[lo]  
  41.     return j

快速排序被誉为“二十世纪十大算法之一”，这可能是最常用的排序算法了。其发明人是英国计算机科学家霍尔。传说，霍尔因工作需求要做一个排序算法，刚开始想到的是冒泡排序，发现太慢，于是发明了快速排序，牛人就是牛，不经意间就做成了大事。

快速排序和归并排序类似，也用了分而治之的思想，复杂度是对数级别的，而且不用额外的空间，元素交换次数很少。其总体思想是：选择一个元素(通常选择第一个元素)，插入到合适的位置，并多通过左右大小数互换位置，把数组切分为两部分，使得该元素前面的都不大于自己，后面的都不小于自己，然后对前面的子数组和后面的子数组递归做同样的操作即可，其精华在于切分部分，非常巧妙，见方法__part。

该算法的缺点就是编码容易出错，我这个代码就调式了很久才好。不过现在网上论坛博客很多，应该可以很容易找到规范的代码，就是需要小心一点，做好测试工作。

我的测试结果是：排1万数字用时0.0197秒，排5万用时0.1142秒，排50万用时1.5秒，排100万用时3.2秒。比归并还要快啊，对得起“快速排序”这个名字。

优先队列

  1. import random
  2. import time
  4. class MaxPQ(object):
  5.     ''' 优先队列 '''
  7.     def __init__(self):
  8.         self.__array = [0]
  9.         self.__length = 0
  11.     def insert(self, v: int):
  12.         '''插入一个数.
  14.         Args:
  15.             v: 待插入的数
  16.         '''
  17.         self.__array.append(v)
  18.         self.__length += 1
  19.         self.__swim(self.__length)
  21.     def del_max(self) -> int:
  22.         '''返回最大值并从堆中删除.
  24.         Returns:
  25.             最大值
  27.         Raises:
  28.             ValueError: 堆中没有节点时抛出
  29.         '''
  30.         if self.__length < 1:
  31.             raise ValueError("堆中没有节点")
  33.         max = self.__array[1]
  34.         if self.__length > 1:
  35.             self.__array[1] = self.__array.pop()
  36.         self.__length -= 1
  37.         self.__sink(1)
  39.         return max
  41.     def __swim(self, k: int):
  42.         '''上浮一个节点.
  44.         Args:
  45.             k:节点索引
  46.         '''
  47.         while k > 1 and self.__less(k//2, k):
  48.             self.__exch(k//2, k)
  49.             k = k//2
  51.     def __sink(self, k: int):
  52.         '''下沉一个节点. 
  54.         Args:
  55.             k:节点索引
  56.         '''
  57.         while 2*k <= self.__length:
  58.             j = 2*k
  59.             if j < self.__length and self.__less(j, j + 1):
  60.                 j += 1
  61.             if not self.__less(k, j):
  62.                 break
  63.             self.__exch(k, j)
  64.             k = j
  66.     def __less(self, k1: int, k2: int) -> bool:
  67.         '''比较节点大小
  69.         Args: 
  70.             k1:第一个节点索引
  71.             k2:第二个节点索引
  73.         Return:
  74.             布尔值，表示k1节点是否小于k2节点
  75.         '''
  76.         return self.__array[k1] < self.__array[k2]
  78.     def __exch(self, k1: int, k2: int):
  79.         '''交换两个节点的值
  81.         Args:
  82.             k1:第一个节点索引
  83.             k2:第二个节点索引            
  84.         '''
  85.         self.__array[k1], self.__array[k2] = self.__array[k2], self.__array[k1]
  87.     def print(self):
  88.         if self.__length == 0:
  89.             print("empty")
  90.         else:
  91.             for i in range(1, self.__length + 1):
  92.                 print(self.__array[i], ' ')        
  94. if __name__ == "__main__":
  95.     pq = MaxPQ()
  97.     numbers = [random.randint(0, 10000) for _ in range(10001)]
  99.     start = time.perf_counter()
  101.     for n in numbers:
  102.         pq.insert(n)
  103.     top10 = []
  104.     for i in range(10):
  105.         top10.append(pq.del_max())
  107.     elapsed = time.perf_counter() - start
  108.     print("take:", elapsed, "s")
  110.     print(top10)

这个代码就有点长了，看官淡定。这个排序算法的应用场景和上面介绍过的有些不同，听我慢慢道来：不知各位放假回家是否用过飞猪预约火车票，这里有个选项，你可以选择多花20元、40元等来提高你的排队优先级，花钱越多，优先级就越高。从经济学角度考虑，这种模式是很好的，这样能在一定程度上保证对火车票需求愿望非常强烈的人得到票的概率大于愿望不是那么强烈的人，相当于以前的票贩子。当然，很少有一个方法能做到对所有人完全公平，肯定存在很多对火车票都有着强烈愿望的人，但是有些人经济条件好一些，有些差一些，前者有更大的概率获得车票，有钱，真的可以（在一定程度内）为所欲为。任何一个管理人的方案或政策都是权衡利弊的结果，比如疫情期间的口罩，国家就统一管控了，没有放任市场自身调节价格，如果没有管控，价格肯定会涨，有钱人会囤积更多的口罩，没钱的人可能一个都买不起，这样是符合市场规律了，但是站在一个更高点看这个问题，口罩分配不均，会让更多的人感染，造成非常大的社会危机。

扯远了，再回到飞猪，假设12306放出10张票，如何能快速找到优先级最高的10个人，这时就该优先队列上场了，优先队列是这样的一种队列，入队的每个元素带有优先级标志，不管你是第一个入队的，还是最后一个入队的，只要你的优先级最高，你就是第一个出队的。当有人预订车票时，把带有优先级标志的人放入优先队列，当有10张票放出来时，需从队列中找到优先级从高到低的前10个人来。这种算法的特点是不必为了排序前10个人而排序所有人然后取前10个。它至少提供两个接口：

上面的代码是用二叉堆实现的（一看到二叉两个字，就知道复杂度是对数级别的），所谓二叉堆，就是一颗堆有序的完全二叉树，由于是完全二叉树，所以可以非常巧妙的使用数组来存放，具体是这样的：把根节点存放在1的位置，0位置舍弃不用，根节点的两个子节点放在2和3位置，2的子节点放在4和5的位置，3的子节点放在6和7的位置，依次类推，你会发现，k位置的非根节点的父节点在k/2位置，两个子节点（如果存在的话）在2k和2k+1的位置上，这样，不用指针，完全用数组下标就可以方便找到某个节点的父节点和子节点。

现在先简单假设大的数表示优先级大，小的数表示优先级小，需保证二叉堆里每个节点都不小于它的两个子节点。入队时，把新元素追加到数组的最后，然后和它的父节点比较，如果比父节点大，则和父节点交换位置，交换后还比新的父节点大，则继续交换，直到交换到一个不比它小的父节点下面，这个过程叫上浮，请参加方法__swim；当要出队一个节点时，只需取根节点即可，它是最大的，取完后从堆里删除，然后把最后一个节点放到根节点填补空白，用新的根节点和它的两个子节点比较，取左子节点和右子节点中较大的节点，和根节点交换，交换后，如果它还是至少小于其中一个子节点，则再次交换，直到它的子节点都不大于它为止，这个过程叫下沉，参加方法__sink。这一顿操作过后，就实现了从n个数里取m个最大的数功能，还保证了二叉堆的结构没有被破坏，真是佩服这些数学家的大脑，他们发明的算法，功在当时，利在千秋。

我测试的结果：从1万个里排出最大的10个用时0.012秒，从10万个数里排出最大的10个用时0.12秒，从50万个数里排出最大的10个用时0.6秒，从100万个数里排出最大的10个用时1.21秒。

改进

实际上，就上面的需求，上述代码也许不是最佳做法，试想，夸张一点，有1000万人预约，就要搞一个节点数是1000万的堆吗？其实不用的，只要有一包含10个节点的堆就够了，我们现在来改进一下代码：构造这样一个堆，根节点最小，父节点小于等于子节点，和上面的代码相反。先把前10个数插入了，再来新数的话，先判断是否小于根节点，小于的话直接舍弃，因为根节点已经是10个里面最小的了，如果大于，则把根节点删除了（因为它是最小的），把新节点插入。这样就可以节省大量内存了且减少比较次数了。说干就干：

  1. import random
  2. import time
  4. class MinPQ(object):
  5.     ''' 优先队列 '''
  7.     def __init__(self):
  8.         self.__array = [0]
  9.         self.__length = 0
  11.     def get_length(self):
  12.         """ 长度 """
  13.         return self.__length
  15.     def insert(self, v: int):
  16.         '''插入一个数.
  18.         Args:
  19.             v: 待插入的数
  20.         '''
  21.         self.__array.append(v)
  22.         self.__length += 1
  23.         self.__swim(self.__length)
  25.     def del_min(self) -> int:
  26.         '''返回最小值并从堆中删除.
  28.         Returns:
  29.             最小值
  31.         Raises:
  32.             ValueError: 堆中没有节点时抛出
  33.         '''
  34.         if self.__length < 1:
  35.             raise ValueError("堆中没有节点")
  37.         min = self.__array[1]
  38.         if self.__length > 1:
  39.             self.__array[1] = self.__array.pop()
  40.         self.__length -= 1
  41.         self.__sink(1)
  43.         return min
  45.     def get_min(self) -> int:
  46.         '''返回最小值.
  48.         Returns:
  49.             最小值
  51.         Raises:
  52.             ValueError: 堆中没有节点时抛出
  53.         '''
  54.         if self.__length < 1:
  55.             raise ValueError("堆中没有节点")
  57.         min = self.__array[1]
  59.         return min
  61.     def __swim(self, k: int):
  62.         '''上浮一个节点.
  64.         Args:
  65.             k:节点索引
  66.         '''
  67.         while k > 1 and self.__more(k//2, k):
  68.             self.__exch(k//2, k)
  69.             k = k//2
  71.     def __sink(self, k: int):
  72.         '''下沉一个节点. 
  74.         Args:
  75.             k:节点索引
  76.         '''
  77.         while 2*k <= self.__length:
  78.             j = 2*k
  79.             if j < self.__length and self.__more(j, j + 1):
  80.                 j += 1
  81.             if not self.__more(k, j):
  82.                 break
  83.             self.__exch(k, j)
  84.             k = j
  86.     def __more(self, k1: int, k2: int) -> bool:
  87.         '''比较节点大小
  89.         Args: 
  90.             k1:第一个节点索引
  91.             k2:第二个节点索引
  93.         Return:
  94.             布尔值，表示k1节点是否大于k2节点
  95.         '''
  96.         return self.__array[k1] > self.__array[k2]
  98.     def __exch(self, k1: int, k2: int):
  99.         '''交换两个节点的值
  101.         Args:
  102.             k1:第一个节点索引
  103.             k2:第二个节点索引            
  104.         '''
  105.         self.__array[k1], self.__array[k2] = self.__array[k2], self.__array[k1]
  107.     def print(self):
  108.         if self.__length == 0:
  109.             print("empty")
  110.         else:
  111.             for i in range(1, self.__length + 1):
  112.                 print(self.__array[i], ' ')        
  114. if __name__ == "__main__":
  115.     pq = MinPQ()
  117.     numbers = [random.randint(0, 1000000) for _ in range(1000001)]
  118.     top10 = []
  120.     start = time.perf_counter()
  122.     for n in numbers:
  123.         if pq.get_length() < 10:
  124.             pq.insert(n)
  125.         else:
  126.             if n <= pq.get_min():
  127.                 continue
  128.             else:
  129.                 pq.del_min()
  130.                 pq.insert(n)
  132.     for i in range(10):
  133.         top10.append(pq.del_min())
  134.     top10.reverse()
  136.     elapsed = time.perf_counter() - start
  138.     print("take:", elapsed, "s")

如果用快速排序法解这问题，需要把数据都载入到内存，整个排了序，然后找出前10个，用优先队列的话，只需要10个长度的队列就可以了，速度飞快，我测试结果如下：从1万个里排出最大的10个用时0.0032秒，从10万个数里排出最大的10个用时0.029秒，从50万个数里排出最大的10个用时0.15秒，从100万个数里排出最大的10个用时0.31秒，起飞了！

堆排序

  1. class Heap(object):
  2.     ''' 堆排序 '''
  4.     def __init__(self, array:[int]):
  5.         self.__array = array
  6.         self.__length = len(array) - 1
  8.     def sort(self):
  9.         """ 堆排序 """
  10.         for i in range(self.__length//2, 0, -1):
  11.             self.__sink(i, self.__length)
  13.         n = self.__length
  14.         while n > 1:
  15.             self.__exch(1, n)
  16.             n -= 1
  17.             self.__sink(1, n)
  19.     def __sink(self, k:int, n:int):
  20.         '''下沉一个节点. 
  22.         Args:
  23.             k:节点索引
  24.             n:最后一个节点的位置
  25.         '''
  26.         while 2*k <= n:
  27.             j = 2*k
  28.             if j < n and self.__less(j, j + 1):
  29.                 j += 1
  30.             if not self.__less(k, j):
  31.                 break
  32.             self.__exch(k, j)
  33.             k = j
  35.     def __less(self, k1: int, k2: int) -> bool:
  36.         '''比较节点大小
  38.         Args: 
  39.             k1:第一个节点索引
  40.             k2:第二个节点索引
  42.         Return:
  43.             布尔值，表示k1节点是否小于k2节点
  44.         '''
  45.         return self.__array[k1] < self.__array[k2]
  47.     def __exch(self, k1: int, k2: int):
  48.         '''交换两个节点的值
  50.         Args:
  51.             k1:第一个节点索引
  52.             k2:第二个节点索引            
  53.         '''
  54.         self.__array[k1], self.__array[k2] = self.__array[k2], self.__array[k1]

堆排序的发明人是计算机科学家罗伯特·弗洛伊德。如果已经理解上了上面的优先队列，堆排序就很好理解了。它的思想是这样的：给定一个长度为n+1的数组array，把它看作一个堆，先把它堆有序化，这样一来，最大的元素就是在1位置的元素，然后把1位置的元素n位置的元素交换，交换后再对子数组array[1, n-1]进行堆有序化，然后再把1位置的元素和n-1位置的元素交换，交换后在堆子数组array[1, n-2]堆有序话.....如此来来回回，直到子数组只剩一个元素为止。具体如下：

假设原始堆是这样的：

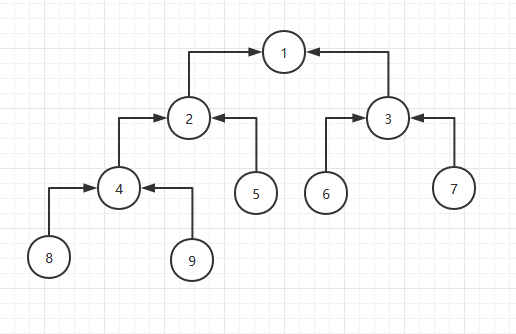
image.png-14.8kB

其中数字代表节点在数组中的位置，不是节点的值。

第一步是把array[1,9] 堆有序化，只需要将4，3，2，1分别做下沉操作即可，对应代码：

  1. for i in range(self.__length//2, 0, -1):
  2.     self.__sink(i, self.__length)

从总数的一半开始往前遍历下沉节点即可，后一半都是叶子节点，无需下沉了。这步执行完毕后如下图：

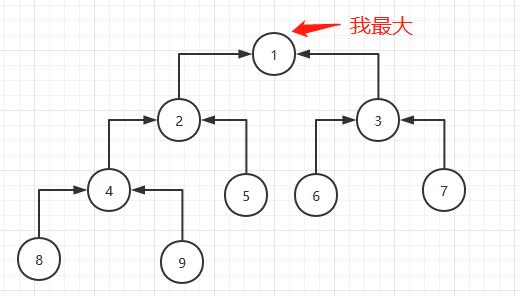
image.png-14.9kB

第二步是把堆顶节点和最后一个节点交换，对应代码：

  1. self.__exch(1, n)

这个时候最大的数在数组最后：

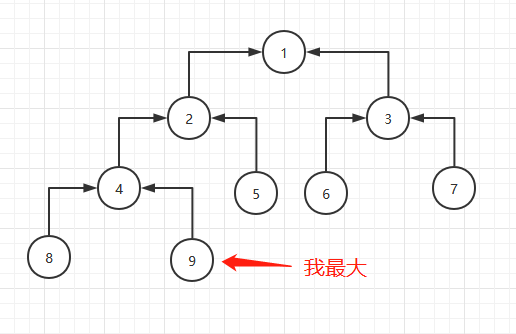
image.png-15.9kB

第三步是把array[1,8]再堆有序化:

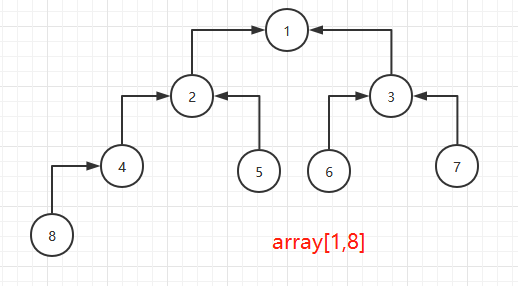
image.png-14.1kB

由于堆顶的两个子堆已经有序，仅需下沉堆顶即可，对应代码：

  1. self.__sink(1, n)

下沉完毕后堆顶就是次大的数：

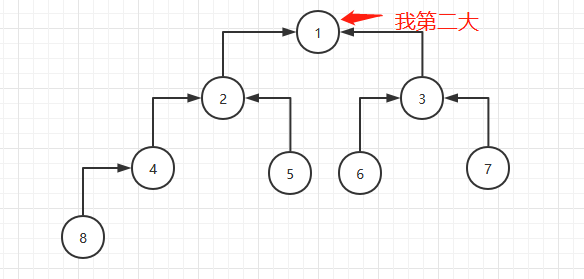
image.png-15kB

然后在循环体里把堆顶和数组中倒数第二个元素交换：

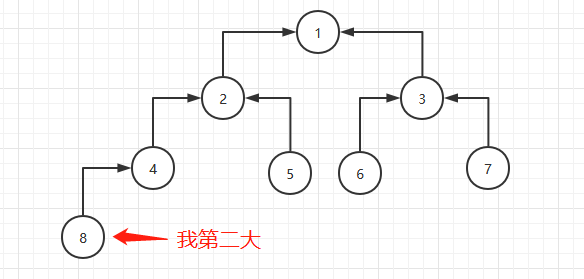
image.png-15kB

重复第二步、第三步，直到子数组里只有一个元素为止，这时，数组就是从小到大排列了（不包括数组的第一个元素，因为代码里没用到，是从索引位置1开始的)

又到了快乐的测试时间。排1万个用时0.083秒，排10万个用时1.12秒，排50万个用时6.52秒，排100万个用时14.47秒

计数排序

理论上，基于比较和交换的排序算法最小的复杂度就是O(NLogN)了，但是，在某些特定条件下，速度还可以提升，不用比较和交换的方法，比如计数排序，复杂度为O(N+K)，其中N是排序数的数量，K是排序数的范围值，在下例中，K等于100：

  1. import time
  2. import random
  4. def sort(array:[int], max: int):
  5.     """ 计数排序 """
  6.     container = [0 for _ in range(max + 1)]
  7.     for n in array:
  8.         container[n] += 1
  10.     i = 0
  11.     for j in range(0, max + 1):
  12.         for _ in range(container[j]):
  13.             array[i] = j
  14.             i +=1  
  16. if __name__ == "__main__":
  18.     numbers = [random.randint(0, 100) for _ in range(10001)]
  20.     start = time.perf_counter()
  21.     sort(numbers, 100)
  22.     elapsed = time.perf_counter() - start
  24.     print("take:", elapsed, "s")

这个算法是HaroldH.Seward发明的，并没有找到关于这位大神的详细信息。当所排数都为整数，且范围不是太大时，这个排序算法简直飞起来：首先创建一个临时数组container，长度为K，元素默认值为0，然后遍历待排序数组，当遍历到数n时，将container[n]加1，这趟循环结束后，再遍历一遍container，如果container[k]为m，则打印m个k，当一切结束时，你会发现打印出来的数字已经有序。

我的测试结果：排序1万数字用时0.001秒，排序5万数字用时0.006秒，排序10万数字用时0.01秒，排序50万数字排序0.06秒，排序100万数字用时0.12秒，逆天了。

不过清注意条件：

添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注