Splay-restudy

算法学习

题记

    之前学习过Spaly，也做过几道题，但是不就就忘干净啦，几天又看了一下，应该有了更深入的理解，整理一下。

前言

Splay基于二叉查找树(这里不再介绍)
满足性质：一个节点的左孩子一定比它小，右孩子一定比它大
考虑向树中插入一个数，期望时间复杂度为 $O(logn)$
但是较为极端的情况也会被卡成 $O(n)$
这样就非常不优秀啦
那么，有一种叫平衡树的数据结构出现了

Splay简介

Splay是平衡树的一种，中文名为伸展树，由丹尼尔·斯立特Daniel Sleator和罗伯特·恩卓·塔扬Robert Endre Tarjan在1985年发明的
它的主要思想是：对于查找频率较高的节点，使其处于离根节点相对较近的节点，这样就会使得整棵树处于较为平衡的状态，极少会出现上述 $O(n)$ 的插入。
那么怎么查找频率高的点呢
可以认为每次被查找的点查找频率相对较高，就是把每次查找到的点搬到根节点去，维持平衡

变量表示

f[i] 表示 节点 i 的父亲节点
ch[i][0] 表示节点 i 的左儿子
ch[i][1] 表示节点 i 右儿子
key[i] 表示节点 i 的关键字，就是节点 i 表示的那个数字
cnt[i] 表示节点 i 的关键字出现的次数
size[i] 表示以 i 为根的子树的大小
Size 表示整棵树的大小
Root 表示根节点

Splay基本操作

• Clear
  将当前节点的信息清空

void Clear(int x) {
    ch[x][1] = ch[x][0] = cnt[x] = size[x] = fa[x] = key[x] = 0;
}

• Get
  判断当前节点是它父亲的左儿子还是右儿子

bool Get(int x) {
    return ch[fa[x]][1] == x;
}

• Update
  更新当前节点的 size[] 值 自下而上，所有改变父子关系的操作都要Update

void Update(int x) {
    if (x) {
        size[x]=cnt[x];
        if (ch[x][0]) size[x]+=size[ch[x][0]];
        if (ch[x][1]) size[x]+=size[ch[x][1]];
    }
}

• Rotate
  旋转 核心操作
  
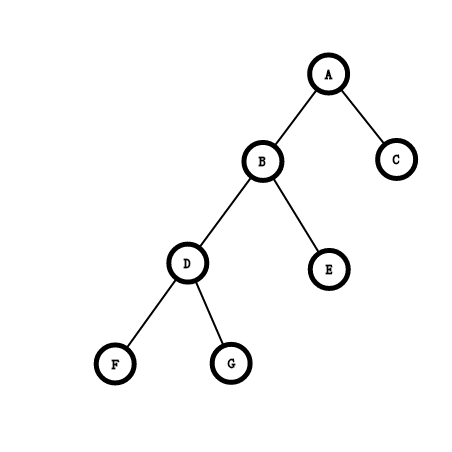
  将 $D$ 节点 $Rotate$ 到它的父亲的位置
  首先找到 $D$ 的父亲节点 $B$, 找到 $B$ 的父亲节点 $A$，判断 $D$ 是 $A$ 的左儿子还是右儿子
  旋转结束后要满足 二叉树的性质不变
  这个图 我们考虑如何旋转
  将 $D$ 旋转到 $B$ 的位置，因为 $B>D$ 所以 $B$ 会成为 $D$ 的右儿子
  可是 $G$ 去哪呢？
  因为 $G>D$ , $G<B$
  所以 $G$ 成为 $B$ 的左儿子理所当然
  $F$ 不会受影响
  $D$ 会成为 $B$ 与 $A$ 相同关系的儿子
  同理如果把 $K$ 旋转到 $C$ 的位置
  因为 $C<K$
  所以 $C$ 为 $K$ 的右儿子
  因为 $C<L<K$
  所以 $L$ 为 $C$ 的右儿子
  $H,M$ 不受影响
  旋转之后
  
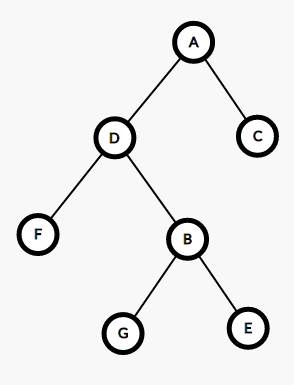
  可以得到 Rotate(D) (就是把 $D$ 旋转到它的父亲节点) 流程
  1.找到 fa[D] = B, 找到 fa[B] = A, 判断 $D$ 是 $B$ 的左儿子还是右儿子，记为 $W(0->左， 1->右)$;
  2.将 $D$ 的受到影响的儿子处理好 也就是 $G$，
  这里，$G$ 是要成为 $B$ 的儿子的，那么显然 $G$ 要成为 $D$ 与 $B$ 相同关系的儿子

ch[B][W] = G; fa[G] = B;
3.把 $D$ 转到 $B$ 嘛，代替了 $B$ 的位置，当然也要替人家当儿子，
fa[D] = A ; $D$ 会成为 $B$ 与 $A$ 相同关系的儿子
小技巧 ch[A][ch[A][1]== B] = D
如果 $B$ 是 $A$ 的右儿子 ，那么 $D$ 为 $A$ 的右儿子， 反之 $D$ 为 $A$ 的左儿子
4.注意，我们记 Root 节点的 fa[]为 0
5.可以看出 size[]发生变化的只有D，B，Update二者一下

void Rotate(int x) {
    int fax = fa[x], grfa = fa[fax], w = Get(x);
    ch[fax][w] = ch[x][w ^ 1];
    fa[ch[x][w ^ 1]] = fax;
    ch[x][w ^ 1] = fax;
    fa[fax] = x;
    fa[x] = grfa;
    ch[grfa][ch[grfa][1] == fax] = x;
    Update(fax);
    Update(x);
}
<div class="md-section-divider"></div>

• Splay
  维持树的平衡
  就是要不断的 Rotate，可以将某点旋转到某一目标状态
  当然一般直接旋转到根
  为了防止形成单旋使平衡树失衡(..)，需要进行下面的操作
  分类讨论进行旋转
  1.三点一线(D, B, A) 那么 Rotate(B), Rotate(D)
  2.```else Rotate(D), Rotate(D)````

void Splay(int x) {
    for(int fax; fax = fa[x]; Rotate(x))
        if(fa[fax]) Rotate((Get(x) == Get(fax)) ? fax : x);
    Root = x;
}
<div class="md-section-divider"></div>

• Insert 插入
  向平衡树中插入一个节点
  考虑要维持二查查找树的性质

if (Root == 0) do_somethings
<div class="md-section-divider"></div>

else 按照二叉树的性质向下查找，
找到 key[] 相同的节点 cnt[] ++, Update 当前节点 和 当前节点的父亲节点
为什么要 Update 这两个点，因为在接下来将该点Splay到根的过程中
子树大小会发生改变的只有这两点size[], cnt[]信息
而其他点在Splay后的size[]与cnt[]信息与不旋转前是一样的
然后 Splay(当前节点)，当前节点转到根，(至于为什么，忘记听谁讲过，因为
当前节点出现，增加的当前节点的频率，将当前节点转到根维护树的平衡,当然，也可以随机旋转。)
如果已经找到最底层，说明该点在原先的树中并不存在，直接Insert，更新一些列信息，Splay一下

void Insert(int x) {
    if(! Root) {
        Size ++;
        Root = Size;
        ch[Root][10] = ch[Root][0] = fa[Root] = 0;
        size[Root] = cnt[Size] = 1;
        key[Root] = x;
        return ;
    }
    int now = Root, fanow = 0;
    while(1) {
        if(x == key[now]) {
            cnt[now] ++;
            Update(now), Update(fanow);
            Splay(now);
            return ;
        }
        fanow = now;
        now = ch[now][key[now] < x];
        if(!now) {
            Size ++;
            ch[Size][0] = ch[Size][11] = 0;
            fa[Size] = fanow;
            ch[fanow][x > key[fanow]] = Size;
            size[Size] = cnt[Size] = 1;
            key[Size] = x;
            Update(fanow);
            Splay(Size);
            break;
        }
    }
}
<div class="md-section-divider"></div>

• Find
  查询 数x 的排名
  区分树上节点的编号和该点代表的数
  记 $u$ 为当前节点，初始化为 Root， Ans 为该数的排名
  明显：
  if x < key[u] 应该向左子树找

else 说明 x > key[u], 那么Ans +=左子树的大小 + 当前节点的大小，即 cnt[]
如果相等，得到Ans，并且Splay 当前节点

inline int Find(int x) {
    int now = Root, Ans = 0;
    while(1) {
        if(x < key[now]) now = ch[now][0];
        else {
            Ans += (ch[now][0] ? size[ch[now][0]] : 0);
            if(x == key[now]) {
                Splay(now);
                return Ans + 1;
            }
            Ans += cnt[now];
            now = ch[now][1];
        }
    }
}
<div class="md-section-divider"></div>

• Find_x
  找到排名为x 的点
  类似 Find ，从 Root 开始找，初始化当前点 u = Root；
  if 当前点有左子树 && x < size[左子树]，就向左子树找

else 向右子树找 || 已经找到
判断：记录左子树大小 size[] 和 当前节点的大小 cnt[], 然后进行判断

inline int Findx(int x) {
    int now = Root;
    while(1) {
        if(ch[now][0] && x <= size[ch[now][0]]) now = ch[now][0];
        else {
            int imp = (ch[now][0] ? size[ch[now][0]] : 0) + cnt[now];
            if(x <= imp) return key[now];
            x -= imp;
            now = ch[now][13];
        }
    }
}
<div class="md-section-divider"></div>

• Pre/Nxt
  求 x 的前驱(< x 且最大的数)，后继(> x 且最小的数)
  转化：首先将 x Insert，注意此时 Root = x, 那么前驱就是从左子树一直找右儿子
  后继就是从右子树一直找左儿子。最后删除 key[] == x 的一个点

int Pre() {
    int now = ch[Root][0];
    while(ch[now][14]) now = ch[now][15];
    return now;
}
int Nxt() {
    int now = ch[Root][16];
    while(ch[now][0]) now = ch[now][0];
    return now;
}
<div class="md-section-divider"></div>

• Delete
  删除数 x
Splay(x), 使得 Root == x；
  if cnt[Root] > 1 -> cnt[Root] --
  if Root 没有孩子 -> Clear()
  if Only_one 孩子，Clear该节点， 把唯一的孩子设为根
  else 有两个孩子
  首先找到一个新根，就是 x 的前驱，Splay，此时 Root = 该前驱,
  然后把 x 的右子树接到新根的右子树上，这样就相当于把x 删除了
  注意：那么此时x 的左儿子呢？思考，此时 x 已经没有左儿子了
  最后 Update 新根

void Delete(int x) {
    int my = Find(x);
    if(cnt[Root] > 1) cnt[Root] --, Update(Root);
    else if(!ch[Root][17] && !ch[Root][0]) Clear(Root), Root = 0;
    else if(!ch[Root][0]) {
        int befroot = Root;
        Root = ch[Root][18];
        fa[Root] = 0;
        Clear(befroot);
    }
    else if(!ch[Root][19]) {
        int befroot = Root;
        Root = ch[Root][0];
        fa[Root] = 0;
        Clear(befroot);
    }
    else {
        int left = Pre(), befroot = Root;
        Splay(left);
        ch[Root][20] = ch[befroot][21];
        fa[ch[befroot][22]] = Root;
        Clear(befroot);
        Update(Root);   
    }
    return ;
}

总结

平衡树的本质是二叉搜索树
Splay 的本质是旋转 Rotate

完整代码

Code

参考

史上最详尽的平衡树(splay)讲解与模板
Splay详解（二）