@mayiyang
2021-05-01T03:20:40.000000Z
字数 4786
阅读 1041
一类树上相关问题选讲(锟题选讲)
##
documents
简介
树上路径相关问题在近期算法竞赛中多次出现,该类题主要涉及求解树上某些路径或点对的信息最值或求和之类,在思路与实现上更偏重于代码实现,通常代码结构比较复杂繁琐,融入多种树上基础算法。锟题可以被广义的理解为较为综合的数据结构题目。
以下会结合若干实例分析。
若无特殊说明,我们总认为树的大小和询问次数的大小为级别
解决树上问题若干重要算法
重链剖分
定义 重子节点 表示其子节点中子树最大的子结点。如果有多个子树最大的子结点,取其一。如果没有子节点,就无重子节点。
定义 轻子节点 表示剩余的所有子结点。
从这个结点到重子节点的边为 重边。
到其他轻子节点的边为 轻边。
若干条首尾衔接的重边构成 重链。
可以发现,当我们向下经过一条 轻边 时,所在子树的大小至少会除以二。
树上的每条路径都可以被拆分成不超过 条重链。
通过把树上路径用重链拆分,使用数据结构维护重链上信息,在进行合并计算,是解决树上路径问题的好方式
树上启发式合并
重儿子定义与上一小节类似。
遍历节点时,采用如下策略:
先遍历 的轻儿子,并计算答案,但 不保留遍历后它对全局数组的影响;
遍历它的重儿子,直接继承重儿子信息,保留它对全局数组的影响。
根节点到树上任意节点的轻边数不超过 条,又因为如果一个节点是其父亲的重儿子,则他的子树必定在他的兄弟之中最多,所以任意节点到根的路径上所有重边连接的父节点在计算答案是必定不会遍历到这个节点,所以一个节点的被遍历的次数等于他到根节点路径上的轻边树 ,所以一个节点的被遍历次数 。
你平心静气,拍案而起, 这样做时间复杂度为,不失为离线处理的优秀方案。
线段树合并
字面意思,将权值线段树直接合并。
若我们要不断去除某个叶子,并将该叶子的所有信息不改变的合并至父亲,并获取在某一个范围内的元素的信息或本次合并过程的信息,就可以考虑使用线段树合并的方式实现。(这一特点常用于优化特殊的二维树上动态规划)
如果按照退栈顺序进行合并,线段树合并还能起到固定的作用。这意味着,当我们依次把某个节点的所有子树信息合并到这个节点上时,每次合并时两个集合之间的点对的最近公共祖先都是这个节点,而线段树合并时还可以得出合并的两个集合中的点对的某些信息,这使得在某些情况下,我们可以把树上路径拆成两个端点、来考虑。
若合并信息的复杂度为 ,且保证每次均有至少一点被合并,线段树合并的总时间复杂度一般仅为,而且应用灵活、容易实现,是非常实用的一种工具。
虚树
树上有若干关键点,若仅仅关心两点距离等不需完全依赖原树的信息,可以考虑把这个点以及所有提取出来。
乍一看点数很多,但你可以拿起笔,在草稿纸上涂涂画画,突然发现每次至少会把两点缩成,该点集对应虚树大小不超过点集大小的两倍!
借助这点,虚树有如下应用:
1.直接处理一类树上关键点问题
2.有两棵树,对第一棵树做树分治,每次得到的点集对应到第二棵树上建虚树。
3.有一棵树及 条给定的路径,枚举路径最近公共祖先,并对同一最近公共祖先的
所有路径端点建虚树。
树分治
如果我们要计算的信息是可合并的,那么我们可以通
过点分治或边分治将链信息拆分成两个从某个分治中心出发的前缀链信息。
这么做往往只是在单次处理的时间复杂度的基础上乘上 ,所以对于
很多问题,我们都可以先考虑通过树分治尝试将问题简化,得出 的算法之后再考虑优化。
额外点一下点分治,即在分治中心处将子树按照大小排序,不断选择子树直至大小超过,可以证明每次最劣划分为,复杂度与三度化边分相同。之后若无特殊情况,例题时不对点分边分区别。
Examples
CTSC2018暴力写挂
description
给定两棵个点、边带权的树,定义,求最大的
solution1
式子中好几次,如果能枚举一个就好。
带着这个目的转化,先对第一棵树分治,到分治中心距离为
原式
在第二棵树上建虚树,记分治中心两边点为黑点、白点,一遍,计算子树内黑白点权值最大值,合并即可。
虚树按照 dfs 序排序部分的复杂度瓶颈可以在分治处理子问题结束之后由子问题的结果向上使用归并的方式快速得到。很快啊,我们就一只了!
solution2
上述方法不错,但是代码中枯燥的分类无聊透顶,令人心生倦怠
f[x] = g[x][0] = g[x][1] = -inf;if (Col[x] == 0) checkmax(g[x][0], Value[x]);if (Col[x] == 1) checkmax(g[x][1], Value[x]);for (int i = first[x]; ~i; i = nxt[i]){int to = point[i];dp(to);if (g[x][0] > -inf && g[to][1] > -inf) checkmax(f[x], g[x][0] + g[to][1]);if (g[x][1] > -inf && g[to][0] > -inf) checkmax(f[x], g[x][1] + g[to][0]);if (g[to][0] > -inf) checkmax(g[x][0], g[to][0]);if (g[to][1] > -inf) checkmax(g[x][1], g[to][1]);}
而且上一框中最后几句话挺重要的,"使用归并的方式快速得到"?
注意到,边分树也是一个深度为 的二叉树,和线段树非常相似。线段树都有线段树合并,凭什么边分树没有合并?如果把边分树看做线段树,我们也可以在上面进行类似的合并操作---我们对第一棵树建立边分树,并记录每个分治中心到对应范围内每个点的距离。
由于单次合并前第二棵树上的最近公共祖先已经确定,我们只需要在边分树结构里记录每一个边分中心每一侧节点的
的最大值,在合并的时候更新答案即可。
这样也是单log,但舒服好多!
WC2018通道
description
给定三棵有非负边权的树,定义一棵树上两点距离为两点间最短路径边权和。问一对
点在三棵树上的距离和的最大值为多少。
solution1
考虑在第一棵树上树分治,在第二棵树上建出虚树之后再次树
分治。然后在第三棵树上再建虚树、再次树分治。
每个点获得了一个权值,代表它到三个分治中心的距离之和,而且我们知道每个
点在三棵树上边分治时在哪一侧。
我们枚举其中一个点分别位于三次分治的哪一侧,另一个点得分别位于三次分治的另
一侧,最优解即两边可能的点的权值最大值的和。
不断树分治,思路简单,容易地得到了一个时间复杂度为 的
算法,但实际运行甚至不如暴力
solution2
第三次分治好浪费啊!!!
假设点 在前两棵树中与分治中心的距离之和为 ,那么在第三棵树上,对
于每个点 x,我们新建一个点 x′ ,并在 x 与 x' 之间连一条权值为 的边。
问题被转化成求所有在前两棵树中均处于分治中心两侧的点对在第三棵树上
的最远距离。
由于边权非负,两点集并的直径端点必为点集内直径的四个端点,信息已合并,所以我们可以轻松解决。
因此,时间复杂度仅剩两个(nice)。
solution2_ex
可以不对第二棵树进行树分治吗?真行!
在对第一棵树的分治过程中,我们将点集内的点分成了两种,这两种点分别位于分治
中心两侧。
设 表示节点 x 在第 棵树中的深度,设 表示点对 (x, y) 在第 棵树上的
距离,设 表示节点 x 在第一棵树中与当前分治中心的距离。
设点对 在第二棵树上的最近公共祖先为,则 与 在三棵树中的距离之和可以稍加整理得到
如果固定了,剩下的问题仍然可以转化为最远点对问题。
注意到点集的最远点对是支持快速合并,也就是说我们只需要在第二棵树中进行一次深度优先遍历,并不断将子树的点集向上合并,维护点集在第三棵树上的最远点对,计算合并时产生的新的不同种类点之间的最远点对。
由于单次求点对距离的时间复杂度可以通过预处理降至 ,且虚树按照 dfs 序排序部分的复杂度瓶颈可以在边分治处理子问题结束之后由子问题的结果向上使用归并的方式快速得到。我们真的一只了!(虽然有一说一,我写的单log败给两log)
reflection
无脑树分治不会有的,先尝试通过树分治简化问题,然后要善于抓住题目性质,想方设法的优化。树分治仅仅是一把刀,关键看持刀人。
NOI2018情报中心
description
给定一棵 个节点的树,边有权。
给定 条路径,每条路径有一个权重。
对于所有至少有一条边相交的路径对,求它们路径并所有边权之和减去这两条路径各自的权值得到的结果的最大值。
或者判定没有合法的路径对。
边权和路径权值非负。
solution
“至少有一条边相交的路径对”,这总不太能树分治了。在草稿纸上涂涂画画,你会发现,两路径相同/不同,似乎不是很一致,下面分类考虑。
solver1(different lca)
此时两链相交部分为直上直下的链,附上下图
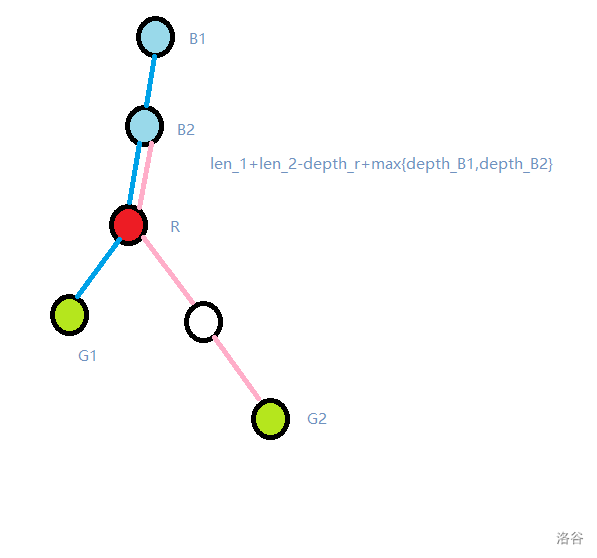
遍历每个,维护
线段树合并可以做,具体而言:
稍加合并即可
solver2(same lca)
直接枚举,然后对于这些链端点建出虚树,变成题中子任务
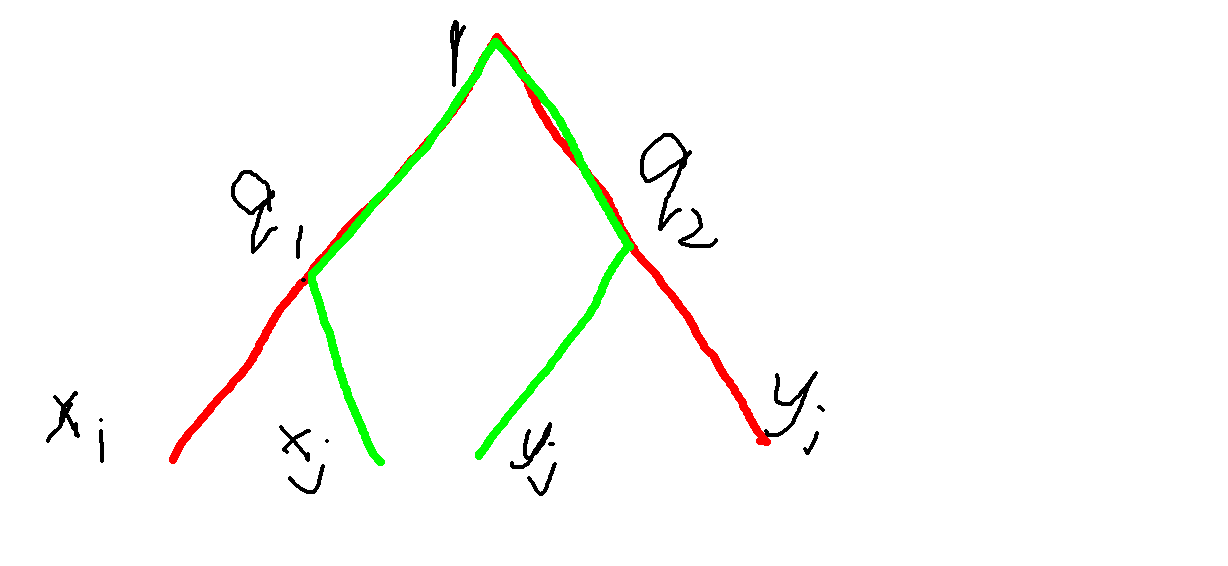
然后树形,固定,维护相关信息即可
总结
引用论文的话结尾:
通过上述例题,可以体会到树分治和虚树在简化树上问题时起到的巨大作用,而线段树合并往往解决了问题的最后一步。在处理这些问题时,我们往往可以先尝试使用树分治或者虚树简化问题,然后尝试将问题转化成线段树合并或者其他算法可以解决的问题。
总之这些树上算法运用灵活,效果显著,应用广泛,需要耐心体会。
参考文献
- 张哲宇. 浅谈树上分治算法. IOI2019 中国国家候选队论文集, 2019
- 周镇东. 浅谈一类树上路径相关问题. IOI2021 中国国家候选队论文集, 2021
- 董永建,宋新波,徐先友等,《信息学奥赛一本通 (C++版)》,科学技术文献出版社
