Report: Knight's Tour

Lintcode Recursion

题目

• link

  The knight is placed on the first block of an empty board and, moving according to the rules of chess, must visit each square exactly once.

  • Example: a board of 8x8, a knight(即'马')goes RI. Find a tour it can go over each square once and only once, so 63 steps to finish the board.

• 题型: Recursion, Backtracking

• 类型题: Word break, 8 queen, ...
• 参考: 回溯法1,2,3

怎么想?

• 和backtracking的所有问题一样, 通过recursion, 以及param中的result param来prune, 看for loop里面选择的下一步是否满足条件, 如果满足就继续找, 否则退出.
• recurrence function: helper(int[][] steps, int step, int row, int col), 这里的steps是result param, 其余为state param. 例如helper(steps, 1, 0, 0), 这是knightTour调用helper的起点. 即代表: 从(0,0)点开始找第一个step的有效方案. 这里的有效方案是指从这里出发能找到knight tour遍历所有点一次的方案.

First trial: WRONG!

• 先是搞混了: 到底是设置当前的坐标为step, 还是step+1? 还是说设置next坐标为step还是step+1???
  
  • 其实设置当前坐标或者next 坐标都可以. 不过都是设置为step. 可以参考GeekForGeek或者ACMerBlog.

• 但是具体怎么写呢? 我一开始在for loop里面只是call了一次helper(). 见helperWRONG. 这样就出现了forever loop. 为什么?

  • 写之前要想好algs.
  • 每一个step有2个结果:
    
    1. 无效: 即发现这一步的格子已经用过了. 直接backtrack, 即将这个格子设为-1.
    2. 有效: 什么叫有效的操作? 并不是isValid()==true!!! 而是走了这一步之后, 能找到一个方案使得遍历棋盘并且每一步都不重复.

• 于是因为我不是真正的理解回溯(即回溯无效操作), 所以我的没有结果, 一直运行. (

ACMer's solution

• ACMer: 关于回溯算法的详细介绍可以参考：回溯法（1）,回溯法（2）,回溯法（3）.
• set/reset的是current index.
• 在for循环8个方向中, 开始recursion call. 而对于recursion call不是call就行了的, 而是目的要明确, 通过递归调用, 找到从这个点出发的有效方案, 若没有则返回false, 于是要回溯, 即这个点重置. 若是能找到有效方案, 就直接true return了, 也就不用回溯了!
• 代码:

public boolean helperACMer(int[][] steps, int step, int row, int col) {
    steps[row][col] = step;
    if (step == size) {
      return true;
    }
    for (int i = 0; i < 8; ++i) {
      int next_x = row + dx[i];
      int next_y = col + dy[i];
      if (isValid(steps, next_x, next_y)) {
        if (helperACMer(steps, step + 1, next_x, next_y) == true) {
          return true;
        }
      }
    }
    steps[row][col] = -1;
    return false;
}

• 输出是:

[[1, 46, 35, 26, 3, 12, 17, 14]
[36, 49, 2, 45, 28, 15, 4, 11]
[47, 58, 27, 34, 25, 18, 13, 16]
[50, 37, 48, 59, 44, 29, 10, 5]
[57, 60, 51, 38, 33, 24, 19, 22]
[52, 39, 54, 43, 30, 21, 6, 9]
[61, 56, 41, 32, 63, 8, 23, 20]
[40, 53, 62, 55, 42, 31, 64, 7]]
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64]

GeekForGeek's solution

• 很好理解, 给出了思路, 以及如何使用回溯法解决这种要search的问题. Search一个有效方案即要遍历所有可能的方案, 找到有效的方案. 所以这种题是回溯问题.
• 写code前要先写好算法, 否则越写越糊涂!
• 代码:

public boolean helperGeek(int[][] steps, int step, int row, int col) {
    // save temp result
    if (step == size) {
      return true;
    }
    // backtracking with prune
    Integer[] shu = new Integer[]{4, 5, 6, 7, 3, 2, 1, 0}; //{0,1,2,3,4,5,6,7};
    List<Integer> list = Arrays.asList(shu);
//    Collections.shuffle(list);  WHY the shuffle leads the helper gointo forever ???
    for (int s : list) { // recursion for all eight direction
      if (!isValid(steps, row + dx[s], col + dy[s])) {
        continue;
      }
      /**
       * I got confused: the next_x, next_y should have step number: step or step+1, or I should assign
       * current x,y with step or step+1?
       */
      steps[row + dx[s]][col + dy[s]] = step;
      /**
       * found a Knight traverse then return. NOTICE: this is recursion call, so ??? times recursion,
       * I got this recursion call result. Can be earlier if recursion failed.
       */
      if (helperGeek(steps, step + 1, row + dx[s], col + dy[s]) == true) {
        return true;  // !!!
      } else {
        steps[row + dx[s]][col + dy[s]] = -1;
      }
    }
    return false;  // !!!
}

• 思路: 和LCA, 01背包一样, 都是要清晰的设计好算法, 以及其中的Invariant, 并用英语说出的话, 基本上就没问题了. 否则写出来的代码越写月乱, 就连reverse linked list也会错!
  

  • If all squares are visited
    print the solution

  • Else
    a) Add one of the next moves to solution vector and recursively
    check if this move leads to a solution. (A Knight can make maximum
    eight moves. We choose one of the 8 moves in this step).
    b) If the move chosen in the above step doesn't lead to a solution
    then remove this move(回溯) from the solution vector and try other
    alternative moves.
    c) If none of the alternatives work then return false (Returning false
    will remove the previously added item in recursion and if false is
    returned by the initial call of recursion then "no solution exists" )

  • 输出:

  
  

[[0, 11, 24, 29, 52, 33, 50, 63]
[13, 22, 27, 32, 25, 30, 53, 34]
[10, 1, 12, 23, 28, 51, 62, 49]
[5, 14, 21, 26, 31, 60, 35, 54]
[2, 9, 4, 59, 44, 55, 48, 61]
[15, 6, 17, 20, 39, 36, 43, 56]
[18, 3, 8, 45, 58, 41, 38, 47]
[7, 16, 19, 40, 37, 46, 57, 42]]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]

思念起

• 为什么我的Java结果和ACMer或者GeekForGeek的不同, 而他们或者我的结果每次输出都一样?

  • 因为我的dx, dy不一样. 也即move的顺序不同, 所以结果不一样.
  • 8x8有there are 33,439,123,484,294!!!个解. 见OSU的reu paper.

• 怎样才能random iterate 8个方向?

  • 如果是简单的iterate很简单, 用collections.shuffle, 然后for loop就行.
  • 但是recursion里面怎样保证每次都random, 且每个数都遍历一遍?
  • 我在helper里面直接shuffle, 结果没有输出...
    
    • 已经可以了, 方法就是在param里面加入list.
  • 算法是什么?
    
    • 面试常考: Fisher-Yates
    • 还常考random iterator.
    • 如何test?

Helper Shuffle

• 我刚尝试了shuffle, 其实可以的, 关键是for之前shuffle就行了, 这样保证了advanced for loop可以遍历8个方向, randomly.
• 代码:

public boolean helperShuffle(int[][] steps, int step, int row, int col, List<Integer> list) {
    if (step == SIZE) {
      return true;
    }
    Collections.shuffle(list);
    for (int i : list) {
      int next_x = row + dx[i];
      int next_y = col + dy[i];
      if (isValid(steps, next_x, next_y)) {
        steps[next_x][next_y] = step;
        if (true == helperShuffle(steps, step+1, next_x, next_y, list)) {
          return true;
        }
        else {
          steps[next_x][next_y] = -1;
        }
      }
    }
    return false;
  }

• 输出: 我用的是3*10的棋盘, 因为8*8的棋盘+shuffle很慢, 我以为是我的shuffle写错了. 其实没有, 只是shuffle加上就很慢? 奇怪.

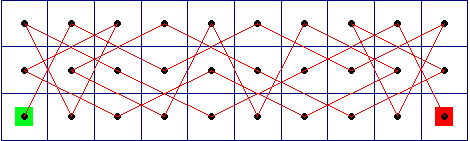
[[0, 9, 6, 13, 26, 3, 28, 19, 24, 21]
[7, 14, 11, 2, 5, 16, 25, 22, 29, 18]
[10, 1, 8, 15, 12, 27, 4, 17, 20, 23]]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]
[[0, 3, 12, 15, 26, 7, 10, 21, 28, 23]
[13, 16, 5, 2, 11, 18, 27, 24, 9, 20]
[4, 1, 14, 17, 6, 25, 8, 19, 22, 29]]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]