Hindley-Milner类型系统（3）

类型系统 Haskell

---

我们已经了解了HM类型系统的六条规则，但我们如何可以用它做什么？

答案是：类型推导和类型检查。

类型推导的职责是：在一个类型系统设定的环境里，给出任意一个符合语法的表达式，类型推导器可以自动推断出其唯一最为通用的类型，它被称做Principal Type。

如果一个表达式的Princple Type不存在，或者不可确定，则推导失败。而在类型推导的过程中，会伴随着类型检查。如果发现不符合类型系统规则的情况，也会导致失败。下面就是这个目标的形式化定义：

$$\begin{align*} \Gamma \vdash^{\scriptscriptstyle R} e : \sigma \end{align*}$$

在一个类型系统下，一个表达式可能具备的最为通用的类型被称为Principal Type。类型推演的目标就是找到任意表达式的Principal Type。

为了明白上述规则如何帮助我们完成这个目标，我们再来回顾一下这门简单语言的语法构造：

$$\begin{align*} e\ \ & = \ \ x \\ &\ \ |\ \ \ \ e_{1}\ e_{2} \\ &\ \ |\ \ \ \ \lambda x.e \\ &\ \ |\ \ \ \ \mathbf{let}\ x = e_{1}\ \mathbf{in}\ e_{2} \end{align*}$$

然后，我们对照那六条类型规则。会发现前四条规则：VAR, APP, ABS和LET，它们的conclusion部分和这门语言的语法构造是一一对应的。而从逻辑学的角度，如果一个逻辑的前提，是结论的充要条件，那么我们就把结论当作前提，把前提当作我们要推理的结论，反向构造整个推理过程。

但问题在于：另外两条规则：INST和GEN，在这套规则系统中，和语法没有任何直接的对应关系，也没有明确指出应该在什么地方，以什么样的方式，什么样的顺序使用。也就是说，它们尚不能被直接转化成算法。

为了能让规则直接体现为算法，就有必要制定出更加清晰的，让每条规则都有明确选择时机和选择顺序的类型规则。这样，我们只需要根据表达式的语法结构，就可以自然的选择类型规则。

而这样的规则被称作语法制导（syntax-directed）规则。

语法制导规则

按照$\sigma$的定义，我们会发现$\forall \alpha. \sigma$ 依然是一个 $\sigma$，因而，这意味着:

$$\begin{align*} & \forall \alpha. \tau \\ & \forall \alpha. \forall \alpha_{1}. \tau \\ & \forall \alpha. \forall \alpha_{1}. \ldots \forall \alpha_{n}.\tau \end{align*}$$

无论如何，所有的$\forall$都在前面。正如$\lambda x. \lambda y. z$可以写成$\lambda x\ y.z$一样，$\forall \alpha.\forall \alpha_{1}. \ldots \forall \alpha_{n}.\tau$也可以写成$\forall \alpha\ \alpha_{1} \ldots\alpha_{n}.\tau$。

如果我们用$\overline\alpha$代表其所有参数的集合，那么$\sigma$就可以被定义为：

$$\begin{align*} \sigma \ \ & = \ \ \tau \\ &\ \ |\ \ \ \ \forall \overline\alpha.\tau \end{align*}$$

现在我们定义如下算法：

$$\begin{align*} \mathbf{gen}(\Gamma, \tau)= \begin{cases} \forall \overline\alpha.\tau & \quad \mathbf{free}(\tau) - \mathbf{free}(\Gamma) = \overline\alpha \\ \tau & \quad \mathbf{free}(\tau) - \mathbf{free}(\Gamma) = \Phi \end{cases} \end{align*}$$

我们用如下形式来表示这个算法：

$$\begin{equation*} \Gamma \vdash^{gen} \sigma \succeq \tau \end{equation*}$$

另外，对于$\overline\alpha$，我们可以针对它的每一个参数，都用一个在现有环境中尚不存在的全新类型变量来替换，我们就实例化了一个更为具体的类型。比如：

$$\begin{align*} (\forall \alpha_{0}. \forall \alpha_{1}. \tau)\ \tau_{0}\ \tau_{1}\ \ \succeq \ \ [\alpha_{0} \mapsto \tau_{0},\alpha_{1} \mapsto \tau_{1}]\ \tau \end{align*}$$

现在我们定义如下算法：

$$\begin{align*} inst(\Gamma, \sigma)= \begin{cases} [\overline\alpha \mapsto \overline\tau]\ \tau & \quad \forall \overline\alpha . \tau \\ \tau & \quad \tau \end{cases} \end{align*}$$

我们用如下形式来表示这个过程：

$$\begin{equation} \Gamma \vdash^{inst} \sigma \succeq \tau \end{equation}$$

在HM类型系统里，产生这两条规则的原因只有一个，那就是let binding。因为只有在let binding里才能做到多态。

比如： $\textbf{let } f = \lambda x. x \textbf{ in } f\ f$里，$\lambda x.x$本身的类型是$\tau \rightarrow \tau$（参见ABS规则），而$f$的类型为$\forall \alpha. \alpha \rightarrow \alpha$（参见LET规则）。这个赋值的过程，就是运用$\Gamma \vdash^{gen}$算法的时机。

然后$f$被存储在本地环境里，以方便于$\mathbf{let \ldots in }\ f\ f$里使用$f$时，可以从环境中找到。

而从环境中查找一个变量，正是规则VAR提供的算法。对于我们这个例子，从环境中查找到$f$后，其类型是$\forall \alpha. \alpha \rightarrow \alpha$，而在具体的表达式$f\ f$里，这个类型必须被实例化。这里正是$\Gamma \vdash^{inst}$被应用的时机，也是HM类型系统里，唯一需要应用INST规则的时机。

而这也是HM的四条主规则里，只有LET和VAR里的类型用到了$\sigma$的原因。

然后我们重新定义VAR和LET规则，再加上原来的ABS和APP，就得到了如下四条类型规则:
$\newcommand{\typerule}[3]{\cfrac{#1}{#2}\scriptstyle{\mathrm{#3}}\displaystyle}$

$$\begin{align*} \typerule{x:\sigma \in \Gamma \ \ \ \ \Gamma \vdash^{inst} \sigma \succeq \tau}{\Gamma \vdash x:\tau}{VAR} \end{align*}$$
$$\begin{align*} \typerule{\Gamma \vdash e_{0}:\tau' \ \ \ \ \Gamma \vdash^{gen} \sigma \succeq \tau' \ \ \ \ \Gamma,x:\sigma \vdash e_{1}:\tau}{\Gamma \vdash \mathbf{let}\ x=e_{0}\ \mathbf{in}\ e_{1}:\tau}{LET} \end{align*}$$

$$\begin{align*} \typerule{\Gamma, x:\tau \vdash e:\tau'}{\Gamma \vdash \lambda x.e:\tau \rightarrow \tau '}{ABS} \end{align*}$$

$$\begin{align*} \typerule{\Gamma \vdash e_{0}:\tau \rightarrow \tau' \ \ \ \ \Gamma \vdash e_{1}:\tau}{\Gamma \vdash e_{0}\ e_{1}:\tau'}{APP} \end{align*}$$

这就是我们想要的语法制导规则。

基于约束的推演

我们得到了一组语法制导的规则。下面我们通过一个例子来看看如果利用这组规则来推导一个表达式的类型。

$$\begin{align*} \textbf{let}\textbf{ f = }\lambda x. x \textbf{ in }\textbf{f f} \end{align*}$$

我们根据类型规则，可以自底向上明确的重建出整个类型的证明树（proof tree）：

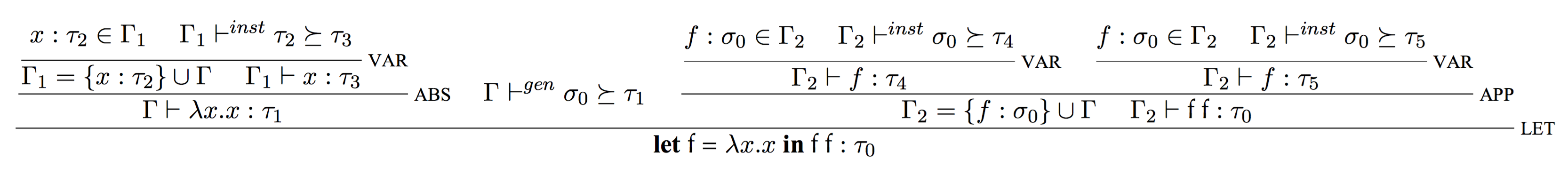
我们可以看到，在这颗证明树上有很多带有标号的$\tau$和$\sigma$，它们的存在是因为，在构建这颗证明树的过程中，碰到的每个term我们都还不知道其真正的类型。

所以，我们先给这些term一个类型标识，被称作元类型变量（Meta Type Variable）。然后我们再分析元类型变量之间的关系，最终推演出类型。

而这些元类型变量之间的关系，就是我们得到的一系列约束。伴随着证明树的重建，每次应用一个规则，就会自动产生一个约束。

对于上面这个例子，产生的约束及其过程，如下所示：

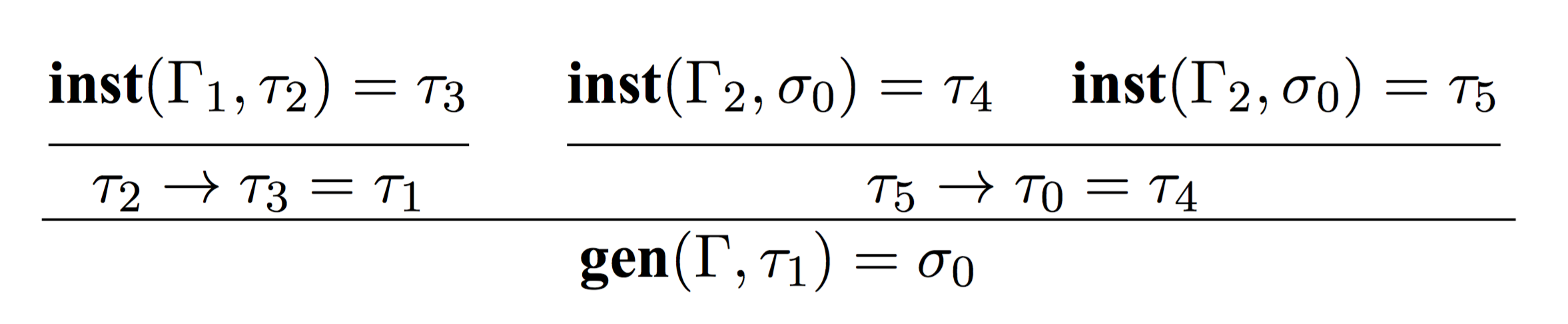
我们将所有的约束罗列在一起，然后来分析约束之间的关系。

$$\begin{align*} \tau_{2} \rightarrow \tau_{3} & = \tau_{1} \\ \tau_{5} \rightarrow \tau_{0} & = \tau_{4} \\ inst(\Gamma_{1}, \tau_{2}) & = \tau_{3} \\ gen(\Gamma, \tau_{1}) & = \sigma_{0} \\ inst(\Gamma_{2}, \sigma_{0}) & = \tau_{4} \\ inst(\Gamma_{2}, \sigma_{0}) & = \tau_{5} \end{align*}$$

首先需要明确：我们的目标是推出$\tau_{0}$。

• 先从 $\textbf{inst}(\Gamma_{1}, \tau_{2}) = \tau_{3}$ 开始，由于$\tau_{2}$不是一个polytype，因而$\tau_{2} = \tau_{3}$；
• 然后我们可以从 $\tau_{2} \rightarrow \tau_{3} = \tau_{1}$ 得出 $\tau_{2} \rightarrow \tau_{2} = \tau_{1}$；
• 再运用 $\textbf{gen}(\Gamma,\tau_{1}) = \sigma_{0}$，可以得到 $\sigma_{0} = \forall \alpha. \alpha \rightarrow \alpha$；
• 有了$\sigma_{0}$，我们就可以从$\textbf{inst}(\Gamma_{2}, \sigma_{0}) = \tau_{4}$推出$\tau_{6} \rightarrow \tau_{6} = \tau_{4}$；
• 同样的，从$\textbf{inst}(\Gamma_{2}, \sigma_{0}) = \tau_{4}$推出$\tau_{7} \rightarrow \tau_{7} = \tau_{5}$；
• 由于$\tau_{5} \rightarrow \tau_{0} = \tau_{4}$，所以可以推出$\tau_{6} \rightarrow \tau_{6} = \tau_{5} \rightarrow \tau_{0}$；因而：$\tau_0 = \tau_{5} = \tau_{6} = \tau_{7} \rightarrow \tau_{7}$。

至此，我们成功的推出了结果：$\tau_{0} = \tau_{7} \rightarrow \tau_{7}$。

表达式的推演结果是一个monotype，如果将其转化为polytype，则运用$\textbf{gen}(\Gamma, \tau_{0})$得到$\forall \alpha. \alpha \rightarrow \alpha$。但这一步骤，只有当之前的表达式，在一个更大的let表达式里对变量赋值时才会发生，比如：

$$\begin{align*} \textbf{let}\textbf{ g = } (\textbf{let}\textbf{ f = }\lambda x. x \textbf{ in }\textbf{f f}) \textbf{ in } \ldots \end{align*}$$

需要特别强调的是，正如我们之前提到的：inst算法，是通过产生全新的类型变量对polytype进行实例化：这就做到做到了一举两得的作用：

1. 避免了和环境中已有的自由变量冲突的可能性;
2. 同一个名字f，每次出现，都会产生一次新的实例化，由于实例化后得到的类型是一个monotype。因而f的两次实例化得到的类型是不同的。而这正是$f$实现多态化的关键。

表达式$\textbf{let }x = e' \textbf{ in }e$定义的变量$x$，先被泛化为$\sigma$（polytype）；随后，变量$x$在表达式$e$里的每次出现，其类型$\sigma$都会被实例化为不同的monotype，这就是let polymorphsim的全部秘密。

Unification

对于一组类型等式构成的集合，首先Unfication是一个对等号两侧的类型进行模式匹配和变量替换的过程。

对于mototype，简单的检查等式两侧是否属于相同即可，任何一个等式不成立，都导致Unfication的失败。下面是一组例子：

$$\begin{align*} \textbf{Int = Int} \ \ \ \ & \Rightarrow \ \ \ \ pass\\ \textbf{Int = Bool} \ \ \ \ & \Rightarrow \ \ \ \ fail \\ \textbf{Int} \rightarrow \textbf{Bool} = \textbf{Int} \rightarrow \textbf{Bool} \ \ \ \ & \Rightarrow \ \ \ \ pass \\ \textbf{Int} \rightarrow \textbf{Bool} = \textbf{Int} \rightarrow \textbf{Int} \ \ \ \ & \Rightarrow \ \ \ \ fail \end{align*}$$

对于带有变量的等式，通过模式匹配，对变量进行求值。比如下面的例子：

$$\begin{align*} \textbf{Int} \rightarrow \textbf{Bool} = \tau_{0} \ \ \ \ & \Rightarrow \ \ \ \ \tau_{0} \mapsto \textbf{Int} \rightarrow \textbf{Bool} \\ \textbf{Int} \rightarrow \textbf{Bool} = \textbf{Int} \rightarrow \tau_{0} \ \ \ \ & \Rightarrow \ \ \ \ \tau_{0} \mapsto \textbf{Bool} \\ \textbf{Int} \rightarrow \textbf{Bool} = \textbf{Bool} \rightarrow \tau_{0} \ \ \ \ & \Rightarrow \ \ \ \ fail \\ \tau_{0} \rightarrow \tau_{1} = \tau_{2} \rightarrow \tau_{3} \ \ \ \ & \Rightarrow \ \ \ \ \tau_{0} \mapsto \tau_{2},\ \tau_{1} \mapsto \tau_{3} \\ \tau_{0} \rightarrow \tau_{1} = \tau_{2} \ \ \ \ & \Rightarrow \ \ \ \ \tau_{2} \mapsto \tau_{0} \rightarrow \tau_{1} \\ \tau_{0} \rightarrow \tau_{1} \rightarrow \tau_{2} = \tau_{3} \rightarrow \tau_{4} \ \ \ \ & \Rightarrow \ \ \ \ \tau_{3} \mapsto \tau_{0},\ \tau_{4} \mapsto \tau_{1} \rightarrow \tau_{2} \\ (\tau_{0} \rightarrow \tau_{1}) \rightarrow \tau_{2} = \tau_{3} \rightarrow \tau_{4} \ \ \ \ & \Rightarrow \ \ \ \ \tau_{3} \mapsto \tau_{0} \rightarrow \tau_{1},\ \tau_{4} \mapsto \tau_{2} \end{align*}$$

一旦找到一个变量的求值，在整个集合内对这个变量进行替换，从而消除掉这个变量。除了我们的目标变量之外，其它的变量都可以消除。
$\newcommand{\letexpr}[4]{\textbf{let}\textbf{ #1 = } #2 \textbf{ in }\textbf{#3}:#4}$
现在回到我们之前的例子。对于一个$\letexpr{x}{e'}{e}{\tau}$这样的表达式，无论从其求值语义，还是LET规则，$x=e'$与$e$都有先后顺序。

在类型推演过程中，$x=e'$的目的是用来得出变量$x$的类型，然后通过gen将其泛化，然后用于$e$的类型推演中。

因而，我们先对$x=e'$侧产生的约束进行unify。

首先，由于unification所需的是等式，所以，我们需要先把inst规则转化为等式，从而得到如下约束集合及unify过程：

$$\begin{align*} \{\tau_{2} = \tau_{3},\tau_{2} \rightarrow \tau_{3} = \tau_{1}\} [\tau_{2} \mapsto \tau_{3}] \\ \Rightarrow \{\tau_{3} \rightarrow \tau_{3} = \tau_{1}\} \end{align*}$$

然后调用$\textbf{gen}(\Gamma,\tau_{1}) = \sigma_{0}$，可以得到$\sigma_{0} =\forall \alpha. \alpha \rightarrow \alpha$。然后在调用右侧产生的inst，然后开始下面的unify过程：

$$\begin{align*} \{\tau_{6} \rightarrow \tau_{6} = \tau_{4}, \tau_{7} \rightarrow \tau_{7} = \tau_{5},\tau_{5} \rightarrow \tau_{0} = \tau_{4} \} [\tau_{4}\mapsto\tau_{6}\rightarrow\tau_{6}] \\ \Rightarrow \{ \tau_{7} \rightarrow \tau_{7} = \tau_{5},\tau_{5} \rightarrow \tau_{0} = \tau_{6}\rightarrow\tau_{6} \} [\tau_{5}\mapsto\tau_{7}\rightarrow\tau_{7}] \\ \Rightarrow \{ (\tau_{7} \rightarrow \tau_{7})\rightarrow \tau_{0} = \tau_{6}\rightarrow\tau_{6} \} [\tau_{6}\mapsto\tau_{7}\rightarrow\tau_{7}] \\ \Rightarrow {\tau_{0} = \tau_{7} \rightarrow \tau_{7}} \end{align*}$$

最终，我们成功的推演出表达式的类型为：$\tau \rightarrow \tau$。

通过这个例子，我们可以总结出类型推演的原理：

类型推演，是根据表达式的语法结构，运用语法制导的类型规则，得到一组约束，然后对这组约束进行Unify，从而得到表达式类型的过程。

推演过程中的自由类型变量

$\newcommand{\letexpr}[4]{\textbf{let}\textbf{ #1 = } #2 \textbf{ in }\textbf{#3}:#4}$
现在我们看看表达式$\lambda y. \letexpr{f}{\lambda x.x\ y}{f}{\tau}$的类型推演过程。

首先，根据四条类型规则，我们得到了如下证明树：

最外层是一个$\lambda$表达式，但$\lambda$内部是一个$\mathsf{let}$表达式。从上一个例子我们知道$\mathsf{let}$表达式的类型推演分成了三个步骤。所以，我们首先推演出$f$的类型为：

$$\begin{align*} \tau_{3} = (\tau_{1} \rightarrow \tau_{5}) \rightarrow \tau_{5} \end{align*}$$

然后我们运用gen进行泛化。通过查看我们的证明树，可知，$\tau_{1}$属于环境$\Gamma_{1}$里的自由变量，因而:

$$\begin{align*} \sigma_{0} = \textbf{gen}(\Gamma_{1},\tau_{3}) = \forall \alpha. (\tau_{1} \rightarrow \alpha) \rightarrow \alpha \end{align*}$$

然后回到右侧，在VAR规则里，通过inst进行实例化：

$$\begin{align*} \tau_{8} = \textbf{inst}(\Gamma_{3}, \sigma_{0}) = (\tau_{1}\rightarrow\tau_{9})\rightarrow\tau_{9} \end{align*}$$

最后产生的全部约束为：

$$\begin{align*} \tau_{8} & = (\tau_{1}\rightarrow\tau_{9})\rightarrow\tau_{9} \\ \tau_{2} & = \tau_{8} \\ \tau_{0} & = \tau_{1}\rightarrow\tau_{2} \end{align*}$$

不难发现，之前泛化时的自由类型变量$\tau_{1}$，依然存在于现在的约束里。它之所以能成为$\sigma$的自由变量，是因为它是更外层（如果从证明树的角度看，更底层）表达式的类型变量。

外层表达式类型所包含的类型变量，会成为内层表达式类型的自由类型变量。

最后，将这些约束进行Unifiy，推演出来的类型为: $\tau_{1} \rightarrow(\tau_{1}\rightarrow\tau_{9})\rightarrow\tau_{9}$。

失败的推演

从$\lambda$演算理论里，如下等价关系成立：

$$\begin{align*} \textbf{let}\mathsf{\ f = }\lambda x. x \mathbf{\ in \ }\mathsf{f\ f}\ \ \ \ \equiv\ \ \ \ \textbf{let}\mathsf{\ f = }\lambda x. x \textbf{ in } (\lambda x. x\ x) \mathsf{\ f} \end{align*}$$

但在HM类型系统下，其类型推演过程会失败。而失败的原因在于表达式$\lambda x. x\ x$。我们先做按照HM类型规则进行一次推演，看看为何会失败。

首先，我们还是先建立其证明树：

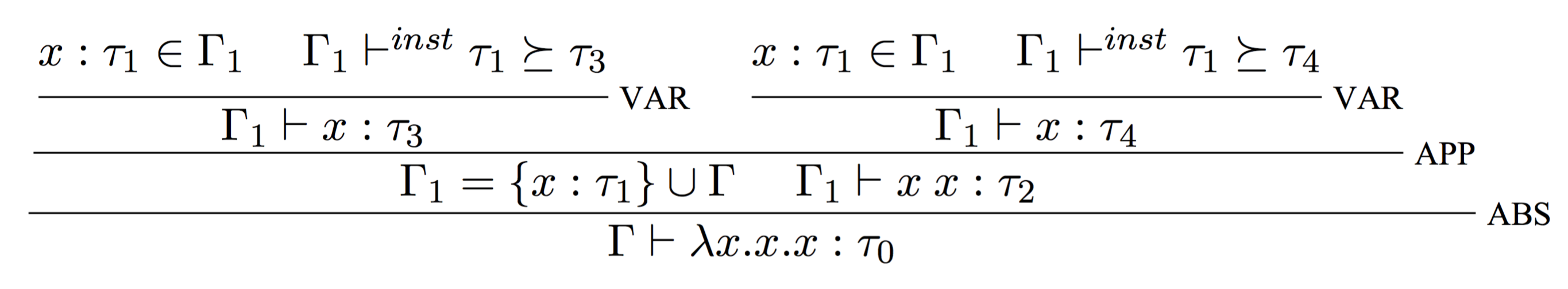
根据证明树，我们得到了如下约束：

$$\begin{align*} \tau_{0} & = \tau_{1}\rightarrow\tau_{2} \\ \tau_{3} & = \tau_{4}\rightarrow\tau_{2} \\ \tau_{1} & = \tau_{3} \\ \tau_{1} & = \tau_{4} \end{align*}$$

然后对约束进行unify:

$$\begin{align*} \{\tau_{0} = \tau_{1}\rightarrow\tau_{2},\ \tau_{3} = \tau_{4}\rightarrow\tau_{2},\ \tau_{1} = \tau_{3},\ \tau_{1} = \tau_{4}\}[\tau_{1}\mapsto\tau_{4}] \\ \Rightarrow \{\tau_{0} = \tau_{4}\rightarrow\tau_{2},\ \tau_{3} = \tau_{4}\rightarrow\tau_{2},\ \tau_{4} = \tau_{3}\}[\tau_{3}\mapsto\tau_{4}] \\ \Rightarrow \{\tau_{0} = \tau_{4}\rightarrow\tau_{2},\ \tau_{4} = \tau_{4}\rightarrow\tau_{2}\} \end{align*}$$

现在，规则集合里，出现了$\tau_{4} = \tau_{4}\rightarrow\tau_{2}$这样带有递归规则的等式，这明显不符合unify规则。从而推演过程失败。

究其原因，是因为$\lambda$的参数$x$是个monotype，在表达式$x\ x$中的两次出现，都必然是同一种类型，而这样的约束肯定无法支持$x\ x$的语义。

在HM类型系统下，一个$\lambda$的参数和结果类型都是monotype，但这与函数自身的类型是否是个polytype没有关系。