---

史瓦西时空中粒子的运动

作者: 刘祥干 2013301020107 物基二班
摘要: 本文简要介绍广义相对论中史瓦西时空下粒子的运动.讨论了轨道分类,水星进动,光线弯折和黑洞内外粒子运动的时间问题.并给出一些简单的物理图像.
关键词: 史瓦西时空 轨道 水星进动 黑洞

一.介绍

1915年,爱因斯坦发表了他的广义相对论场方程,革新了人们对时空的认知(由于场方程的高度复杂和非线性,严格的解析解目前只有几类).随后一年,史瓦西给出了场方程的静态对称真空解,这是爱因斯坦场方程的第一个严格解,用这个解,可以算出著名的三大验证的数学结果,还可以研究最简单的黑洞---史瓦西黑洞的构造.在本文中,我们给出史瓦西时空中粒子运动的一般规律,和轨道的分类.并简单地给出水星进动的一些简单图景,以及简单讨论史瓦西黑洞内外自由落体粒子的固有时和坐标时.

二.正文

1.史瓦西时空中粒子的运动方程

真空爱因斯坦场方程为:

$$R_{ab}-\frac{1}{2}g_{ab}R=0$$
史瓦西解为:
$$ds^2=-(1-\frac{2M}{r})dt^2+\frac{1}{(1-\frac{2M}{r})}dr^2+r^2(d\theta^2+sin^2\theta d\phi^2)$$
结合测底线方程可以得出粒子的运动方程,但是这样做比较复杂,简单的办法是利用拉式量找出守恒量.易写出史瓦西时空中粒子的拉式量为:
$$L=-\frac{1}{2}g_{ab}\dot{x}^a\dot{x}^b=\frac{1}{2}[(1-\frac{2M}{r})\dot{t}^2-\frac{1}{(1-\frac{2M}{r})}\dot{r}^2-r^2\dot{\theta}^2-r^2sin^2\theta \dot{\phi}^2]$$
易知存在两个守恒量:
$$E=\frac{\partial L}{\partial\dot{t}}=(1-\frac{2M}{r})\frac{dt}{d\lambda}$$
$$J=-\frac{\partial L}{\partial \dot{\phi}}=r^2sin^2\theta\frac{d\phi}{d\lambda}$$
此即能量守恒和角动量守恒,加上四速归一化条件:$g_{ab}u^au^b=-k$
即可得出三个运动方程:
$$\frac{dt}{d\lambda}=\frac{E}{(1-\frac{2M}{r})}$$
$$\frac{d\phi}{d\lambda}=\frac{J}{r^2}$$
$$(\frac{dr}{d\lambda})^2=E^2-(1-\frac{2M}{r})(k+\frac{J^2}{r^2})$$
由这三个基本运动方程,基本上可以求解出粒子在史瓦西时空中的一般运动.

2.运动轨道的分类

类似牛顿力学里面有心力场的做法,可以定义有效势,即

$$V(r)=\frac{1}{2}(1-\frac{2M}{r})(k+\frac{J^2}{r^2})$$
则径向运动为: $$\frac{1}{2}(\frac{dr}{d\lambda})^2+V(r)=\frac{1}{2}E^2$$
做为对比,我们写出牛顿力学中万有引力的有效势: $$V(r)=\frac{1}{2}(1-\frac{2M}{r})k+\frac{1}{2}\frac{J^2}{r^2}$$
可以看出,史瓦西解对经典的牛顿引力的修正就是多加了$-MJ^2/r^3$项
下面我们画出不同角动量对应的V-r图像.取J=M=1

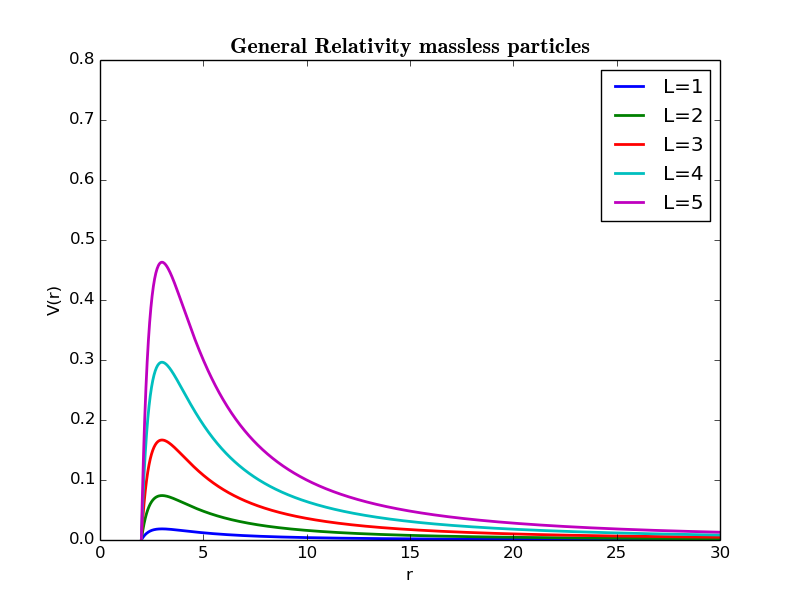
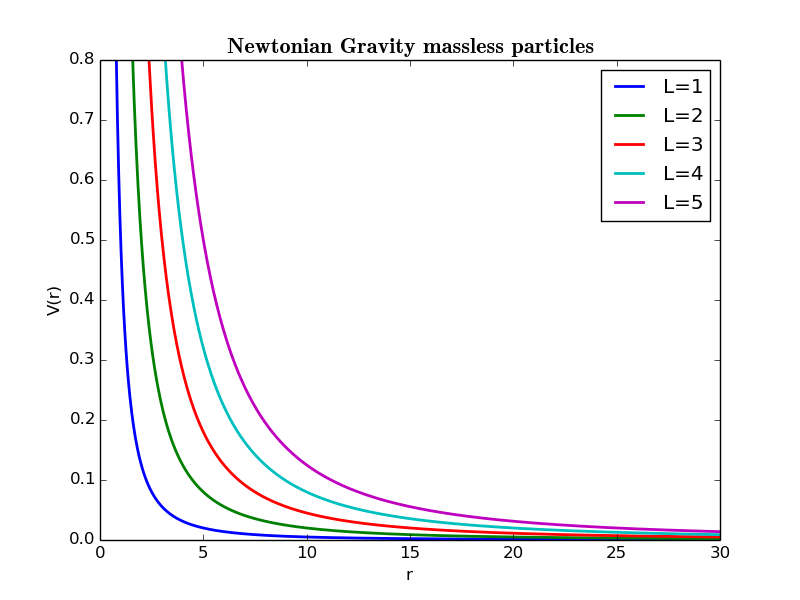
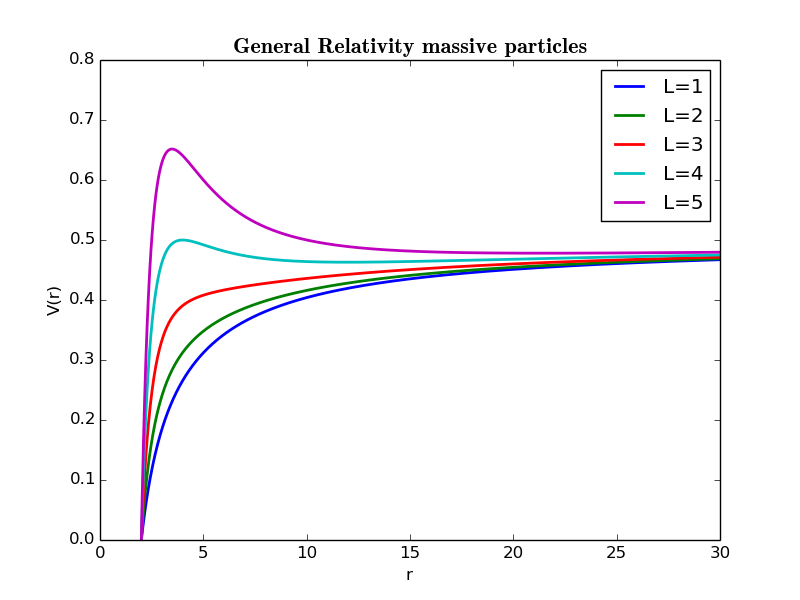
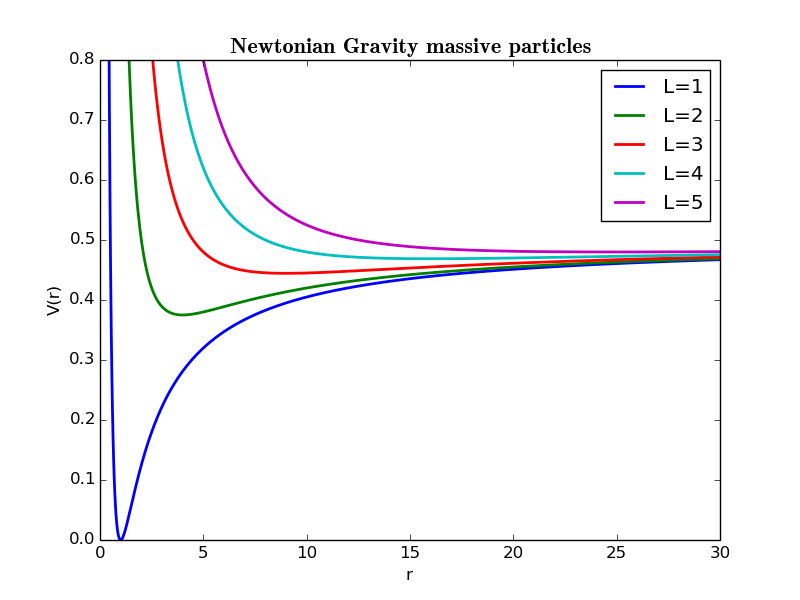
   对于有质量的粒子可以看出,J<3时,无论E多大,粒子只会被力心吸收,即不存在稳定的闭合轨道；3<J<4时,存在束缚态和吸收态.取决于具体E的大小；4<J时,存在束缚态,散射态和吸收态,取决于具体E的大小. 对于无质量粒子(如光子)可以类似讨论.

由$\frac{dV}{dr}=0$,易求出稳定圆轨道的大小.可知最小的圆轨道半径r=3M,3M<r<6M时,存在不稳定的圆轨道,而在r>6M时,存在稳定的圆轨道.

3.水星进动

水星的进动问题已在第十一次作业中有详细讨论,这里我们只给出其运动图像.
由三个基本的运动方程,从中消去$\lambda$即可得到$r-\phi$满足的微分方程:

$$\frac{d^2u}{d\phi^2}+u=(\frac{M}{J})^2+3u^2$$
其中,$u=M/r$.
这是非线性微分方程,可以用欧拉方法求解具体的运动轨道代码2:

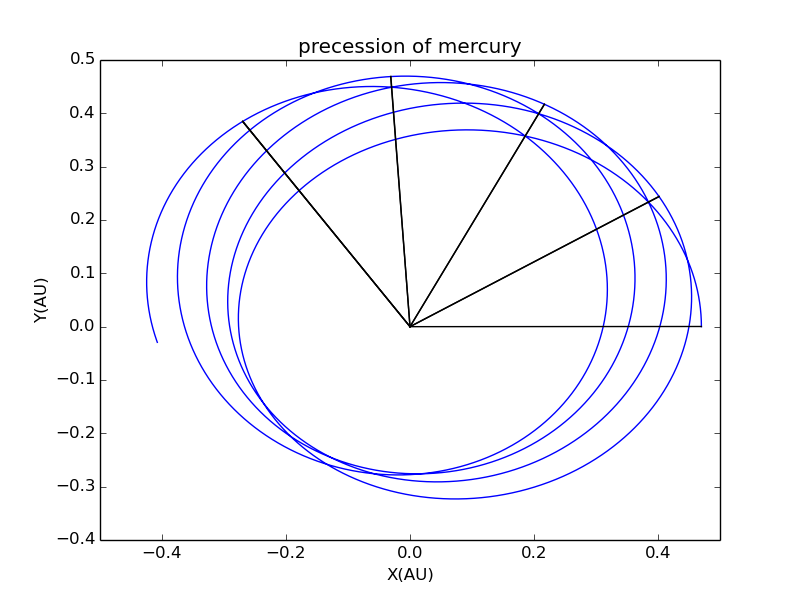
可以明显看出进动轨迹.

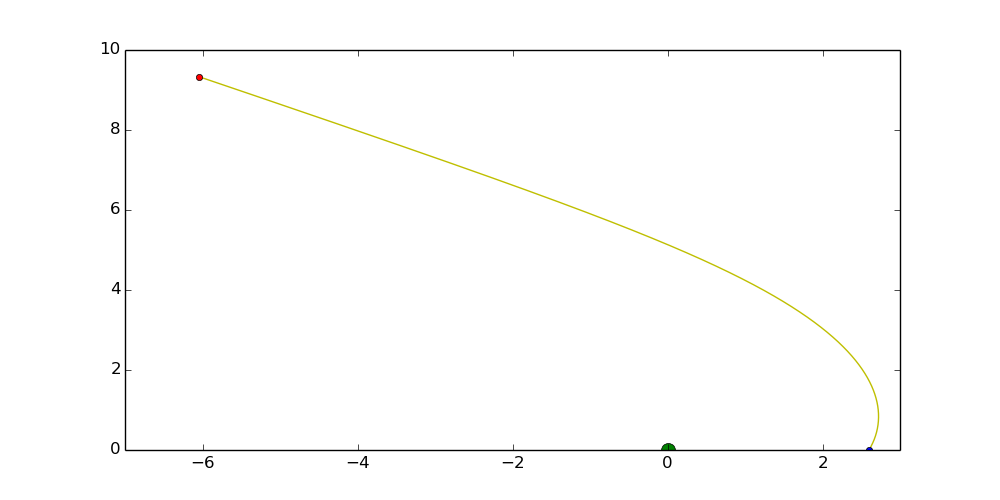
4.光线弯折

广义相对论的另一个有趣的现象是引力场中的光线弯折现象.
对于光线,运动方程中的参数k=0,同样可以用数值解法求解.
我们给出其简单的物理图像代码:

5.史瓦西黑洞中旅行者的时间

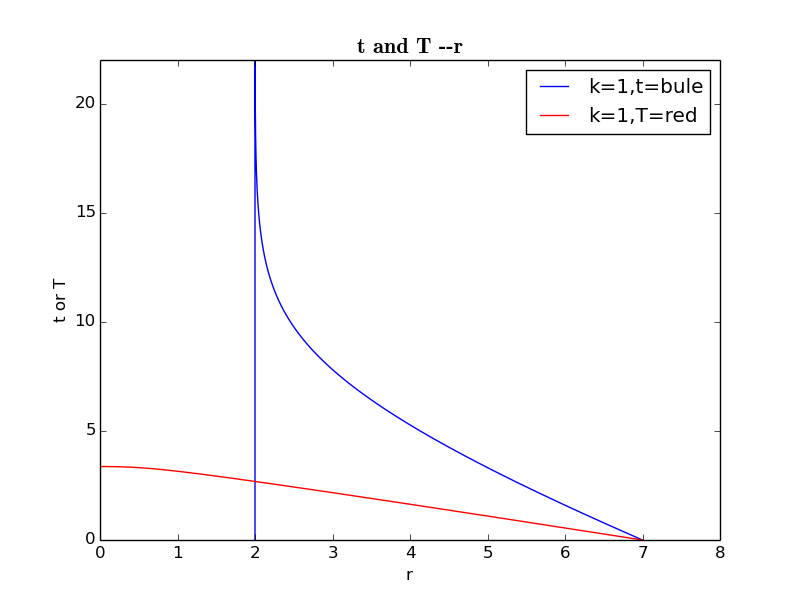
史瓦西度规在视界(r=2M)处存在坐标奇异性,此奇异性将史瓦西时空分成两个部分,各用一个史瓦西坐标描写.从三个基本的运动方程可知,在洞外一点$r_0$向黑洞自由下落的粒子,坐标时t与径向r的关系为:

$$dt=\frac{-E}{\sqrt {E^2-(1-2M/r)(1+J^2/r^2)}}\frac{rdr}{r-2M}$$
其固有时$\tau$与径向r关系为:
$$d\tau=\frac{dr}{\sqrt {E^2-(1-2M/r)(1+J^2/r^2)}}$$
E是常数,解释为粒子在无穷远处时的能量.容易用数值求解其运动代码3:

类似地,可以得到黑洞内的关系代码4:

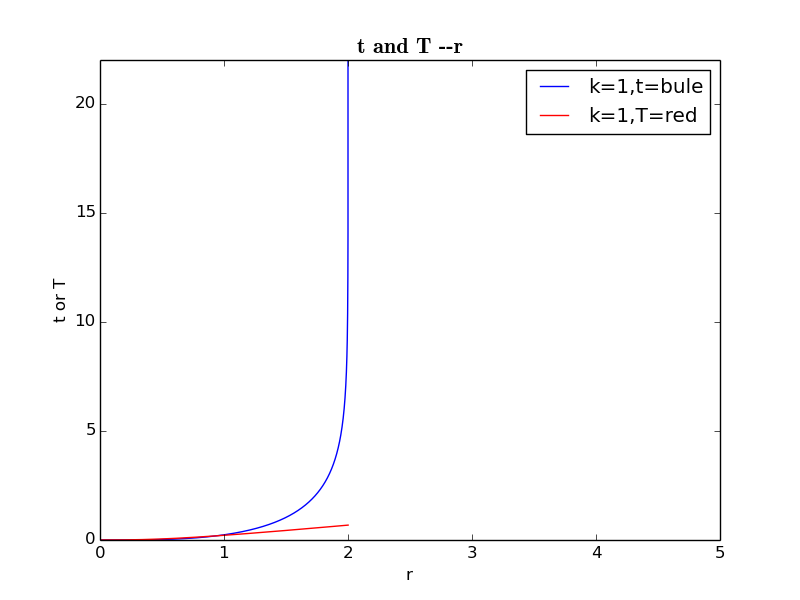
容易看出坐标时t在r=2M趋于无穷大.这可解释为:在无穷远处的静止观测者观察粒子运动到黑洞表面附近时几乎静止了,要花无穷多的时间抵达视界,更不能穿越视界,但是实际上,粒子自身穿越过视界时毫无异常,所花时间相比坐标时短很多很多,即粒子在有限时间内可以落进黑洞,从图中那条光滑的红线即可看出.

三.结论

详见正文.
综上可知其史瓦西时空中粒子运动与经典牛顿力学中有一定相似,又有很多不同的地方,例如水星进动,光线弯折和黑洞这些非常有趣的内容.而现在这些结论都已经被实验很好的验证了.

四.致谢

感谢何牧野等同学的帮助.

五.论文引用

1<<广义相对论基础>>.赵峥,刘文彪
2<< N.J. Giordano,H. Nakanishi.Computational Physics(second edition>>（影印版）.清华大学出版社