[关闭]
@attack666 2020-12-18T10:42:15.000000Z 字数 75842 阅读 1491

ACM模板

哈尔滨工业大学(威海)

ACM模板

序列数据结构

ST表

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 2e6 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M;
  11. int a[MAXN][21], lg2[MAXN];
  12. int Query(int l, int r) {
  13.     int k = lg2[r - l + 1];
  14.     return max(a[l][k], a[r - (1 << k) + 1][k]);
  15. }
  16. int main() {
  17.     N = read(); M = read();
  18.     for(int i = 1; i <= N; i++) a[i][0] = read(), lg2[i] = (i == 1 ? 0 : lg2[i >> 1] + 1);
  19.     for(int j = 1; j <= 20; j++)
  20.         for(int i = 1; i + (1 << j) - 1 <= N; i++) 
  21.             a[i][j] = max(a[i][j - 1], a[i + (1 << j - 1)][j - 1]); 
  22.     while(M--) {
  23.         int l = read(), r = read();
  24.         cout << Query(l, r) << '\n';
  25.     }
  26.     return 0;
  27. }

普通线段树

如题，已知一个数列，你需要进行下面三种操作：

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 1e6 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M, mod;
  11. #define ls k << 1 
  12. #define rs k << 1 | 1
  13. int add(int x, int y) {return (x + y + mod) % mod;}
  14. int mul(int x, int y) {return 1ll * x * y % mod;}
  15. void mul2(int &x, int y) {x = 1ll * x * y % mod;}
  16. void add2(int &x, int y) {x = (x + y + mod) % mod;}
  17. int sum[MAXN], tagm[MAXN], taga[MAXN], len[MAXN];
  18. void ps(int k, int addv, int mulv) {
  19.     mul2(sum[k], mulv); add2(sum[k], mul(len[k], addv));
  20.     mul2(taga[k], mulv); add2(taga[k], addv);
  21.     mul2(tagm[k], mulv);
  22. }
  23. void pushdown(int k) {
  24.     if((!taga[k]) && (tagm[k] == 1)) return ;
  25.     ps(ls, taga[k], tagm[k]);
  26.     ps(rs, taga[k], tagm[k]);
  27.     taga[k] = 0; tagm[k] = 1;
  28.     return ;
  29. }
  30. void update(int k) {
  31.     sum[k] = add(sum[ls], sum[rs]);
  32. }
  33. void Build(int k, int l, int r) {
  34.     tagm[k] = 1; len[k] = r - l + 1;
  35.     if(l == r) {sum[k] = read(); return ;}
  36.     int mid = (l + r) >> 1;
  37.     Build(ls, l, mid); Build(rs, mid + 1, r);
  38.     update(k);
  39. }
  40. void IntMul(int k, int l, int r, int ql, int qr, int v) {
  41.     if(ql <= l && r <= qr) {ps(k, 0, v); return ;}
  42.     pushdown(k);
  43.     int mid = (l + r) >> 1;
  44.     if(ql <= mid) IntMul(ls, l, mid, ql, qr, v);
  45.     if(qr  > mid) IntMul(rs, mid + 1, r, ql, qr, v);
  46.     update(k);
  47. }
  48. void IntAdd(int k, int l, int r, int ql, int qr, int v) {
  49.     if(ql <= l && r <= qr) {ps(k, v, 1); return ;}
  50.     pushdown(k);
  51.     int mid = (l + r) >> 1;
  52.     if(ql <= mid) IntAdd(ls, l, mid, ql, qr, v);
  53.     if(qr  > mid) IntAdd(rs, mid + 1, r, ql, qr, v);
  54.     update(k);
  55. }
  56. int Query(int k, int l, int r, int ql, int qr) {
  57.     if(ql <= l && r <= qr) return sum[k];
  58.     pushdown(k);
  59.     int mid = (l + r) >> 1, ans = 0;
  60.     if(ql <= mid) add2(ans, Query(ls, l, mid, ql, qr));
  61.     if(qr  > mid) add2(ans, Query(rs, mid + 1, r, ql, qr));
  62.     return ans;
  63. }
  64. int main() {
  65.     N = read(); M = read(); mod = read();
  66.     Build(1, 1, N);
  67.     while(M--) {
  68.         int opt = read(), l = read(), r = read();
  69.         if(opt == 1) {
  70.             int val = read();
  71.             IntMul(1, 1, N, l, r, val);
  72.         } else if(opt == 2) {
  73.             int val = read();
  74.             IntAdd(1, 1, N, l, r, val);//puts("a");
  75.         } else {
  76.             cout << Query(1, 1, N, l, r) << '\n';
  77.         }
  78.     }
  79.     return 0;
  80. }

动态开点线段树

蒟蒻DCrusher不仅喜欢玩扑克，还喜欢研究数列
题目描述
DCrusher有一个数列，初始值均为0，他进行N次操作，每次将数列[a,b)这个区间中所有比k小的数改为k，他想知
道N次操作后数列中所有元素的和。他还要玩其他游戏，所以这个问题留给你解决。

  1. #include<bits/stdc++.h> 
  2. #define LL long long 
  3. using namespace std;
  4. const int MAXN = 8e6 + 10, INF = 1e9 + 10;
  5. template <typename A, typename B> inline bool chmin(A &a, B b){if(a > b) {a = b; return 1;} return 0;}
  6. template <typename A, typename B> inline bool chmax(A &a, B b){if(a < b) {a = b; return 1;} return 0;}
  7. inline int read() {
  8.     char c = getchar(); int x = 0, f = 1;
  9.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  10.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  11.     return x * f;
  12. }
  13. int N, rt, ls[MAXN], rs[MAXN], mx[MAXN], tot;
  14. void IntMax(int &k, int l, int r, int ll, int rr, int val) {
  15.     if(!k) k = ++tot;
  16.     if(ll <= l && r <= rr) {chmax(mx[k], val); return ;}
  17.     int mid = l + r >> 1;
  18.     if(ll <= mid) IntMax(ls[k], l, mid, ll, rr, val);
  19.     if(rr  > mid) IntMax(rs[k], mid + 1, r, ll, rr, val);
  20. }
  21. LL Query(int k, int l, int r, int val) {
  22.     chmax(mx[k], val); chmax(val, mx[k]);
  23.     if(l == r) return mx[k];
  24.     int mid = l + r >> 1;LL ans = 0;
  25.     if(ls[k]) ans += Query(ls[k], l, mid, val);
  26.     else ans += (mid - l + 1) * mx[k];
  27.     if(rs[k]) ans += Query(rs[k], mid + 1, r, val);
  28.     else ans += (r - mid) * mx[k];
  29.     return ans;
  30. }
  31. signed main() {
  32.     N = read();
  33.     for(int i = 1; i <= N; i++) {
  34.         int l = read(), r = read() - 1, k = read();
  35.         IntMax(rt, 1, INF, l, r, k);
  36.     }
  37.     printf("%lld\n", Query(rt, 1, INF, 0));
  38.     return 0;
  39. }

树状数组

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define lb(x) (x & (-x))
  4. const int MAXN = 2e6 + 10;
  5. inline int read() {
  6.     char c = getchar(); int x = 0, f = 1;
  7.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  8.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  9.     return x * f;
  10. }
  11. int N, M;
  12. int a[MAXN];
  13. void add(int p, int v) {
  14.     while(p <= N) a[p] += v, p += lb(p);
  15. }
  16. int Que(int x) {
  17.     int ans = 0;
  18.     while(x) ans += a[x], x -= lb(x);
  19.     return ans;
  20. }
  21. int Query(int l, int r) {
  22.     return Que(r) - Que(l - 1);
  23. }
  25. int main() {    
  26. #ifndef ONLINE_JUDGE
  27.     freopen("a.in", "r", stdin);
  28.     freopen("a.out", "w", stdout);
  29. #endif
  30.     N = read(); M = read();
  31.     for(int i = 1; i <= N; i++) add(i, read());
  32.     while(M--) {
  33.         int opt = read();
  34.         if(opt == 1) {
  35.             int x = read(), val = read();
  36.             add(x, val);
  37.         } else {
  38.             int l = read(), r = read();
  39.             cout << Query(l, r) << '\n';
  40.         }
  41.     }
  42.     return 0;
  43. }

主席树

  1. #include<bits/stdc++.h>
  2. #define Pair pair<int, int>
  3. #define MP make_pair
  4. #define fi first
  5. #define se second 
  6. #define pb push_back
  7. using namespace std;
  8. const int MAXN = 4e6 + 10, INF = 1e9 + 10;
  9. inline int read() {
  10.     char c = getchar(); int x = 0, f = 1;
  11.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  12.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  13.     return x * f;
  14. }
  15. int N, M, a[MAXN], date[MAXN], num;
  16. void Des() {
  17.     for(int i = 1; i <= N; i++) date[i] = a[i];
  18.     sort(date + 1, date + N + 1);
  19.     num = unique(date + 1, date + N + 1) - date - 1;
  20.     for(int i = 1; i <= N; i++) a[i] = lower_bound(date + 1, date + num + 1, a[i]) - date;
  21. }
  22. int ls[MAXN], rs[MAXN], siz[MAXN], rt[MAXN], tot;
  23. void insert(int &x, int pre, int l, int r, int pos) {
  24.     x = ++tot;
  25.     ls[x] = ls[pre]; rs[x] = rs[pre]; siz[x] = siz[pre] + 1;
  26.     if(l == r) return ;
  27.     int mid = (l + r) >> 1;
  28.     if(pos <= mid) rs[x] = rs[pre], insert(ls[x], ls[pre], l, mid, pos);
  29.     else ls[x] = ls[pre], insert(rs[x], rs[pre], mid + 1, r, pos); 
  30. }
  31. int Query(int rl, int rr, int l, int r, int k) {
  32.     //cout << siz[k] << '\n';
  33.     if(l == r) return l;
  34.     int mid = (l + r) >> 1, usd = siz[ls[rr]] - siz[ls[rl]];
  35.     if(k <= usd) return Query(ls[rl], ls[rr], l, mid, k);
  36.     else return Query(rs[rl], rs[rr], mid + 1, r, k - usd);
  37. }
  38. int main() {
  39.     N = read(); M = read();
  40.     for(int i = 1; i <= N; i++) a[i] = read();
  41.     Des();
  43.     for(int i = 1; i <= N; i++) insert(rt[i], rt[i - 1], 1, num, a[i]);
  45.     while(M--) {
  46.         int l = read(), r = read(), k = read();
  47.         cout << date[Query(rt[l - 1], rt[r], 1, num, k)] << '\n';
  48.     }
  49.     return 0;
  50. }

树上数据结构

K-D tree

  1. #include<bits/stdc++.h>
  2. #define chmin(x, y) (x = x < y ? x : y)
  3. #define chmax(x, y) (x = x > y ? x : y)
  4. #define ls(x) T[k].ls
  5. #define rs(x) T[k].rs
  6. #define double long double 
  7. const double alpha(acos(-1) / 5);
  8. const double cosa(cos(alpha));
  9. const double sina(sin(alpha));
  10. using namespace std;
  11. const int MAXN = 1e6 + 10;
  12. const double INF = 1e12 + 10, eps = 1e-11;
  13. inline int read() {
  14.     char c = getchar(); int x = 0, f = 1;
  15.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  16.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  17.     return x * f;
  18. }
  19. int N, WD, root, tot, num, ans[MAXN];
  20. struct Point {
  21.     double x[2], r;
  22.     int id;
  23.     bool operator < (const Point &rhs) const {
  24.         return rhs.x[WD] - x[WD] > eps; 
  25.     }
  26.     double operator [] (const int d) {
  27.         return x[d];
  28.     }
  29. }P[MAXN];
  30. int comp(const Point &a, const Point b) {
  31.     return a.r == b.r ? a.id < b.id : a.r > b.r;
  32. }
  33. struct Node {
  34.     int ls, rs, id;
  35.     double mx[2], mi[2];
  36.     Point p;
  37. }T[MAXN];
  38. void update(int k) {
  39.     for(int i = 0; i <= 1; i++) {
  40.         if(!ans[T[k].id]) T[k].mi[i] = T[k].p[i] - T[k].p.r, T[k].mx[i] = T[k].p[i] + T[k].p.r;
  41.         else T[k].mi[i] = INF, T[k].mx[i] = -INF;
  42.         if(ls(k)) chmin(T[k].mi[i], T[ls(k)].mi[i]), chmax(T[k].mx[i], T[ls(k)].mx[i]);
  43.         if(rs(k)) chmin(T[k].mi[i], T[rs(k)].mi[i]), chmax(T[k].mx[i], T[rs(k)].mx[i]);
  44.     }   
  45. }
  46. int Build(int l, int r, int wd) {
  47.     if(l > r) return 0;
  48.     WD = wd; int mid = (l + r) >> 1, k = ++tot;
  49.     nth_element(P + l, P + mid, P + r + 1);
  50.     T[k].p = P[mid];  T[k].id = P[mid].id; 
  51.     T[k].ls = Build(l, mid - 1, wd ^ 1) ;
  52.     T[k].rs = Build(mid + 1, r, wd ^ 1);
  53.     update(k);
  54.     return k;
  55. }
  56. double sqr(double x) {
  57.     return x * x;
  58. }
  59. bool judge(Point a, Point b) {
  60.     double tmp = sqr(a[0] - b[0]) + sqr(a[1] - b[1]);
  61.     return sqr(a.r + b.r) + eps - tmp > 0;
  62. }
  63. bool pd(int k, Point a) {
  64.     for(int i = 0; i <= 1; i++) 
  65.         if((a[i] + a.r + eps < T[k].mi[i]) || (a[i] - a.r - eps > T[k].mx[i])) return 1;
  67.     return 0;
  68. }
  69. void Delet(int k, Point a) {
  70.     if(pd(k, a)) return ;
  71.     if(!ans[T[k].id] && judge(T[k].p, a)) ans[T[k].id] = a.id, T[k].p.r = -INF, num++;
  72.     if(ls(k)) Delet(ls(k), a);
  73.     if(rs(k)) Delet(rs(k), a);
  74.     update(k);
  75. }
  76. int main() {
  77.     //freopen("a.in", "r", stdin);
  78.     N = read();
  79.     for(int i = 1; i <= N; i++) {
  80.         double x = read(), y = read(), tx = x * cosa - y * sina, ty = x * sina + y * cosa;
  81.         P[i].x[0] = x; P[i].x[1] = y; P[i].r = read(), P[i].id = i;
  82.     }
  83.     root = Build(1, N, 0);
  84.     sort(P + 1, P + N + 1, comp);
  85.     for(int i = 1; i <= N; i++) if(!ans[P[i].id]) Delet(root, P[i]);
  86.     for(int i = 1; i <= N; i++) printf("%d ", ans[i]);
  87.     return 0;
  88. }

普通平衡树

  1. #include<bits/stdc++.h>
  2. template <typename A, typename B> inline bool chmax(A &x, B y) {return x < y ? x = y, 1 : 0;}
  3. template <typename A, typename B> inline bool chmin(A &x, B y) {return x > y ? x = y, 1 : 0;}
  4. using namespace std;
  5. const int MAXN = 1e6 + 10, INF = 1e9 + 10;
  6. inline int read() {
  7.     char c = getchar(); int x = 0, f = 1;
  8.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  9.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  10.     return x * f;
  11. }
  12. int N;
  13. #define ls(k) ch[k][0]
  14. #define rs(k) ch[k][1]
  15. int ch[MAXN][2], fa[MAXN], rev[MAXN], siz[MAXN], val[MAXN], tot, root;
  16. int newnode(int _fa, int _val) {
  17.     int cur = ++tot;
  18.     fa[cur] = _fa; val[cur] = _val; rev[cur] = siz[cur] = 1;
  19.     return cur;
  20. }
  21. bool ident(int x) {
  22.     return ch[fa[x]][1] == x;
  23. }
  24. void connect(int x, int _fa, int tag) {
  25.     fa[x] = _fa; ch[_fa][tag] = x;
  26. }
  27. void update(int k) {
  28.     siz[k] = siz[ls(k)] + siz[rs(k)] + rev[k];
  29. }
  30. void rotate(int x) {
  31.     int y = fa[x], r = fa[y], yson = ident(x), rson = ident(y);
  32.     int B = ch[x][yson ^ 1];
  33.     connect(B, y, yson);
  34.     connect(x, r, rson);
  35.     connect(y, x, yson ^ 1);
  36.     update(y); update(x);
  37. }
  38. void splay(int x, int to) {//tag
  39.     if(x < 0) {
  40.         puts("G");
  41.     }
  42.     while(fa[x] != to) {
  43.         int y = fa[x];
  44.         if(fa[y] == to) rotate(x);
  45.         else if(ident(x) == ident(y)) rotate(x), rotate(x);
  46.         else rotate(y), rotate(x);
  47.     }
  48.     if(!to) root = x;
  49. }
  50. void Insert(int v) {
  51.     int now = root;
  52.     if(!now) {root = newnode(0, v);  return ;}
  53.     while(now) {
  54.         siz[now]++;
  55.         if(val[now] == v) {rev[now]++; splay(now, 0); return ;}
  56.         int nxt = v > val[now];
  57.         if(!ch[now][nxt]) {ch[now][nxt] = newnode(now, v); splay(now, 0); return ;}
  58.         now = ch[now][nxt];
  59.     }
  60.     splay(now, 0);
  61. }
  62. int find(int v) {
  63.     int now = root;
  64.     while(now) {
  65.         if(val[now] == v) {splay(now, 0); return now;}
  66.         now = ch[now][v > val[now]];
  67.     }
  68.     puts("can't find v");
  69.     assert(1 == 2);
  70. }
  71. int rak(int v) {
  72.     int pos = find(v);
  73.     return siz[ls(pos)] + 1;
  74. }
  75. int kth(int k) {
  76.     int now = root;
  77.     while(now) {
  78.         int used = siz[now] - siz[rs(now)];
  79.         if(k > siz[ls(now)] && k <= used) return val[now];
  80.         else if(k <= siz[ls(now)]) now = ls(now);
  81.         else k -= used, now = rs(now);
  82.     }
  83.     puts("can't find kth");
  84.     assert(1 == 2);
  85. }
  86. int Pre(int v) {
  87.     int now = root, ans = 0;
  88.     while(now) {
  89.         if(val[now] < v) ans = now;
  90.         int nxt = (v <= val[now] ? 0 : 1);
  91.         now = ch[now][nxt];
  92.     }
  93.     assert(ans);
  94.     return ans;
  95. }
  96. int Nxt(int v) {
  97.     int now = root, ans = 0;
  98.     while(now) {
  99.         if(val[now] > v) ans = now;
  100.         int nxt = (v < val[now] ? 0 : 1);
  101.         now = ch[now][nxt];
  102.     }
  103.     assert(ans);
  104.     return ans;
  105. }
  106. void delet(int x) {
  107.     int pr = Pre(x), nx = Nxt(x);
  108.     splay(pr, 0); splay(nx, pr);
  109.     int pos = ch[nx][0];
  110.     if(rev[pos] > 1) rev[pos]--, splay(pos, 0);
  111.     else ch[nx][0] = 0, splay(nx, 0);
  112. }
  113. int main() {
  114.     N = read();
  115.     Insert(-INF); Insert(INF);
  116.     while(N--) {
  117.         int opt = read(), x = read();
  118.         if(opt == 1) Insert(x);
  119.         else if(opt == 2) delet(x);
  120.         else if(opt == 3) cout << rak(x) - 1 << '\n';
  121.         else if(opt == 4) cout << kth(x + 1) << '\n';
  122.         else if(opt == 5) cout << val[Pre(x)] << '\n';
  123.         else cout << val[Nxt(x)] << '\n';
  124.     }
  125.     return 0;
  126. }

LCT

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 1e5 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M, a[MAXN];
  11. #define ls(k) ch[k][0]
  12. #define rs(k) ch[k][1]
  13. int ch[MAXN][2], rev[MAXN], fa[MAXN], sum[MAXN], st[MAXN];
  14. void update(int k) {
  15.     sum[k] = sum[ls(k)] ^ sum[rs(k)] ^ a[k];
  16. }
  17. void pushdown(int k) {
  18.     if(!rev[k]) return ;
  19.     swap(ls(k), rs(k));
  20.     rev[ls(k)] ^= 1;
  21.     rev[rs(k)] ^= 1;
  22.     rev[k] = 0;
  23. }
  24. bool isroot(int x) {
  25.     return ch[fa[x]][0] != x && ch[fa[x]][1] != x;
  26. }
  27. bool ident(int x) {
  28.     return ch[fa[x]][1] == x;
  29. }
  30. void connect(int x, int _fa, int tag) {
  31.     fa[x] = _fa; ch[_fa][tag] = x;
  32. }
  33. void rotate(int x) {
  34.     int y = fa[x], r = fa[y], yson = ident(x), rson = ident(y);
  35.     int b = ch[x][yson ^ 1];
  36.     fa[x] = r;
  37.     if(!isroot(y)) connect(x, r, rson);//×¢Òâ¸üеÄÏȺó˳Ðò 
  38.     connect(b, y, yson);
  39.     connect(y, x, yson ^ 1);
  40.     update(y); update(x);
  41. }
  42. void splay(int x) {
  43.     int y = x, top =0;
  44.     st[++top] = y;
  45.     while(!isroot(y)) st[++top] = (y = fa[y]);
  46.     while(top) pushdown(st[top--]);
  47.     for(int y = fa[x]; !isroot(x); rotate(x), y = fa[x])
  48.         if(!isroot(y))
  49.             rotate(ident(x) == ident(y) ? y : x);
  50. }
  51. void access(int x) {
  52.     for(int y = 0; x ; x = fa[y = x])
  53.         splay(x), rs(x) = y, update(x);
  54. }
  55. void makeroot(int x) {
  56.     access(x);
  57.     splay(x);
  58.     rev[x] ^= 1;
  59. }
  60. int findroot(int x) {
  61.     access(x); splay(x);
  62.     pushdown(x);
  63.     while(ls(x)) pushdown(ls(x)), x = ls(x);
  64.     splay(x);
  65.     return x;
  66. }
  67. void link(int x, int y) {
  68.     makeroot(x);
  69.     if(findroot(y) == x) return ;
  70.     fa[x] = y;
  71. }
  72. void cut(int x, int y) {
  73.     makeroot(x);
  74.     if(findroot(y) != x || fa[y] != x || ls(y)) return ;
  75.     fa[y] = 0; rs(x) = 0;
  76.     update(x);
  77. }
  78. void Modify(int x, int v) {
  79.     splay(x);
  80.     a[x] = v;
  81. }
  82. int Query(int x, int y) {
  83.     makeroot(x);
  84.     access(y); splay(y);
  85.     return sum[y];
  86. }
  87. int main() {
  88.     N = read(); M = read();
  89.     for(int i = 1; i <= N; i++) a[i] = read();
  90.     while(M--) {
  91.         int opt = read(), x = read(), y = read();
  92.         if(opt == 0) cout << Query(x, y) << '\n';
  93.         else if(opt == 1) link(x, y);
  94.         else if(opt == 2) cut(x, y);
  95.         else Modify(x, y);
  96.     }
  97.     return 0;
  98. }

点分治

给定一棵有n个点的树，询问树上距离为k的点对是否存在。

  1. #include<bits/stdc++.h>
  2. #define Pair pair<int, int>
  3. #define MP make_pair
  4. #define fi first
  5. #define se second 
  6. #define pb push_back 
  7. using namespace std;
  8. const int MAXN = 1e6 + 10, INF = 1e9 + 10;
  9. inline int read() {
  10.     int x; 
  11.     cin >> x;
  12.     return x;
  13. }
  14. int N, M;
  15. vector<Pair> v[MAXN];
  16. void AE(int x, int y, int z) {
  17.     v[x].pb(MP(y, z));
  18. }
  19. Pair qr[MAXN];
  20. int Root, Sum, mx[MAXN], siz[MAXN], vis[MAXN];
  21. void FindRoot(int x, int fa) {
  22.     if(vis[x]) return ;
  23.     siz[x] = 1; mx[x] = 0;
  24.     for(int i = 0; i < v[x].size(); i++) {
  25.         int to = v[x][i].fi;
  26.         if(to == fa || vis[to]) continue;
  27.         FindRoot(to, x);
  28.         siz[x] += siz[to];
  29.         mx[x] = max(mx[x], siz[to]);
  30.     }
  31.     mx[x] = max(mx[x], Sum - siz[x]);
  32.     if(mx[x] < mx[Root]) Root = x;
  33. }
  34. bool tim[10000001];
  35. int cnt, val[MAXN];
  36. void add(int x, int fa, int w) {
  37.     val[++cnt] = w;
  38.     for(int i = 0; i < v[x].size(); i++) {
  39.         int to = v[x][i].fi;
  40.         if(to == fa || vis[to]) continue;
  41.         add(to, x, w + v[x][i].se);
  42.     }
  43. }
  44. void dfs(int x, int fa) {
  45.     tim[0] = 1; 
  46.     queue<int> q;
  47.     for(int i = 0; i < v[x].size(); i++) {
  48.         int to = v[x][i].fi;
  49.         if(to == fa || vis[to]) continue;
  50.         cnt = 0;
  51.         add(to, x, v[x][i].se);
  52.         //sort(val + 1, val + cnt + 1;
  53.         for(int j = 1; j <= cnt; j++)
  54.             for(int k = 1; k <= M; k++) {
  55.                 if(qr[k].fi >= val[j]) qr[k].se |= tim[qr[k].fi - val[j]];
  56.             }
  57.         for(int j = 1; j <= cnt; j++)
  58.             tim[val[j]] = 1, q.push(val[j]);
  59.     }
  60.     while(!q.empty()) tim[q.front()] = 0, q.pop();
  61.     vis[x] = 1; 
  62.     for(int i = 0; i < v[x].size(); i++) {
  63.         int to = v[x][i].fi;
  64.         if(to == fa || vis[to]) continue;
  65.         Sum = siz[to]; Root = 0; 
  66.         FindRoot(to, x);
  67.         dfs(Root, 0);
  68.     }
  69. }
  70. int main() {
  71.     //freopen("a.in", "r", stdin);
  72.     N = read(); M = read();
  73.     for(int i = 1; i < N; i++) {
  74.         int x = read(), y = read(), z = read();
  75.         AE(x, y, z); AE(y, x, z);
  76.     }
  77.     for(int i = 1; i <= M; i++) qr[i].fi = read();
  78.     Root = 0; mx[Root] = INF; Sum = N;
  79.     FindRoot(1, 0);
  80.     dfs(Root, 0);
  81.     for(int i = 1; i <= M; i++) 
  82.         puts(qr[i].se ? "AYE" : "NAY");
  83.     return 0;
  84. }

树链剖分

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 4e6 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M, R, mod;
  11. int a[MAXN], dep[MAXN], id[MAXN], rev[MAXN], fa[MAXN], siz[MAXN], son[MAXN], top[MAXN], tim;
  12. vector<int> v[MAXN];
  14. void dfs1(int x, int _fa) {
  15.     fa[x] = _fa;    
  16.     dep[x] = dep[fa[x]] + 1; 
  17.     siz[x] = 1; 
  18.     for(int i = 0; i < v[x].size(); i++) {
  19.         int to = v[x][i];
  20.         if(to == _fa) continue;
  21.         dfs1(to, x);
  22.         siz[x] += siz[to];
  23.         if(siz[to] > siz[son[x]]) son[x] = to;
  24.     }
  25. }
  26. void dfs2(int x, int topf) { 
  27.     top[x] = topf;
  28.     id[x] = ++tim;
  29.     rev[tim] = x;
  30.     if(!son[x]) return ;
  31.     dfs2(son[x], topf);
  32.     for(int i = 0; i < v[x].size(); i++) {
  33.         int to = v[x][i];
  34.         if(top[to]) continue;
  35.         dfs2(to, to);
  36.     }
  37. }
  38. #define ls k << 1
  39. #define rs k << 1 | 1
  40. int sum[MAXN], tag[MAXN], len[MAXN];
  41. void update(int k) {
  42.     sum[k] = (sum[ls] + sum[rs]) % mod;
  43. }
  44. void Build(int k, int l, int r) {
  45.     len[k] = r - l + 1; 
  46.     if(l == r) {sum[k] = a[rev[l]]; return ;}
  47.     int mid = (l + r) >> 1;
  48.     Build(ls, l, mid);
  49.     Build(rs, mid + 1, r);
  50.     update(k);
  51. }
  52. void ps(int k, int v) {
  53.     sum[k] = (sum[k] + 1ll * len[k] * v % mod) % mod;
  54.     tag[k] = (tag[k] + v) % mod;
  55. }
  56. void pushdown(int k) {
  57.     if(!tag[k]) return ;
  58.     ps(ls, tag[k]); ps(rs, tag[k]);
  59.     tag[k] = 0;
  60. }
  61. void Add(int k, int l, int r, int ql, int qr, int v) {
  62.     if(ql <= l && r <= qr) {ps(k, v); return ;}
  63.     int mid = (l + r) >> 1;
  64.     pushdown(k);
  65.     if(ql <= mid) Add(ls, l, mid, ql, qr, v);
  66.     if(qr  > mid) Add(rs, mid + 1, r, ql, qr, v);
  67.     update(k);
  68. }
  69. int Query(int k, int l, int r, int ql, int qr) {
  70.     if(ql <= l && r <= qr) return sum[k];
  71.     int mid = (l + r) >> 1, ans = 0;
  72.     pushdown(k);
  73.     if(ql <= mid) ans = (ans + Query(ls, l, mid, ql, qr)) % mod;
  74.     if(qr  > mid) ans = (ans + Query(rs, mid + 1, r, ql, qr)) % mod;
  75.     return ans;
  76. }
  77. void Tadd(int x, int y, int v) { 
  78.     while(top[x] ^ top[y]) {
  79.         if(dep[top[x]] < dep[top[y]]) swap(x, y);
  80.         Add(1, 1, N, id[top[x]], id[x], v);
  81.         x = fa[top[x]];
  82.     }
  83.     if(dep[x] > dep[y]) swap(x, y);
  84.     Add(1, 1, N, id[x], id[y], v);
  85. }
  86. int TQuery(int x, int y) {
  87.     int ans = 0;
  88.     while(top[x] ^ top[y]) {
  89.         if(dep[top[x]] < dep[top[y]]) swap(x, y);
  90.         ans = (ans + Query(1, 1, N, id[top[x]], id[x])) % mod;
  91.         x = fa[top[x]];
  92.     }
  93.     if(dep[x] > dep[y]) swap(x, y);
  94.     return (ans + Query(1, 1, N, id[x], id[y])) % mod;
  95. }
  96. int main() {
  97.     N = read(); M = read(); R = read(); mod = read();
  98.     for(int i = 1; i <= N; i++) a[i] = read();
  99.     for(int i = 1; i < N; i++) {
  100.         int x = read(), y = read();
  101.         v[x].push_back(y);
  102.         v[y].push_back(x);
  103.     }
  104.     dfs1(R, 0);
  105.     dfs2(R, R);
  106.     Build(1, 1, N);
  107.     while(M--) {
  108.         int opt = read();
  109.         if(opt == 1) {
  110.             int x = read(), y = read(), z = read();
  111.             Tadd(x, y, z); 
  112.         } else if(opt == 2) {
  113.             int x = read(), y = read();
  114.             cout << TQuery(x, y) << '\n';
  115.         } else if(opt == 3) {
  116.             int x = read(), z = read();
  117.             Add(1, 1, N, id[x], id[x] + siz[x] - 1, z);
  118.         } else if(opt == 4) {
  119.             int x = read();
  120.             cout << Query(1, 1, N, id[x] , id[x] + siz[x] - 1) << '\n';
  121.         }
  122.     }
  123.     return 0;
  124. }

树套树

  1. // luogu-judger-enable-o2
  2. // luogu-judger-enable-o2
  3. #include<iostream>
  4. #include<cstring>
  5. #include<cstdio>
  6. #include<algorithm>
  8. using namespace std;
  9. const int MAXN = 2000001;
  10. inline int read() {
  11.     char c = getchar();int x = 0,f = 1;
  12.     while(c < '0' || c > '9'){if(c == '-')f = -1;c = getchar();}
  13.     while(c >= '0' && c <= '9'){x = x * 10 + c - '0',c = getchar();}
  14.     return x * f;
  15. }
  16. #define Ls(k) s[k].ch[0]
  17. #define Rs(k) s[k].ch[1]
  18. struct sp {
  19.     int siz, ch[2], fa, rev, num;
  20. } s[MAXN];
  21. int sz;
  22. inline void pushup(int k) { //上传splay标记
  23.     s[k].siz = s[s[k].ch[0]].siz + s[s[k].ch[1]].siz + s[k].rev;
  24. }
  25. inline int ident(int x) { // 判断x是父亲的哪个儿子
  26.     return s[s[x].fa].ch[1] == x;
  27. }
  28. inline void connect(int x, int f, int how) {
  29.     s[x].fa = f; s[f].ch[how] = x;
  30. }
  31. inline void rotate(int &root,int x) { // 对x进行双旋操作
  32.     int Y = s[x].fa, R = s[Y].fa, Yson = ident(x), Rson = ident(Y);
  33.     int B = s[x].ch[Yson ^ 1];
  34.     if(!R) root = x;
  35.     connect(x, R, Rson);
  36.     connect(Y, x, Yson ^ 1);
  37.     connect(B, Y, Yson);
  38.     pushup(Y); pushup(x);
  39. }
  40. inline void splay(int &root, int x, int to) { // tag
  41.     while(s[x].fa != to) {
  42.         int y = s[x].fa;
  43.         if(s[y].fa == to) rotate(root, x);
  44.         else if(ident(x) == ident(y)) rotate(root, y),rotate(root, x);
  45.         else rotate(root, x),rotate(root, x);
  46.     }
  47. }
  48. inline void insert(int &k, int c) { // k节点，插入值为c的元素
  49.     if(k == 0) { 
  50.         k=++sz;
  51.         s[k].siz = s[k].rev = 1; s[k].num = c;
  52.         return ;
  53.     }
  54.     if(s[k].num==c) s[k].rev++;
  55.     else if(s[k].num < c) insert(Rs(k), c), s[Rs(k)].fa = k;
  56.     else insert(Ls(k), c), s[Ls(k)].fa = k;
  57.     pushup(k);
  58. }
  59. inline int getpre(int k,int val) { //小于val的最大值
  60.     int pos = k, ret;
  61.     while(pos) {
  62.         if(s[pos].num >= val) pos = Ls(pos);
  63.         else ret = pos, pos = Rs(pos);
  64.     }
  65.     return ret;
  66. }
  67. inline int getsuc(int k,int val) {
  68.     int pos = k, ret;
  69.     while(pos) {
  70.         if(s[pos].num <= val) pos = s[pos].ch[1];
  71.         else ret = pos, pos = s[pos].ch[0];
  72.     }
  73.     return ret;
  74. }
  75. inline int getk(int k,int val) {
  76.     if(s[k].num == val)   return k;
  77.     if(s[k].num < val)    return getk(Rs(k),val);
  78.     if(s[k].num > val)    return getk(Ls(k),val);
  79. }
  82. #define ls k << 1
  83. #define rs k << 1 | 1
  84. struct node {
  85.     int l, r, root, mx, mn;
  86. } T[MAXN];
  87. inline void pushup_s(int k) { // 上传线段树的标记
  88.     T[k].mx = max(T[ls].mx, T[rs].mx);
  89.     T[k].mn = min(T[ls].mn, T[rs].mn);
  90. }
  91. inline void Build(int k,int l,int r) { //下标为k，左端点为l，右端点为r
  92.     T[k].l = l; T[k].r = r;
  93.     if(l == r)    return ;
  94.     int mid = (l + r) >> 1;
  95.     Build(ls, l, mid);
  96.     Build(rs, mid + 1, r);// 线段树模板，没啥好说的，
  97. }
  98. inline void delet(int &k, int val) { //删除值为val的节点
  99.     int x = getk(k,val);//得到值为val的编号
  100.     if(s[x].rev > 1) { 
  101.         s[x].rev--; s[x].siz--;
  102.         splay(k, x, 0);
  103.     } else {
  104.         int p = getpre(k, val),su = getsuc(k, val);// 找到前驱和后继
  105.         splay(k, p, 0); splay(k, su, p);// 把前驱旋转到根节点，把后继旋转到根节点的孩子 
  106.         Ls(su) = 0;// 删除后继的左孩子，表示没有小于他的点，这样就成功把x节点删除 
  107.     }
  108. }
  109. inline void build(int k, int pos, int x) { // 在下标为k，位置为pos的地方插入一个值为x的元素 
  110.     insert(T[k].root, x);//在线段树root节点的splay中插入一个值为x的元素
  111.     if(T[k].l == T[k].r) {
  112.         T[k].mx = x; T[k].mn = x; 
  113.         return ;
  114.     }
  115.     int mid = (T[k].l + T[k].r) >> 1;
  116.     if(pos <= mid)  build(ls, pos, x);
  117.     if(pos > mid)   build(rs, pos, x);
  118.     pushup_s(k);//别忘了上传线段树标记 
  119. }
  120. int NewNode(int val, int f) {
  121.     s[++sz].rev = s[sz].siz = 1;
  122.     s[sz].num = val; s[sz].fa = f;
  123.     return sz;
  124. }
  125. inline void dfsseg(int k) { //对以k下标开始的线段树进行遍历
  126.     int x = getsuc(T[k].root, -1),
  127.         y = getpre(T[k].root, 1e8+1);//这样计算出来的x和y一定满足：x是k号线段树中的最小值的位置，y是k号线段树中最大值的位置
  128.     splay(T[k].root, x, 0);//将x旋转到根
  129.     s[x].siz++;
  130.     s[x].ch[0] = NewNode(-1, x);
  131.     splay(T[k].root, y, 0);
  132.     s[y].siz++;
  133.     s[y].ch[1] = NewNode(1e8 + 1, y);
  134.     if(T[k].l == T[k].r)    return ;
  135.     dfsseg(ls);
  136.     dfsseg(rs);// 对于每一个线段，增加两个虚节点
  137. }
  138. inline int getmax(int k,int l,int r) { //在l到r中找最大的元素
  139.     if(l <= T[k].l && T[k].r <= r) return T[k].mx;
  140.     int mid=(T[k].l + T[k].r) >> 1,ret = -1;
  141.     if(l <= mid)    ret = max(ret, getmax(ls, l, r));
  142.     if(mid <  r)    ret = max(ret, getmax(rs, l, r));
  143.     return ret;
  144. }
  145. inline int getmin(int k,int l,int r) { //在l到r中找最小的元素
  146.     if(l <= T[k].l && T[k].r <= r) return T[k].mn;
  147.     int mid = (T[k].l + T[k].r) >> 1,ret = 1e8+1;
  148.     if(l <= mid)    ret = min(ret, getmin(ls, l, r));
  149.     if(mid <  r)    ret = min(ret, getmin(rs, l, r));
  150.     return ret;
  151. }
  152. inline int query_order(int k, int l, int r, int val) { //下标为k，查询val在区间l到r中有多少比它小的数
  153.     if(l <= T[k].l && T[k].r <= r) {
  154.         int p = getpre(T[k].root, val);
  155.         splay(T[k].root, p, 0);
  156.         return s[p].siz - s[Rs(p)].siz - 1;//
  157.     } 
  158.     int mid = (T[k].l + T[k].r) >> 1, ret = 0;
  159.     if(l <= mid)    ret += query_order(ls, l, r, val);
  160.     if(r >  mid)    ret += query_order(rs, l, r, val);
  161.     return ret;
  162. }
  164. inline void modify(int k,int pos,int pre,int now) { //在下标为k的线段树中的pos位置值为pre的节点的值修改为now
  165.     delet(T[k].root, pre);// 先把pre删掉
  166.     insert(T[k].root, now);// 再把now加上
  167.     if(T[k].l==T[k].r) {
  168.         T[k].mx = now; T[k].mn = now; 
  169.         return ;
  170.     }
  171.     int mid = (T[k].l + T[k].r) >> 1;
  172.     if(pos <= mid)  modify(ls , pos, pre, now);
  173.     if(pos >  mid)  modify(rs , pos, pre, now);
  174.     pushup_s(k);// 别忘了上传标记！
  175. }
  176. inline int query_pre(int k,int l,int r,int val) {//查询区间l到r内val的前驱 
  177.     if(l <= T[k].l && T[k].r <= r) return s[getpre(T[k].root,val)].num;
  178.     int mid = (T[k].l + T[k].r) >> 1,ret = -1;
  179.     if(l <= mid)    ret = max(ret, query_pre(ls, l, r, val));
  180.     if(mid < r)     ret = max(ret, query_pre(rs, l, r, val));
  181.     return ret;
  182. }
  183. inline int query_suc(int k,int l,int r,int val) {//查询区间l到r内val的后继 
  184.     if(l <= T[k].l && T[k].r <= r) return s[getsuc(T[k].root,val)].num;
  185.     int mid = (T[k].l + T[k].r) >> 1, ret = 1e8 + 1;
  186.     if(l <= mid)    ret = min(ret, query_suc(ls, l, r, val));
  187.     if(mid <  r)    ret = min(ret, query_suc(rs, l, r, val));
  188.     return ret;
  189. }
  190. inline int QueryNum(int L,int R,int val) { // 在L到R的区间中查找val的排名
  191.     int l = 1, r = getmax(1, L, R), ret, tmp;
  192.     while(l <= r) { //二分答案
  193.         int mid = (l + r) >> 1;
  194.         tmp = query_order(1, L, R, mid);
  195.         if(tmp < val) ret = mid, l = mid + 1;
  196.         else r = mid - 1;
  197.     }
  198.     return ret;
  199. }
  200. int n, m;
  201. int date[MAXN];
  202. int main() {
  203. #ifdef WIN32
  204.     freopen("a.in", "r", stdin);
  205. #endif
  206.     n = read(); m = read();
  207.     Build(1, 1, n);//建好线段树
  208.     for(int i = 1; i <= n; i++) date[i] = read(); //读入初始数据
  209.     for(int i = 1; i <= n; i++)
  210.         build(1, i, date[i]);//把每一个元素都插到线段树里面去
  211.     dfsseg(1);// 把线段树的所有节点增加两个虚节点
  212.     while(m--) {
  213.         int l, r, k, pos, opt;
  214.         opt = read();
  215.         if(opt == 1) { //查询k在l到r中的排名
  216.             l = read(); r = read(); k = read();
  217.             printf("%d\n",query_order(1, l, r, k) + 1);
  218.         }
  219.         if(opt == 2) { // 查询排名为k的值
  220.             l = read(); r = read(); k = read();
  221.             printf("%d\n", QueryNum(l, r, k));
  222.         }
  223.         if(opt==3) { // 将pos位置的数修改为k
  224.             pos = read(); k = read();
  225.             modify(1, pos, date[pos], k);
  226.             date[pos] = k;//顺便修改date的值
  227.         }
  228.         if(opt==4) {
  229.             l = read(); r = read(); k = read();
  230.             int tmp = query_pre(1, l, r, k);// 查询tmp的前驱
  231.             if(tmp != -1) printf("%d\n", tmp);
  232.             else printf("-2147483647\n");
  233.         }
  234.         if(opt == 5) {
  235.             l = read(); r = read(); k = read();
  236.             int tmp = query_suc(1,l,r,k);
  237.             if(tmp != 1e8 + 1) printf("%d\n", tmp);
  238.             else printf("2147483647\n");
  239.         }
  240.     }
  241.     return 0;
  242. }

网络流

匈牙利算法

  1. #include<bits/stdc++.h>
  2. #define LL long long 
  3. using namespace std;
  4. const int MAXN = 1e3 + 10, INF = 1e9 + 10;
  5. inline int read() {
  6.     char c = getchar(); int x = 0, f = 1;
  7.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  8.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  9.     return x * f;
  10. }
  11. vector<int> v[MAXN];
  12. int N, M, E;
  13. int link[MAXN], vis[MAXN], cur = 1;
  14. int Aug(int x) {
  15.     for(int i = 0; i < v[x].size(); i++) {
  16.         int to = v[x][i];
  17.         if(vis[to] == cur) continue;
  18.         vis[to] = cur;
  19.         if(!link[to] || Aug(link[to])) {
  20.             link[to] = x;  
  21.             return 1;
  22.         }
  23.     }
  24.     return 0;
  25. }
  26. main() { 
  27. #ifdef WIN32
  28.     freopen("a.in", "r", stdin);
  29.     //freopen("b.out", "w", stdout);
  30. #endif
  31.     int N = read(), M = read(), E = read();
  32.     for(int i = 1; i <= E; i++) {
  33.         int x = read(), y = read();
  34.         if(x <= N && y <= M) {
  35.             v[x].push_back(y);      
  36.         }
  37.     }    
  38.     int ans = 0;
  39.     for(int i = 1; i <= N; i++, cur++)
  40.         if(Aug(i)) ans++;
  41.     printf("%d\n", ans);
  42.     return 0;
  43. }

Dinic

  1. #include<cstring>
  2. #include<cstdio>
  3. #define add_edge(x, y, z) AddEdge(x, y, z); AddEdge(y, x, 0);
  4. #define min(x, y) x < y ? x : y
  5. #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 19, stdin), p1 == p2) ? EOF : *p1++)
  6. #define rg register 
  7. const int MAXN = 10001, INF = 1e9 + 10;
  8. char buf[1 << 19], *p1 = buf, *p2 = buf;
  9. inline int read() {
  10.     char c = getchar(); int x = 0, f = 1;
  11.     while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();}
  12.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  13.     return x * f;
  14. }
  15. int N, M, S, T;
  16. struct node {
  17.     int u, v, f, nxt;
  18. }E[200002];
  19. int head[MAXN], cur[MAXN], num = 0, deep[MAXN], vis[MAXN], q[MAXN];
  20. inline void AddEdge(int x, int y, int z) {
  21.     E[num] = (node){x, y, z, head[x]};
  22.     head[x] = num++;
  23. }
  24. inline bool BFS() {
  25.     int l = 1, r = 1; q[r++] = S;
  26.     memset(deep, 0, sizeof(deep));
  27.     deep[S] = 1;
  28.     while(l < r) {
  29.         int p = q[l++];
  30.         for(rg int i = head[p]; i != -1; i = E[i].nxt) {
  31.             if(E[i].f && !deep[E[i].v]) {
  32.                 deep[E[i].v] = deep[p] + 1;
  33.                 if(E[i].v == T) return deep[T];
  34.                 q[r++] = E[i].v;
  35.             }
  36.         }
  37.     }
  38.     return deep[T];
  39. }
  40. int DFS(int x, int flow) {
  41.     if(x == T) return flow;
  42.     int ansflow = 0;
  43.     for(rg int &i = cur[x]; i != -1; i = E[i].nxt) {
  44.         if(deep[E[i].v] == deep[x] + 1 && E[i].f) {
  45.             int canflow = DFS(E[i].v, min(E[i].f, flow));
  46.             flow -= canflow;
  47.             E[i].f -= canflow; E[i ^ 1].f += canflow;
  48.             ansflow += canflow;
  49.             if(flow <= 0) break;
  50.         }
  51.     }
  52.     return ansflow;
  53. }
  54. inline int Dinic() {
  55.     int ans = 0;
  56.     while(BFS()) {
  57.         memcpy(cur, head, sizeof(head));
  58.         ans += DFS(S, INF);
  59.     }
  60.     return ans;
  61. }
  62. int main() {
  63.     #ifdef WIN32
  64.     freopen("a.in", "r", stdin);
  65.     #endif
  66.     memset(head, -1, sizeof(head));
  67.     N = read(); M = read(); S = read(); T = read();
  68.     for(rg int i = 1; i <= M; i++) {
  69.         rg int x = read(), y = read(), z = read();
  70.         add_edge(x, y, z);
  71.     }
  72.     printf("%d", Dinic());
  73.     return 0;
  74. }

最小费用最大流

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 1e5 + 10, INF = 1e9 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = 1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M, S, T;
  11. struct Edge {
  12.     int u, v, w, f, nxt;
  13. }E[MAXN];
  14. int head[MAXN], num = 0;
  15. inline void AddEdge(int x, int y, int w, int f) {
  16.     E[num] = (Edge){x, y, w, f, head[x]};
  17.     head[x] = num++;
  18. }
  19. int anscost, ansflow, dis[MAXN], vis[MAXN], Pre[MAXN];
  20. bool SPFA() {
  21.     memset(dis, 0x3f, sizeof(dis));
  22.     memset(vis, 0, sizeof(vis));
  23.     queue<int> q; q.push(S); dis[S] = 0;
  24.     while(!q.empty()) {
  25.         int p = q.front(); q.pop(); vis[p] = 0;
  26.         for(int i = head[p]; i !=- 1; i = E[i].nxt) {
  27.             int to = E[i].v;
  28.             if(dis[to] > dis[p] + E[i].w && E[i].f) {
  29.                 dis[to] = dis[p] + E[i].w;
  30.                 Pre[to] = i;
  31.                 if(!vis[to]) q.push(to), vis[to] = 1;
  32.             }
  33.         }
  34.     }
  35.     return dis[T] <= INF;
  36. }
  37. int F() {
  38.     int nowflow = INF;
  39.     for(int i = T; i != S; i = E[Pre[i]].u)
  40.         nowflow = min(nowflow, E[Pre[i]].f);
  41.     for(int i = T; i != S; i = E[Pre[i]].u)
  42.         E[Pre[i]].f -= nowflow, E[Pre[i] ^ 1].f += nowflow;
  43.     anscost += dis[T] * nowflow;
  44.     ansflow += nowflow; 
  45. }
  46. void MCMF() {
  47.     while(SPFA()) 
  48.         F();
  49. }
  50. int main() {
  51.     memset(head, -1, sizeof(head));
  52.     N = read(); M = read(); S = read(); T = read();
  53.     for(int i = 1; i <= M; i++) {
  54.         int x = read(), y = read(), f = read(), w = read();
  55.         AddEdge(x, y, w, f);
  56.         AddEdge(y, x, -w, 0);
  57.     }
  58.     MCMF();
  59.     printf("%d %d", ansflow, anscost);
  60.     return 0;
  61. }

图论

Dijkstra

  1. #include<cstdio>
  2. #include<algorithm>
  3. #include<cstring>
  4. #include<ext/pb_ds/priority_queue.hpp>
  5. #define MP(x, y) make_pair(x, y)
  6. #define Pair pair<int, int> 
  7. using namespace std;
  8. const int MAXN = 1e6 + 10, INF = 2147483646, B = 19;
  9. inline int read() {
  10.     char c = getchar(); int x = 0, f = 1;
  11.     while(c < '0' || c > '9') {if(c == '-') f = 1; c = getchar();}
  12.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  13.     return x * f;
  14. }
  15. int N, M, S;
  16. struct Edge {
  17.     int u, v, w, nxt;
  18. }E[MAXN];
  19. int head[MAXN], num = 1;
  20. void AddEdge(int x, int y, int z) {
  21.     E[num] = (Edge) {x, y, z, head[x]};
  22.     head[x] = num++;
  23. }
  24. int dis[MAXN], vis[MAXN];
  25. priority_queue<Pair> q; 
  26. void Dij() {
  27.     for(int i = 1; i <= N; i++) dis[i] = 2147483647;
  28.     dis[S] = 0; q.push(MP(0, S));
  29.     while(!q.empty()) {
  30.         int p = q.top().second; q.pop();
  31.         if(vis[p]) continue; vis[p] = 1;
  32.         for(int i = head[p]; i != -1; i = E[i].nxt) {
  33.             int to = E[i].v;
  34.             if(dis[to] > dis[p] + E[i].w) 
  35.                 dis[to] = dis[p] + E[i].w,
  36.                 q.push(MP(-dis[to], to));
  37.         }
  38.     }
  39.     for(int i = 1; i <= N; i++)
  40.         printf("%d ", dis[i]);
  41. }
  42. main() {
  43.     memset(head, -1, sizeof(head));
  44.     N = read(); M = read(); S = read();
  45.     for(int i = 1; i <= M; i++) {
  46.         int x = read(), y = read(), z = read();
  47.         AddEdge(x, y, z);
  48.     }
  49.     Dij();
  50.     return 0;
  51. }

Kruskal

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 1e6 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M;
  11. int fa[MAXN];
  12. struct Edge {
  13.     int u, v, w;
  14.     bool operator < (const Edge &rhs) const {
  15.         return w < rhs.w;
  16.     }
  17. }E[MAXN];
  18. int find(int x) {
  19.     return fa[x] == x ? fa[x] : fa[x] = find(fa[x]);
  20. }
  21. int unionn(int x, int y) {
  22.     x = find(x); y = find(y);
  23.     fa[x] = y;
  24. }
  25. int main() {
  26.     N = read(); M = read();
  27.     for(int i = 1; i <= N; i++) fa[i] = i;
  28.     for(int i = 1; i <= M; i++) {
  29.         int x = read(), y = read(), z = read();
  30.         E[i] = (Edge) {x, y, z};
  31.     }
  32.     sort(E + 1, E + M + 1);
  33.     int ans = 0;
  34.     for(int i = 1; i <= M; i++) {
  35.         int x = E[i].u, y = E[i].v;
  36.         if(find(x) == find(y)) continue;
  37.         ans += E[i].w;
  38.         unionn(x, y);
  39.     }
  40.     cout << ans;
  41.     return 0;
  42. }

tarjan

缩点

  1. #include<bits/stdc++.h>
  2. #define LL long long 
  3. using namespace std;
  4. const int MAXN = 2e6 + 10, mod = 998244353;
  5. inline int read() {
  6.     char c = getchar(); int x = 0, f = 1;
  7.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  8.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  9.     return x * f;
  10. }
  12. int N, M, a[MAXN];
  13. struct Edge {
  14.     int u, v, nxt;
  15. }E[MAXN];
  16. int head[MAXN], num = 1;
  17. inline void AE(int x, int y) {
  18.     E[num] = (Edge) {x, y, head[x]};
  19.     head[x] = num++;
  20. }
  21. vector<int> v[MAXN];
  22. int dfn[MAXN], low[MAXN], vis[MAXN], tim, st[MAXN], col[MAXN], top, cn, inter[MAXN];
  23. int sum[MAXN], f[MAXN];
  24. void tarjan(int x) {
  25.     dfn[x] = low[x] = ++tim;
  26.     vis[x] = 1; 
  27.     st[++top] = x;
  28.     for(int i = head[x]; ~i; i = E[i].nxt) {
  29.         int to = E[i].v;
  30.         if(!dfn[to]) tarjan(to), low[x] = min(low[to], low[x]);
  31.         else if(vis[to]) low[x] = min(low[to], low[x]);
  32.     }
  33.     if(dfn[x] == low[x]) {
  34.         int h; cn++;
  35.         do {
  36.             h = st[top--];
  37.             col[h] = cn; sum[cn] += a[h]; vis[h] = 0;
  38.         }while(h != x);
  39.     }
  40. }
  41. void Topsort() {
  42.     queue<int> q;
  43.     for(int i = 1; i <= cn; i++) if(!inter[i]) q.push(i), f[i] = sum[i];
  44.     int ans = 0;
  45.     while(!q.empty()) {
  46.         int p = q.front(); q.pop();
  47.         ans = max(ans, f[p]);
  48.         for(auto to: v[p]) {
  49.             inter[to]--;
  50.             f[to] = max(f[to], f[p] + sum[to]);
  51.             if(!inter[to]) q.push(to);
  52.         }
  53.     }
  54.     cout << ans << '\n';
  55. }
  56. signed main() {   
  57. #ifndef ONLINE_JUDGE
  58.      freopen("a.in", "r", stdin); freopen("a.out", "w", stdout);
  59. #endif 
  60.     memset(head, -1, sizeof(head));
  61.     N = read(); M = read();
  62.     for(int i = 1; i <= N; i++) a[i] = read();
  63.     for(int i = 1; i <= M; i++) {
  64.         int x = read(), y = read();
  65.         AE(x, y);
  66.     }
  67.     for(int i = 1; i <= N; i++) if(!dfn[i]) tarjan(i);
  68.     for(int i = 1; i <= N; i++) {
  69.         for(int j = head[i]; ~j; j = E[j].nxt) {
  70.             int to = E[j].v;
  71.             if(col[i] != col[to]) {
  72.                 v[col[i]].push_back(col[to]);
  73.                 inter[col[to]]++;
  74.             }
  75.         }
  76.     }
  77.     Topsort();
  78.     return 0;
  79. }

割点

给出一个n个点，m条边的无向图，求图的割点。

  1. // luogu-judger-enable-o2
  2. // luogu-judger-enable-o2
  3. #include<bits/stdc++.h>
  4. #define Pair pair<int, int>
  5. #define MP make_pair 
  6. #define fi first
  7. #define se second 
  8. using namespace std;
  9. const int MAXN = 2e5 + 10;
  10. inline int read() {
  11.     char c = getchar(); int x = 0, f = 1;
  12.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  13.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  14.     return x * f;
  15. }
  16. int N, M, dfn[MAXN], low[MAXN], tot, cut[MAXN];
  17. vector<int> v[MAXN];
  18. void tarjan(int x, int fa) {
  19.     dfn[x] = low[x] = ++tot; int ch = 0;
  20.     for(int i = 0; i < v[x].size(); i++) {
  21.         int to = v[x][i];
  22.         if(!dfn[to]) {
  23.             tarjan(to, x), low[x] = min(low[x], low[to]), ch++;
  24.             if(low[to] >= dfn[x] && (x != fa)) cut[x] = 1;
  25.         }
  26.         low[x] = min(low[x], dfn[to]);
  28.     }
  29.     if(x == fa && ch > 1) cut[x] = 1;
  30. }
  31. int main() {    
  32.     N = read(); M = read();
  33.     for(int i = 1; i <= M; i++) {
  34.         int x = read(), y = read();
  35.         v[x].push_back(y); v[y].push_back(x);
  36.     }
  37.     for(int i = 1; i <= N; i++) if(!dfn[i]) tarjan(i, i);
  38.     int tot = 0;
  39.     for(int i = 1; i <= N; i++) if(cut[i]) tot++;
  40.     printf("%d\n", tot);
  41.     for(int i = 1; i <= N; i++) if(cut[i]) printf("%d ", i);
  42.     return 0;
  43. }

割边

  1. #include<cstdio>
  2. #include<cstring>
  3. #include<algorithm>
  4. #include<stack>
  5. //#define getchar() (S == T && (T = (S = BB) + fread(BB, 1, 1 << 15, stdin), S == T) ? EOF : *S++)
  6. //char BB[1 << 15], *S = BB, *T = BB;
  7. using namespace std;
  8. const int MAXN=1e5+10;
  9. inline int read()
  10. {
  11.     char c=getchar();int x=0,f=1;
  12.     while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
  13.     while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
  14.     return x*f;
  15. }
  16. struct node
  17. {
  18.     int u,v,nxt;
  19. }edge[MAXN];
  20. int head[MAXN],num=1;
  21. inline void AddEdge(int x,int y)
  22. {
  23.     edge[num].u=x;
  24.     edge[num].v=y;
  25.     edge[num].nxt=head[x];
  26.     head[x]=num++;
  27. }
  28. int N,M;
  29. int angry[1001][1001];
  30. int dfn[MAXN],low[MAXN],tot=0,point[MAXN],color[MAXN],in[MAXN],ans[MAXN];
  31. stack<int>s;
  32. void pre()
  33. {
  34.     memset(angry,0,sizeof(angry));
  35.     num=1;
  36.     memset(head,-1,sizeof(head));
  37.     memset(ans,0,sizeof(ans));
  38.     memset(dfn,0,sizeof(dfn));
  39.     memset(low,0,sizeof(low));
  40. }
  41. bool MakeColor(int now,int how)
  42. {
  43.     color[now]=how;
  44.     for(int i=head[now];i!=-1;i=edge[i].nxt)
  45.     {
  46.         if(!in[edge[i].v]) continue;
  47.         if(!color[edge[i].v]&&!MakeColor(edge[i].v,how^1)) return 0;
  48.         else if(color[edge[i].v]==color[now]) return 0;
  49.     }
  50.     return 1;
  51. }
  52. void tarjan(int now,int fa)
  53. {
  54.     dfn[now]=low[now]=++tot;
  55.     s.push(now);
  56.     for(int i=head[now];i!=-1;i=edge[i].nxt)
  57.     {
  58.         if(!dfn[edge[i].v]&&edge[i].v!=fa)
  59.         {
  60.             tarjan(edge[i].v,now);
  61.             low[now]=min(low[now],low[edge[i].v]);
  62.             if(low[edge[i].v]>=dfn[now])
  63.             {
  64.                 memset(in,0,sizeof(in));//哪些在双联通分量里
  65.                 memset(color,0,sizeof(color));
  66.                 int h=0,cnt=0;
  67.                 do
  68.                 {
  69.                     h=s.top();s.pop();
  70.                     in[h]=1;
  71.                     point[++cnt]=h;
  72.                 }while(h!=edge[i].v);//warning 
  73.                 if(cnt<=1) continue;//必须构成环 
  74.                 in[now]=1;point[++cnt]=now;
  75.                 if(MakeColor(now,1)==0)
  76.                     for(int j=1;j<=cnt;j++)
  77.                         ans[point[j]]=1;
  78.             }
  79.         }
  80.         if(edge[i].v!=fa) low[now]=min(low[now],dfn[edge[i].v]);
  81.     }
  82. }
  83. int main()
  84. {
  85.     #ifdef WIN32
  86.     freopen("a.in","r",stdin);
  87.     #else
  88.     #endif
  89.     while(scanf("%d%d",&N,&M))
  90.     {
  91.         if(N==0&&M==0) break;
  92.         pre();
  93.         for(int i=1;i<=M;i++)
  94.         {
  95.             int x=read(),y=read();
  96.             angry[x][y]=angry[y][x]=1;
  97.         }
  98.         for(int i=1;i<=N;i++)
  99.             for(int j=1;j<=N;j++)
  100.                 if(i!=j&&(!angry[i][j]))
  101.                     AddEdge(i,j);
  102.         for(int i=1;i<=N;i++)
  103.             if(!dfn[i])
  104.                 tarjan(i,0);
  105.         int out=0;
  106.         for(int i=1;i<=N;i++)
  107.             if(!ans[i]) out++;
  108.         printf("%d\n",out);
  109.     }
  110.     return 0;
  111. }

字符串

后缀数组

对于一个字符串，求每次插入一个字符之后得到的本质不同的子串数

  1. #include<bits/stdc++.h>
  2. #define sit set<int>::iterator
  3. #define LL long long 
  4. using namespace std;
  5. const int MAXN = 2e5 + 10;
  6. const int INF = 2333;
  7. inline int read() {
  8.     char c = getchar(); int x = 0, f = 1;
  9.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  10.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  11.     return x * f;
  12. }
  13. int N, M, L, rak[MAXN], tax[MAXN], tp[MAXN], sa[MAXN], H[MAXN], f[MAXN][20], lg2[MAXN], s[MAXN], date[MAXN], ans[MAXN];
  14. set<int> st;
  15. void Qsort() {
  16.     for(int i = 0; i <= M; i++) tax[i] = 0;
  17.     for(int i = 1; i <= N; i++) tax[rak[i]]++;
  18.     for(int i = 1; i <= M; i++) tax[i] += tax[i - 1];
  19.     for(int i = N; i >= 1; i--) sa[tax[rak[tp[i]]]--] = tp[i];
  20. }
  21. void SuffixSort() {
  22.     for(int i = 1; i <= N; i++) rak[i] = s[i], tp[i] = i; M = 233; Qsort();
  23.     for(int w = 1, p = 0; p < N; w <<= 1, M = p) { p = 0;
  24.         for(int i = 1; i <= w; i++) tp[++p] = N - i + 1;
  25.         for(int i = 1; i <= N; i++) if(sa[i] > w) tp[++p] = sa[i] - w;
  26.         Qsort(); swap(tp, rak); rak[sa[1]] = p = 1;
  27.         for(int i = 2; i <= N; i++) rak[sa[i]] = (tp[sa[i]] == tp[sa[i - 1]] && tp[sa[i] + w] == tp[sa[i - 1] + w]) ? p : ++p;
  28.     }
  29.     for(int i = 1, k = 0; i <= N; i++) {
  30.         if(k) k--; int j = sa[rak[i] - 1];
  31.         while(s[i + k] == s[j + k]) k++;
  32.         H[rak[i]] = k;
  33.     } 
  34. }
  35. void Pre() {
  36.     for(int i = 1; i <= N; i++) f[i][0] = H[i];
  37.     for(int j = 1; j <= 17; j++)
  38.         for(int i = 1; i + (1 << j) - 1 <= N; i++) f[i][j] = min(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
  39. }
  40. int Query(int x, int y) {
  41.     if(x > y) swap(x, y); x++;
  42.     int k = lg2[y - x + 1];
  43.     return min(f[x][k], f[y - (1 << k) + 1][k]);
  44. }
  45. void Des() {
  46.     sort(date + 1, date + N + 1);
  47.     int num = unique(date + 1, date + N + 1) - date - 1;
  48.     for(int i = 1; i <= N; i++) s[i] = lower_bound(date + 1, date + num + 1, s[i]) - date;
  49.     reverse(s + 1, s + N + 1);
  50. }
  51. int main() {
  52.     lg2[1] = 0; for(int i = 2; i <= MAXN - 1; i++) lg2[i] = lg2[i >> 1] + 1;
  53.     N = read();
  54.     for(int i = 1; i <= N; i++) s[i] = date[i] = read();
  55.     Des();  
  56.     SuffixSort(); Pre();
  57.     st.insert(0); st.insert(N + 1);
  58.     LL now = 0; st.insert(rak[N]); ans[N] = 1;
  59.     printf("%lld\n", 1);
  60.     for(int i = N - 1; i >= 1; i--) {
  61.         sit nxt = st.upper_bound(rak[i]), pre;
  62.         if(*nxt == 0) pre = st.begin();
  63.         else pre = --nxt, nxt++;
  64.     //  printf("%d %d\n", *pre, *nxt);
  65.         if(*pre != 0 && *nxt != N + 1) now -= Query(*pre, *nxt);
  66.         if(*pre != 0 && *pre != N + 1) now += Query(*pre, rak[i]);
  67.         if(*nxt != 0 && *nxt != N + 1) now += Query(rak[i], *nxt);
  68.         printf("%lld\n", 1ll * (N - i + 1) * ((N - i + 1) + 1) / 2 - now);
  69.         st.insert(rak[i]);
  70.     }
  71.     return 0;
  72. }

后缀自动机

题目同上

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 4e5 + 10;
  4. int N, fa[MAXN], len[MAXN], las = 1, tot = 1, root = 1;
  5. long long sum;
  6. map<int, int> ch[MAXN];
  7. long long Insert(int x) {
  8.     int now = ++tot, pre = las; las = now; len[now] = len[pre] + 1;
  9.     for(; pre && !ch[pre][x]; pre = fa[pre]) ch[pre][x] = now;
  10.     if(!pre) fa[now] = root;
  11.     else {
  12.         int q = ch[pre][x];
  13.         if(len[pre] + 1 == len[q]) fa[now] = q;
  14.         else {
  15.             int nq = ++tot; fa[nq] = fa[q]; len[nq] = len[pre] + 1;
  16.             ch[nq] = ch[q];
  17.             for(; pre && ch[pre][x] == q; pre = fa[pre]) ch[pre][x] = nq;
  18.             fa[now] = fa[q] = nq;
  19.         }
  20.     }
  21.     return sum += len[now] - len[fa[now]];
  22. }
  23. int main() {
  24.     cin >> N;
  25.     for(int i = 1; i <= N; i++) {
  26.         int x; cin >> x;
  27.         cout << Insert(x) << '\n';
  28.     }
  29.     return 0;
  30. }

回文自动机

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 1e6 + 10;
  4. char s[MAXN];
  5. int len[MAXN], N, num[MAXN], fail[MAXN], last, cur, pos, trie[MAXN][26], tot = 1; 
  6. int getfail(int x, int i) {
  7.     while(i - len[x] - 1 < 0 || s[i - len[x] - 1] != s[i]) x = fail[x];
  8.     return x;
  9. }
  11. int main() {
  12.     scanf("%s", s);
  13.     N = strlen(s);
  14.     fail[0] = 1; len[1] = -1;
  15.     for(int i = 0; i <= N - 1; i++) {
  16.         if(i >= 1) s[i] = (s[i] + last - 97) % 26 + 97;
  17.         pos = getfail(cur, i);
  18.         if(!trie[pos][s[i] - 'a']) {
  19.             fail[++tot] = trie[getfail(fail[pos], i)][s[i] - 'a'];
  20.             trie[pos][s[i] - 'a'] = tot;
  21.             len[tot] = len[pos] + 2;
  22.             num[tot] = num[fail[tot]] + 1;  
  23.         }
  24.         cur = trie[pos][s[i] - 'a'];
  25.         last = num[cur];
  26.         printf("%d ", last);
  27.     }
  28.     return 0;
  29. }

AC自动机

有 N 个由小写字母组成的模式串以及一个文本串 T。每个模式串可能会在文本串中出现多次。你需要找出哪些模式串在文本串 T 中出现的次数最多。

  1. #include<cstdio>
  2. #include<cstring>
  3. #include<queue>
  4. #include<vector>
  5. using namespace std;
  6. const int MAXN = 1e6 + 10, B = 26;
  7. int T; 
  8. char s[201][75], a[MAXN];
  9. int N; 
  10. int fail[MAXN], ch[MAXN][27], val[MAXN], root = 0, tot = 0, sum[MAXN];
  11. void insert(char *s, int I) {
  12.     int N = strlen(s + 1);
  13.     int now = root;
  14.     for(int i = 1; i <= N; i++) {
  15.         int x = s[i] - 'a';
  16.         if(!ch[now][x]) ch[now][x] = ++tot;
  17.         now = ch[now][x];
  18.     }
  19.     val[now] = I;
  20. }
  21. void GetFail() {
  22.     queue<int> q;
  23.     for(int i = 0; i < B; i++) if(ch[root][i]) q.push(ch[root][i]);
  24.     while(!q.empty()) {
  25.         int p = q.front(); q.pop();
  26.         for(int i = 0; i < B; i++) 
  27.             if(ch[p][i]) fail[ch[p][i]] = ch[fail[p]][i], q.push(ch[p][i]);
  28.             else ch[p][i] = ch[fail[p]][i];
  29.     }
  30. }
  31. int main() {
  32.     while(scanf("%d", &T) && T) {
  33.         memset(fail, 0, sizeof(fail)); memset(ch, 0, sizeof(ch)); 
  34.         memset(val, 0, sizeof(val)); memset(fail, 0, sizeof(fail));
  35.         memset(sum, 0, sizeof(sum)); memset(s, 0, sizeof(s));
  36.         for(int i = 1; i <= T; i++) scanf("%s", s[i] + 1), insert(s[i], i);
  37.         GetFail();
  38.         scanf("%s", a + 1);
  39.         int N = strlen(a + 1), now = root;
  40.         for(int i = 1; i <= N; i++) {
  41.             now = ch[now][a[i] - 'a'];
  42.             for(int t = now; t; t = fail[t]) if(val[t]) sum[val[t]]++;
  43.         }
  44.         int ans = 0;
  45.         for(int i = 1; i <= T; i++) ans = max(ans, sum[i]);
  46.         printf("%d\n", ans);
  47.         for(int i = 1; i <= T; i++)
  48.             if(sum[i] == ans)
  49.                 printf("%s\n", s[i] + 1);
  50.     } 
  51.     return 0;
  52. }

可持久化trie树

给定一个非负整数序列{a}，初始长度为N。
有M个操作，有以下两种操作类型：
1、Ax：添加操作，表示在序列末尾添加一个数x，序列的长度N+1。
2、Qlrx：询问操作，你需要找到一个位置p，满足l<=p<=r，使得：
a[p] xor a[p+1] xor ... xor a[N] xor x 最大，输出最大是多少。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 6e5 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-')f =- 1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M, a[MAXN], sum[MAXN], cnt[MAXN * 25], ch[MAXN * 25][2], tot, root[MAXN];
  11. void insert(int i, int x) {
  12.     x = (sum[i] = sum[i - 1] ^ x);
  13.     int p = root[i - 1], now = (root[i] = ++tot);
  14.     for(int i = 23; i >= 0; i--) {
  15.         bool nxt = x >> i & 1;
  16.         ch[now][nxt ^ 1] = ch[p][nxt ^ 1];
  17.         now = ch[now][nxt] = ++tot; p = ch[p][nxt];
  18.         cnt[now] = cnt[p] + 1;
  19.     }
  20. }
  21. int Query(int l, int r, int x) {
  22.     r = root[r], l = root[l];
  23.     int ans = 0;
  24.     for(int i = 23; i >= 0; i--) {
  25.         int nxt = x >> i & 1;
  26.         if(cnt[ch[r][nxt ^ 1]] - cnt[ch[l][nxt ^ 1]] > 0) ans += 1 << i, r = ch[r][nxt ^ 1], l = ch[l][nxt ^ 1];
  27.         else r = ch[r][nxt], l = ch[l][nxt];
  28.     }
  29.     return ans;
  30. }
  31. int main() {
  32.     N = read(); M = read();
  33.     for(int i = 1; i <= N; i++) a[i] = read(), insert(i, a[i]);
  34.     char ss[4];
  35.     for(int i = 1; i <= M; i++) {
  36.         scanf("%s", ss + 1);
  37.         if(ss[1] == 'A') 
  38.             N++, a[N] = read(), insert(N, a[N]);
  39.         else {
  40.             int l = read() - 1, r = read() - 1, val = read();
  41.             printf("%d\n", Query(l - 1, r, val ^ sum[N]));
  42.         }
  43.     }
  44. }

KMP

  1. #include<bits/stdc++.h> 
  2. #define Pair pair<int, int>
  3. #define MP(x, y) make_pair(x, y)
  4. #define fi first
  5. #define se second
  6. #define LL long long 
  7. #define ull unsigned long long 
  8. #define Fin(x) {freopen(#x".in","r",stdin);}
  9. #define Fout(x) {freopen(#x".out","w",stdout);}
  10. #define pb push_back 
  11. using namespace std;
  12. const int MAXN = 1e6 + 10, mod = 1e9 + 7, INF = 1e9 + 10;
  13. const double eps = 1e-9;
  14. inline int read() {
  15.     char c = getchar(); int x = 0, f = 1;
  16.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  17.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  18.     return x * f;
  19. }
  20. int N, M, P[MAXN];
  21. char s1[MAXN], s2[MAXN];
  22. void GetFail() {
  23.     int j = 0;
  24.     for(int i = 2; i <= N; i++) {
  25.         while(j && s2[i] != s2[j + 1]) j = P[j];
  26.         if(s2[j + 1] == s2[i]) P[i] = ++j;
  27.     }
  28. }
  29. void KMP() {
  30.     int j = 0;
  31.     for(int i = 1; i <= N; i++) {
  32.         while(j && s1[i] != s2[j + 1]) j = P[j];
  33.         if(s1[i] == s2[j + 1]) j++;
  34.         if(j == M) 
  35.             cout << (i - j + 1) << '\n';
  36.     }
  37. }
  38. signed main() {
  39.     scanf("%s", s1 + 1);
  40.     scanf("%s", s2 + 1);
  41.     N = strlen(s1 + 1); M = strlen(s2 + 1);
  42.     GetFail();
  43.     KMP();
  44.     for(int i = 1; i <= M; i++) cout << P[i] << ' ';
  45. }

manacher

求字符串中回文串的最长长度

  1. // luogu-judger-enable-o2
  2. #include<bits/stdc++.h> 
  3. #define Pair pair<int, int>
  4. #define MP(x, y) make_pair(x, y)
  5. #define fi first
  6. #define se second
  7. #define LL long long 
  8. using namespace std;
  9. const int MAXN = 11000000 * 2 + 1, mod = 1e9 + 7, INF = 1e9 + 10;
  10. const double eps = 1e-9;
  11. inline int read() {
  12.     char c = getchar(); int x = 0, f = 1;
  13.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  14.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  15.     return x * f;
  16. }
  17. int ch(int x, int l, int r) {
  18.     return x >= l && x <= r;
  19. }
  20. char s[MAXN];
  21. int N, ans[MAXN];
  22. void trans() {
  23.     static char tmp[MAXN];
  24.     tmp[0] = '#';
  25.     for(int i = 1; i <= N; i++) {
  26.         tmp[2 * i - 1] = s[i];
  27.         tmp[2 * i] = '#';
  28.     }
  29.     memcpy(s, tmp, sizeof(s));
  30.     N = (N << 1) - 1;
  31.     int mx = 0, id = 0;
  32.     for(int i = 1; i <= N; i++) {
  33.         ans[i] = (mx > i ? min(mx - i, ans[id * 2 - i]) : 1);
  34.         while(i >= ans[i] && s[i - ans[i]] == s[i + ans[i]]) 
  35.             ans[i]++;
  36.         if(i + ans[i] > mx) mx = i + ans[i], id = i;
  37.     }
  38. }
  39. signed main() {
  40.     scanf("%s", s + 1);
  41.     N = strlen(s + 1);
  42.     trans();
  43.     int out = 0;
  44.     for(int i = 1; i <= N; i++) chmax(out, ans[i]);
  45.     cout << out - 1;
  46.     return 0;
  47. }

数学

线性代数

矩阵求逆

  1. #include<bits/stdc++.h> 
  2. #define LL long long 
  3. using namespace std;
  4. const int MAXN = 2001, mod = 1e9 + 7;
  5. const double eps = 1e-9;
  6. inline int read() {
  7.     char c = getchar(); int x = 0, f = 1;
  8.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  9.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  10.     return x * f;
  11. }
  12. int N, a[MAXN][MAXN];
  13. int mul(int x, int y) {
  14.     return 1ll * x * y % mod;
  15. }
  16. int fp(int a, int p) {
  17.     int base = 1;
  18.     while(p) {
  19.         if(p & 1) base = mul(base, a);
  20.         a = mul(a, a); p >>= 1;
  21.     }
  22.     return base;
  23. }
  24. int inv(int x) {
  25.     return fp(x, mod - 2);
  26. }
  27. void add2(int &x, int y) {
  28.     if(x + y < 0) x = x + y + mod;
  29.     else x = (x + y >= mod) ? x + y - mod : x + y;
  30. }
  31. int MatrixInv() {
  32.     for(int i = 1; i <= N; i++) 
  33.         a[i][i + N] = 1;
  34.     for(int i = 1; i <= N; i++) {
  35.         int mx = i;
  36.         for(int j = i + 1; j <= N; j++)
  37.             if(a[j][i] > a[i][i]) mx = j;
  38.         if(mx != i) swap(a[i], a[mx]);
  39.         if(!a[i][i]) return -1; 
  40.         int Inv = inv(a[i][i]);
  41.         for(int j = i; j <= 2 * N; j++) a[i][j] = mul(a[i][j], Inv);
  42.         for(int j = 1; j <= N; j++) {
  43.             if(i != j) {
  44.                 int r = a[j][i];
  45.                 for(int k = i; k <= 2 * N; k++) 
  46.                     add2(a[j][k], -mul(a[i][k], r));                
  47.             }
  48.         }
  49.     }   
  50.     return 0;
  51. }
  52. signed main() {
  53.     //freopen("testdata.in", "r", stdin);
  54.     N = read();
  55.     for(int i = 1; i <= N; i++)
  56.         for(int j = 1; j <= N; j++) 
  57.             a[i][j] = read();
  58.     if(MatrixInv() == -1) {puts("No Solution"); return 0;}
  59.     for(int i = 1; i <= N; i++, puts(""))
  60.         for(int j = N + 1; j <= 2 * N; j++)
  61.             printf("%d ", a[i][j]);
  62.     return 0;
  63. }

动态规划及其优化

虚树

国家有一个大工程，要给一个非常大的交通网络里建一些新的通道。

我们这个国家位置非常特殊，可以看成是一个单位边权的树，城市位于顶点上。

在 2 个国家 a,b 之间建一条新通道需要的代价为树上 a,b 的最短路径。

现在国家有很多个计划，每个计划都是这样，我们选中了 k 个点，然后在它们两两之间 新建 C(k,2)条 新通道。现在对于每个计划，我们想知道： 1.这些新通道的代价和 2.这些新通道中代价最小的是多少 3.这些新通道中代价最大的是多少

  1. #include<bits/stdc++.h> 
  2. #define Pair pair<int, int>
  3. #define MP(x, y) make_pair(x, y)
  4. #define fi first
  5. #define se second
  6. #define int long long 
  7. #define LL long long 
  8. #define Fin(x) {freopen(#x".in","r",stdin);}
  9. #define Fout(x) {freopen(#x".out","w",stdout);}
  10. using namespace std;
  11. const int MAXN = 2e6 + 10, mod = 1e9 + 7, INF = 1e9 + 10;
  12. const double eps = 1e-9;
  13. template <typename A, typename B> inline bool chmin(A &a, B b){if(a > b) {a = b; return 1;} return 0;}
  14. template <typename A, typename B> inline bool chmax(A &a, B b){if(a < b) {a = b; return 1;} return 0;}
  15. template <typename A, typename B> inline LL add(A x, B y) {if(x + y < 0) return x + y + mod; return x + y >= mod ? x + y - mod : x + y;}
  16. template <typename A, typename B> inline void add2(A &x, B y) {if(x + y < 0) x = x + y + mod; else x = (x + y >= mod ? x + y - mod : x + y);}
  17. template <typename A, typename B> inline LL mul(A x, B y) {return 1ll * x * y % mod;}
  18. template <typename A, typename B> inline void mul2(A &x, B y) {x = (1ll * x * y % mod + mod) % mod;}
  19. template <typename A> inline void debug(A a){cout << a << '\n';}
  20. template <typename A> inline LL sqr(A x){return 1ll * x * x;}
  21. inline int read() {
  22.     char c = getchar(); int x = 0, f = 1;
  23.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  24.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  25.     return x * f;
  26. }
  27. int N, dfn[MAXN];
  28. vector<int> v[MAXN], E[MAXN];
  29. namespace HLP {
  30.     int fa[MAXN], siz[MAXN], son[MAXN], dep[MAXN], top[MAXN], times;
  31.     void dfs1(int x, int _fa) {
  32.         siz[x] = 1; fa[x] = _fa; dep[x] = dep[_fa] + 1; dfn[x] = ++times;
  33.         for(auto &to : v[x]) {
  34.             if(to == _fa) continue;
  35.             dfs1(to, x);
  36.             siz[x] += siz[to];
  37.             if(siz[to] > siz[son[x]]) son[x] = to;
  38.         }
  39.     }
  40.     void dfs2(int x, int topf) {
  41.         top[x] = topf; 
  42.         if(!son[x]) return ;
  43.         dfs2(son[x], topf);
  44.         for(auto &to : v[x]) {
  45.             if(top[to]) continue;
  46.             dfs2(to, to);
  47.         }
  48.     }
  49.     int LCA(int x, int y) {
  50.         while(top[x] ^ top[y]) {
  51.             if(dep[top[x]] < dep[top[y]]) swap(x, y);
  52.             x = fa[top[x]];
  53.         }
  54.         return dep[x] < dep[y] ? x : y;
  55.     }       
  56. }   
  57. int p[MAXN], st[MAXN], top, f[MAXN], mx[MAXN], mn[MAXN], siz2[MAXN], d[MAXN], ans1, ans2, ans3;
  58. void AE(int x, int y) {E[x].push_back(y);}
  59. int comp(int a, int b) {return dfn[a] < dfn[b];}
  60. int dis(int x, int y) {if(dfn[x] > dfn[y]) swap(x, y); return HLP::dep[y] - HLP::dep[x];}
  61. queue<int> q;
  62. void insert(int x) {
  63.     if(top == 1) {st[++top] = x; return ;}
  64.     int lca = HLP::LCA(x, st[top]);
  65.     if(lca == st[top]) {st[++top] = x; return ;}
  66.     while(top > 1 && dfn[st[top - 1]] >= dfn[lca]) AE(st[top - 1], st[top]), top--;
  67.     if(lca != st[top]) 
  68.         AE(lca, st[top]), st[top] = lca;
  69.     st[++top] = x;
  70. }
  71. //ans1 和 ans2最大值 ans3最小值
  72. void DP(int x) {
  73.     q.push(x);
  74.     mn[x] = (siz2[x] ? 0 : 1e18);
  75.     mx[x] = 0; d[x] = 0;
  76.     for(auto &to : E[x]) {
  77.         int w = dis(x, to);
  78.         assert(w <= N);
  79.         DP(to);
  80.         if(siz2[x] > 0) {
  81.             ans1 += w * siz2[to] * siz2[x] + siz2[to] * d[x] + siz2[x] * d[to];
  82.             chmax(ans2, mx[x] + mx[to] + w);
  83.             chmin(ans3, mn[x] + mn[to] + w);
  84.         }
  85.         chmax(mx[x], w + mx[to]);
  86.         chmin(mn[x], w + mn[to]);
  87.         siz2[x] += siz2[to]; 
  88.         d[x] += d[to] + w * siz2[to];
  89.     }
  90.     E[x].clear();
  91. }
  92. void work() {   
  93.     ans1 = ans2 = 0; ans3 = INF;
  94.     int K = read(); st[top = 1] = 1;
  95.     for(int i = 1; i <= K; i++) p[i] = read();
  96.     sort(p + 1, p + K + 1, comp);
  97.     for(int i = 1; i <= K; i++) {
  98.         if(p[i] != 1) insert(p[i]);
  99.         siz2[p[i]] = 1;
  100.     }
  101.     while(top > 1) AE(st[top - 1], st[top]), top--;
  102.     DP(1);
  103.     while(!q.empty()) siz2[q.front()] = 0, q.pop();
  104.     cout << ans1 << ' ' << ans3 << ' ' << ans2 << '\n';
  105. }
  106. signed main() {
  107.     N = read();
  108.     for(int i = 1; i <= N - 1; i++) {
  109.         int x = read(), y = read();
  110.         v[x].push_back(y);
  111.         v[y].push_back(x);
  112.     }
  113.     HLP::dfs1(1, 0); HLP::dfs2(1, 1);
  114.     int Q = read(); 
  115.     while(Q--) {
  116.         work();
  117.     }
  118.     return 0;
  119. }

动态dp

  1. #include<bits/stdc++.h>
  2. #define LL long long 
  3. using namespace std;
  4. const int MAXN = 1e5 + 10, INF = INT_MAX;
  5. template<typename A, typename B> inline bool chmax(A &x, B y) {
  6.     return x < y ? x = y, 1 : 0;
  7. }
  8. inline int read() {
  9.     char c = getchar(); int x = 0, f = 1;
  10.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  11.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  12.     return x * f;
  13. }
  14. int N, M, a[MAXN], f[MAXN][2];
  15. struct Ma {
  16.     LL m[3][3];
  17.     Ma() {
  18.         memset(m, -0x3f, sizeof(m));
  19.     }
  20.     Ma operator * (const Ma &rhs) const {
  21.         Ma ans;
  22.         for(int i = 1; i <= 2; i++)
  23.             for(int j = 1; j <= 2; j++)
  24.                 for(int k = 1; k <= 2; k++)
  25.                     chmax(ans.m[i][j], m[i][k] + rhs.m[k][j]);
  26.         return ans;
  27.     }
  28. }val[MAXN], sum[MAXN];
  29. vector<int> v[MAXN];
  30. int ch[MAXN][2], fa[MAXN];
  31. #define ls(x) ch[x][0]
  32. #define rs(x) ch[x][1]
  33. void update(int k) {
  34.     sum[k] = val[k];
  35.     if(rs(k)) sum[k] = sum[k] * sum[rs(k)];
  36.     if(ls(k)) sum[k] = sum[ls(k)] * sum[k];
  37. }
  38. bool ident(int x) {
  39.     return rs(fa[x]) == x;
  40. }
  41. bool isroot(int x) {
  42.     return ls(fa[x]) != x && rs(fa[x]) != x;
  43. }
  44. void connect(int x, int _fa, int tag) {
  45.     fa[x] = _fa;
  46.     ch[_fa][tag] = x;
  47. }
  48. void rotate(int x) {
  49.     int y = fa[x], r = fa[y], yson = ident(x), rson = ident(y);
  50.     int b = ch[x][yson ^ 1];
  51.     fa[x] = r;
  52.     if(!isroot(y)) connect(x, r, rson);
  53.     connect(b, y, yson);
  54.     connect(y, x, yson ^ 1);
  55.     update(y); update(x);
  56. }
  57. void splay(int x) {
  58.     for(int y = fa[x]; !isroot(x); rotate(x), y = fa[x])
  59.         if(!isroot(y))
  60.             rotate(ident(y) == ident(x) ? y : x);
  61. }
  62. void access(int x) {
  63.     for(int y = 0; x; x = fa[y = x]) {
  64.         splay(x);
  65.         if(rs(x)) {
  66.             val[x].m[1][1] += max(sum[rs(x)].m[1][1], sum[rs(x)].m[2][1]);
  67.             val[x].m[2][1] += sum[rs(x)].m[1][1];
  68.         }
  69.         if(y) {
  70.             val[x].m[1][1] -= max(sum[y].m[1][1], sum[y].m[2][1]);
  71.             val[x].m[2][1] -= sum[y].m[1][1];
  72.         }
  73.         val[x].m[1][2] = val[x].m[1][1];
  74.         rs(x) = y;
  75.         update(x);
  76.     }
  77. }
  78. int Modify(int p, int v) {
  79.     access(p); splay(p);
  80.     val[p].m[2][1] -= a[p] - v; 
  81.     update(p);
  82.     a[p] = v;
  83.     splay(1);
  84.     return max(sum[1].m[1][1], sum[1].m[2][1]);
  85. }
  86. void dfs(int x, int _fa) {
  87.     fa[x] = _fa;
  88.     f[x][1] = a[x];
  89.     for(auto &to : v[x]) {
  90.         if(to == _fa) continue;
  91.         dfs(to, x);
  92.         f[x][0] += max(f[to][0], f[to][1]);
  93.         f[x][1] += f[to][0];
  94.     }
  95.     val[x].m[1][1] = f[x][0]; val[x].m[1][2] = f[x][0];
  96.     val[x].m[2][1] = f[x][1]; val[x].m[2][2] = -INF;
  97.     update(x);
  98. //  sum[x] = val[x];
  99. }
  100. int main() {
  101.     //freopen("a.in", "r", stdin);
  102.     N = read(); M = read();
  103.     for(int i = 1; i <= N; i++) a[i] = read();
  104.     for(int i = 1; i < N; i++) {
  105.         int x = read(), y = read();
  106.         v[x].push_back(y);
  107.         v[y].push_back(x);
  108.     }
  109.     dfs(1, 0);
  110.     while(M--) {
  111.         int x = read(), y = read();
  112.         printf("%d\n", Modify(x, y));
  113.     }
  114.     return 0;
  115. }

斜率优化cdq

  1. #include<bits/stdc++.h> 
  2. #define Pair pair<double, double>
  3. #define MP(x, y) make_pair(x, y)
  4. #define fi first
  5. #define se second
  6. #define int long long 
  7. #define LL long long 
  8. #define db  double
  9. #define Fin(x) {freopen(#x".in","r",stdin);}
  10. #define Fout(x) {freopen(#x".out","w",stdout);}
  11. using namespace std;
  12. const int MAXN = 1e6 + 10, mod = 1e9 + 7, INF = 1e18 + 10;
  13. const double eps = 1e-9;
  14. template <typename A, typename B> inline bool chmin(A &a, B b){if(a > b) {a = b; return 1;} return 0;}
  15. template <typename A, typename B> inline bool chmax(A &a, B b){if(a < b) {a = b; return 1;} return 0;}
  16. template <typename A, typename B> inline LL add(A x, B y) {if(x + y < 0) return x + y + mod; return x + y >= mod ? x + y - mod : x + y;}
  17. template <typename A, typename B> inline void add2(A &x, B y) {if(x + y < 0) x = x + y + mod; else x = (x + y >= mod ? x + y - mod : x + y);}
  18. template <typename A, typename B> inline LL mul(A x, B y) {return 1ll * x * y % mod;}
  19. template <typename A, typename B> inline void mul2(A &x, B y) {x = (1ll * x * y % mod + mod) % mod;}
  20. template <typename A> inline void debug(A a){cout << a << '\n';}
  21. template <typename A> inline LL sqr(A x){return 1ll * x * x;}
  22. inline int read() {
  23.     char c = getchar(); int x = 0, f = 1;
  24.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  25.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  26.     return x * f;
  27. }
  28. int N;
  29. struct Sta {
  30.     int id;
  31.     db h, w, x, y, f, ad;
  32.     void Get() {
  33.         x = 2 * h;
  34.         y = f + h * h - w;
  35.     }
  36. }a[MAXN], st[MAXN];
  37. vector<Pair> v;
  38. int comp(const Sta &a, const Sta &b) {
  39.     return a.id < b.id;
  40. }
  41. double GetK(Pair a, Pair b) {
  42.     if((b.fi - a.fi) < eps) return INF;
  43.     return (b.se - a.se) / (b.fi - a.fi);
  44. }
  46. int sid[MAXN], cur;
  48. void GetConvexHull(int l, int r) {
  49.     while(cur) sid[cur--] = 0;
  50.     v.clear();
  51.     for(int i = l; i <= r; i++) {
  52.         double x = a[i].x, y = a[i].y;
  53.         while((v.size() > 1 && ((GetK(v[v.size() - 1], MP(x, y)) < GetK(v[v.size() - 2], v[v.size() - 1])))) ||
  54.               ((v.size() > 0) && (v[v.size() - 1].fi == x) && (v[v.size() - 1].se >= y))) 
  55.             v.pop_back(), sid[cur--] = 0;
  56.         v.push_back(MP(x, y));  sid[++cur] = a[i].id;
  57.     }
  58. }
  59. int cnt = 0;
  60. db Find(int id, db k) {
  61.     int tmp = v.size();
  62.     int l = 0, r = v.size() - 1, ans = 0;
  63.     while(l <= r) {
  64.         int mid = l + r >> 1;
  65.         if((mid == v.size() - 1) || (GetK(v[mid], v[mid + 1]) > k)) r = mid - 1, ans = mid;
  66.         else l = mid + 1;
  67.     }
  68.     return v[ans].se - k * v[ans].fi;
  69. }
  70. void CDQ(int l, int r) {
  71.     if(l == r) {
  72.         a[l].Get(); 
  73.         return ;   
  74.     }
  75.     int mid = l + r >> 1;
  76.     CDQ(l, mid); 
  77.     GetConvexHull(l, mid);
  78.     for(int i = mid + 1; i <= r; i++) {
  79.         chmin(a[i].f, Find(i, a[i].h) + a[i].ad);
  80.     }
  81.     CDQ(mid + 1, r);
  82.     int tl = l, tr = mid + 1, tot = tl - 1;
  83.     while(tl <= mid || tr <= r) {
  84.         if((tr > r) || (tl <= mid && a[tl].x < a[tr].x)) st[++tot] = a[tl++];//?????tl <= mid 
  85.         else st[++tot] = a[tr++];
  86.     }
  87.     for(int i = l; i <= r; i++) a[i] = st[i]; 
  88. }
  89. signed main() {
  90.     N = read(); 
  91.     for(int i = 1; i <= N; i++) a[i].h = read();
  92.     for(int i = 1; i <= N; i++) {
  93.         a[i].w = read() + a[i - 1].w; a[i].id = i;
  94.         a[i].f = a[i - 1].f + sqr(a[i].h - a[i - 1].h);
  95.         a[i].ad = sqr(a[i].h) + a[i - 1].w;
  96.         if(i == 1) a[1].f = 0;
  97.     }
  98.     CDQ(1, N);
  99.     sort(a + 1, a + N + 1, comp);
  100. //  for(int i = 1; i <= N; i++) cout << i << ' ' << (LL)a[i].f << '\n';
  101.     cout << (LL)a[N].f;
  102.     return 0;
  103. }

斜率优化队列

  1. // luogu-judger-enable-o2
  2. #include<bits/stdc++.h> 
  3. #define Pair pair<int, int>
  4. #define MP(x, y) make_pair(x, y)
  5. #define fi first
  6. #define se second
  7. #define int long long 
  8. #define LL long long 
  9. #define Fin(x) {freopen(#x".in","r",stdin);}
  10. #define Fout(x) {freopen(#x".out","w",stdout);}
  11. using namespace std;
  12. const int MAXN = 1e6 + 10, mod = 1e9 + 7;
  13. LL INF = 2e18 + 10;
  14. const double eps = 1e-9;
  15. template <typename A, typename B> inline bool chmin(A &a, B b){if(a > b) {a = b; return 1;} return 0;}
  16. template <typename A, typename B> inline bool chmax(A &a, B b){if(a < b) {a = b; return 1;} return 0;}
  17. template <typename A, typename B> inline LL add(A x, B y) {if(x + y < 0) return x + y + mod; return x + y >= mod ? x + y - mod : x + y;}
  18. template <typename A, typename B> inline void add2(A &x, B y) {if(x + y < 0) x = x + y + mod; else x = (x + y >= mod ? x + y - mod : x + y);}
  19. template <typename A, typename B> inline LL mul(A x, B y) {return 1ll * x * y % mod;}
  20. template <typename A, typename B> inline void mul2(A &x, B y) {x = (1ll * x * y % mod + mod) % mod;}
  21. template <typename A> inline void debug(A a){cout << a << '\n';}
  22. template <typename A> inline LL sqr(A x){return 1ll * x * x;}
  23. inline int read() {
  24.     char c = getchar(); int x = 0, f = 1;
  25.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  26.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  27.     return x * f;
  28. }
  29. int N, w[MAXN], d[MAXN], s[MAXN], sw[MAXN], g[MAXN], f[MAXN], q[MAXN];
  30. int calc(int l, int r) {
  31.     if(l > r) return 0; 
  32.     return s[r] - s[l - 1] - d[l - 1] * (sw[r] - sw[l - 1]);
  33. }
  34. double Y(int x) {
  35.     return g[x];
  36. }
  37. double X(int x) {
  38.     return d[x];
  39. }
  40. double slope(int a, int b) {
  41.     return double(Y(b) - Y(a)) / (X(b) - X(a));
  42. }
  43. signed main() {
  44.     N = read();
  45.     for(int i = 1; i <= N; i++) w[i] = read(), d[i] = read();
  46.     reverse(w + 1, w + N + 1); reverse(d + 1, d + N + 1);
  47.     for(int i = 1; i <= N; i++) d[i] += d[i - 1], s[i] = s[i - 1] + w[i] * d[i], sw[i] = w[i] + sw[i - 1];
  48.     LL ans = INF;
  49.     for(int i = 1; i <= N; i++) g[i] = calc(1, i - 1)- s[i] + d[i] * sw[i];
  50.     q[1] = 0; 
  51.     for(int i = 1, h = 1, t = 1; i <= N; i++) {
  52.         f[i] = INF; 
  53.         while(h < t && slope(q[h], q[h + 1]) < sw[i - 1]) h++;
  54.         f[i] = g[q[h]] - d[q[h]] * sw[i - 1];
  55.         while(h < t && slope(q[t - 1], q[t]) > slope(q[t], i)) t--;
  56.         q[++t] = i;
  57.         //for(int j = i - 1; j >= 1; j--) chmin(f[i], g[j] - d[j] * sw[i - 1]);
  59.         f[i] += s[i - 1];
  60.     }
  61.     for(int i = 1; i <= N; i++) 
  62.         f[i] += calc(i + 1, N), chmin(ans, f[i]);
  63.     cout << ans;
  64.     return 0;
  65. }

矩阵快速幂

  1. #include<bits/stdc++.h>
  2. #define LL long long 
  3. using namespace std;
  4. const int MAXN = 2e7 + 10, mod = 20170408, SS = 1e5 + 10;
  5. LL GG = 1e17;
  6. inline int read() {
  7.     char c = getchar(); int x = 0, f = 1;
  8.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  9.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  10.     return x * f;
  11. }
  12. template<typename A, typename B> inline int add(A x, B y) {
  13.     if(x + y < 0) return x + y + mod;
  14.     else return x + y >= mod ? x + y - mod : x + y;
  15. }
  16. template<typename A, typename B> inline void add2(A &x, B y) {
  17.     if(x + y < 0) x = x + y + mod;
  18.     else x = (x + y >= mod ? x + y - mod : x + y);
  19. }
  20. template<typename A, typename B> inline int mul(A x, B y) {
  21.     return 1ll * x * y % mod;
  22. }
  23. int N, M, p, Lim;//1 - M, ºÍÊÇpµÄ±¶Êý 
  24. int f[SS], vis[MAXN], mu[MAXN], prime[MAXN], tot, cnt, num[SS], tim[SS], val[SS];
  25. struct Ma {
  26.     int m[201][201];
  27.     Ma() {
  28.         memset(m, 0, sizeof(m));
  29.     }
  30.     void init() {
  31.         for(int i = 0; i <= Lim; i++) m[i][i] = 1;
  32.     }
  33.     void clear() {
  34.         memset(m, 0, sizeof(m));
  35.     }
  36.     void print() {
  37.         for(int i = 0; i <= Lim; i++, puts(""))
  38.             for(int j = 0; j <= Lim; j++)
  39.                 printf("%d ", m[i][j]);
  40.     }
  41.     Ma operator * (const Ma &rhs) const {
  42.         Ma ans = {};
  43.         for(int i = 0; i <= Lim; i++)
  44.             for(int j = 0; j <= Lim; j++) {
  45.                 __int128 tmp = 0;
  46.                 for(int k = 0; k <= Lim; k++) {
  47.                     tmp += 1ll * m[i][k] * rhs.m[k][j];     
  48.                 }
  49.                 ans.m[i][j] = tmp % mod;
  50.             }
  51.         return ans;
  52.     }
  53. }g;
  54. Ma MatrixPow(Ma a, int p) {
  55.     Ma base; base.init();
  56.     while(p) {
  57.         if(p & 1) base = base * a;
  58.         a = a * a; p >>= 1;
  59.     }
  60.     return base;
  61. }
  62. void sieve(int N) {
  63.     vis[1] = 1; mu[1] = 1; 
  64.     for(int i = 2; i <= N; i++) {
  65.         if(!vis[i]) prime[++tot] = i, mu[i] = -1;
  66.         for(int j = 1; j <= tot && i * prime[j] <= N; j++) {
  67.             vis[i * prime[j]] = 1;
  68.             if(i % prime[j]) mu[i * prime[j]] = -mu[i];
  69.             else {mu[i * prime[j]] = 0; break;}
  70.         }
  71.     }
  72.     for(int i = 1; i <= N; i++) 
  73.         if(vis[i]) num[i % p]++;
  74. }
  76. int solve1() {//ºöÊÓÖÊÊýµÄÏÞÖÆ
  77.     for(int i = 1; i <= M; i++) f[i % p]++;
  78.     for(int j = 0; j < p; j++) {
  79.         memset(tim, 0, sizeof(tim));
  80.         memset(val, 0, sizeof(val));
  81.         int step = M;
  82.         for(int k = 1; k <= M; k++) {
  83.             int nxt = (j + k) % p;
  84.             if(tim[nxt]) {step = k - 1; break;}
  85.             tim[nxt] = 1; val[nxt]++;
  86.         }
  87.         if(step) for(int k = 0; k <= Lim; k++) g.m[k][j] = M / step * val[k];
  88.         for(int k = M / step * step + 1; k <= M; k++) g.m[(j + k) % p][j]++;
  89.     }
  90.     Ma ans = MatrixPow(g, N - 1);
  91.     int out = 0;
  92.     for(int i = 0; i <= Lim; i++) add2(out, mul(ans.m[0][i], f[i]));
  93.     return out;
  94. }
  95. int solve2() {//ÎÞÖÊÊý 
  96.     memset(f, 0, sizeof(f));
  97.     g.clear();
  98.     for(int i = 1; i <= M; i++) f[i % p] += (vis[i]);
  99.     for(int j = 0; j < p; j++)
  100.         for(int k = 0; k < p; k++)
  101.             g.m[(j + k) % p][j] += num[k];
  103.     Ma ans = MatrixPow(g, N - 1);
  104.     int out = 0;
  105.     for(int i = 0; i <= Lim; i++) 
  106.         add2(out, mul(ans.m[0][i], f[i]));
  107.     return out;
  108. }
  109. int main() {
  110.     N = read(); M = read(); Lim = p = read();
  111.     sieve(M);
  112.     cout << (solve1() - solve2() + mod) % mod;
  113.     return 0;
  114. }

分块

莫队

一个长为 n 的序列 a。
有 m 个询问，每次询问三个区间，把三个区间中同时出现的数一个一个删掉，问最后三个区间剩下的数的个数和，询问独立。
注意这里删掉指的是一个一个删，不是把等于这个值的数直接删完，
比如三个区间是 [1,2,2,3,3,3,3] , [1,2,2,3,3,3,3] 与 [1,1,2,3,3]，就一起扔掉了 1 个 1，1 个 2，2 个 3。

  1. #include<cstdio>
  2. #include<algorithm>
  3. #include<cstring>
  4. #include<iostream>
  5. #include<cmath>
  6. #include<bitset>
  7. #define LL long long
  8. // #define int long long  
  9. using namespace std;
  10. const int MAXN = 1e5 + 10, B = 25000;
  11. inline int read() {
  12.     char c = getchar(); int x = 0, f = 1;
  13.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  14.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  15.     return x * f;
  16. }
  17. int N, M;
  18. int a[MAXN], date[MAXN], L[MAXN][5], R[MAXN][5], belong[MAXN], base, cnt = 0, flag[MAXN], tim[MAXN], ans[MAXN];
  19. struct Query {
  20.     int l, r, opt, id;
  21.     bool operator < (const Query &rhs) const {
  22.         return belong[l] == belong[rhs.l] ? belong[r] < belong[rhs.r] : belong[l] < belong[rhs.l];
  23.     }
  24. }Q[MAXN * 3 + 1];
  25. bitset<MAXN> bit[B + 50], now;
  26. void Add(int x) {
  27.     tim[a[x]]++; 
  28.     now.set(a[x] + tim[a[x]] - 1);
  29. }
  30. void Delet(int x) {
  31.     now.reset(a[x] + tim[a[x]] - 1);
  32.     tim[a[x]]--;
  33. }
  34. void solve(int ll, int rr) {
  35.     memset(flag, 0, sizeof(flag));
  36.     memset(tim, 0, sizeof(tim));
  37.     memset(ans, 0, sizeof(ans));
  38.     now.reset();
  39.     for(int i = 0; i <= B; i++) bit[i].reset();
  40.     cnt = 0;
  41.     for(int ti = ll; ti <= rr; ti++) {
  42.         for(int i = 1; i <= 3; i++) 
  43.             Q[++cnt] = (Query){L[ti][i], R[ti][i], i, ti - ll + 1},
  44.             ans[ti - ll + 1] += (R[ti][i] - L[ti][i] + 1);
  45.     }
  46.     sort(Q + 1, Q + cnt + 1);
  47.     int l = 1, r = 0;
  48.     for(int i = 1; i <= cnt; i++) {    
  49.         while(l > Q[i].l) Add(--l);
  50.         while(r < Q[i].r) Add(++r);
  51.         while(l < Q[i].l) Delet(l++);
  52.         while(r > Q[i].r) Delet(r--);
  53.         if(!flag[Q[i].id]) 
  54.             bit[Q[i].id] = now, flag[Q[i].id] = 1; 
  55.         else 
  56.             bit[Q[i].id] &= now;
  57.     }
  58.    // sort(Q + 1, Q + cnt + 1, comp);
  59.     for(int i = ll; i <= rr; i++)
  60.         printf("%d\n", ans[i - ll + 1] - bit[i - ll + 1].count() * 3);
  61. }
  62. main() {
  63. ///    freopen("xp1.in", "r", stdin);
  64. //    freopen("ans.out", "w", stdout);
  65.     N = read(); M = read(); base = sqrt(N);
  66.     for(int i = 1; i <= N; i++) a[i] = read(), date[i] = a[i], belong[i] = (i - 1) / base + 1;
  67.     sort(date + 1, date + N + 1);
  68.     for(int i = 1; i <= N; i++) a[i] = lower_bound(date + 1, date + N + 1, a[i]) - date;
  69.     for(int i = 1; i <= M; i++) {
  70.         //L1[i] = read(); R1[i] = read(); L2[i] = read(); R2[i] = read(); L3[i] = read(); R3[i] = read();
  71.         for(int j = 1; j <= 3; j++) L[i][j] = read(), R[i][j] = read();
  72.     }
  73.     for(int i = 1; i <= N; i += B + 1) 
  74.         solve(i, min(i + B, M));
  76.     return 0;
  77. }
  78. /*
  79. */

回滚莫队

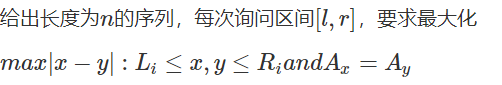
  1. #include<bits/stdc++.h>
  3. const int MAXN = 1e5 + 10, INF = 1e9 + 7;
  4. using namespace std;
  5. template<typename A, typename B> inline bool chmax(A &x, B y) {
  6.     if(y > x) {x = y; return 1;}
  7.     else return 0;
  8. }
  9. template<typename A, typename B> inline bool chmin(A &x, B y) {
  10.     if(y < x) {x = y; return 1;}
  11.     else return 0;
  12. }
  13. inline int read() {
  14.     char c = getchar(); int x = 0, f = 1;
  15.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  16.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  17.     return x * f;
  18. }
  19. int N, K, M, a[MAXN], l[MAXN], r[MAXN], tl[MAXN], tr[MAXN], belong[MAXN], block, cnt, ans[MAXN];
  20. struct query {
  21.     int l, r, id;
  22.     bool operator < (const query &rhs) const {
  23.         return belong[l] == belong[rhs.l] ? r < rhs.r : belong[l] < belong[rhs.l];
  24.     }
  25. };
  26. vector<query> q[MAXN];
  27. int solve(int l, int r) {
  28.     for(int i = l; i <= r; i++) tl[a[i]] = INF, tr[a[i]] = 0;
  29.     int ans = 0;
  30.     for(int i = l; i <= r; i++) {
  31.         int x = a[i];
  32.         chmin(tl[x], i), chmax(tr[x], i);
  33.         chmax(ans, tr[x] - tl[x]);
  34.     }
  35.     return ans;
  36. }
  37. int update(int x) {
  38.     chmax(tr[a[x]], x);
  39.     chmin(tl[a[x]], x);
  40.     return tr[a[x]] - tl[a[x]];
  41. }
  42. int update2(int x) {
  43.     int v = a[x];
  44.     chmax(r[v], x);
  45.     chmin(l[v], x);
  46.     return max(tr[v] - l[v], r[v] - l[v]);
  47. }
  48. void LxlDuLiu(vector<query> v, int id) {
  49.     int base = id * block, ll = base, rr = ll - 1, pre = 0, now = 0;
  50.     memset(tr, 0, sizeof(tr)); memset(r, 0, sizeof(r));
  51.     memset(tl, 0x3f, sizeof(tl)); memset(l, 0x3f, sizeof(l));
  53.     for(auto &x : v) {
  54.         //memset(l, 0x3f, sizeof(l)); memset(r, 0, sizeof(r));
  55.         while(rr < x.r) chmax(now, update(++rr));
  56.         pre = now;
  57.         while(ll > x.l) chmax(now, update2(--ll));
  58.         chmax(ans[x.id], now);
  59.         while(ll < base) r[a[ll]] = 0, l[a[ll]] = INF, ll++;
  60.         now = pre;
  61.     }
  62. }
  63. int main() {
  64. //  freopen("a.in", "r", stdin);
  65.     //freopen("b.out", "w", stdout);
  67.     N = read(); K = read(); M = read(); block = sqrt(N); int mx = 0;
  68.     for(int i = 1; i <= N; i++) a[i] = read(), belong[i] = (i - 1) / block + 1, chmax(mx, belong[i]);
  69.     for(int i = 1; i <= M; i++) {
  70.         int l = read(), r = read();
  71.         if(belong[l] == belong[r]) ans[i] = solve(l, r);
  72.         else q[belong[l]].push_back({l, r, i});
  73.     }
  74.     for(int i = 1; i <= mx; i++) sort(q[i].begin(), q[i].end());
  75.     for(int i = 1; i <= mx; i++)
  76.         LxlDuLiu(q[i], i);
  77.     for(int i = 1; i <= M; i++) printf("%d\n", ans[i]);
  79.     return 0;
  80. }

带修改莫队

  1. // luogu-judger-enable-o2
  2. // luogu-judger-enable-o2
  3. #include<cstdio>
  4. #include<cmath>
  5. #include<algorithm>
  6. #define swap(x, y) x ^= y, y ^= x, x^= y
  7. using namespace std;
  8. const int MAXN= 2*1e6+10;
  9. inline int read() {
  10.     char c=getchar();int x=0,f=1;
  11.     while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
  12.     while(c>='0'&&c<='9'){x=x*10+c-'0',c=getchar();}
  13.     return x*f;
  14. }
  15. char obuf[1<<24], *O=obuf;
  16. void print(int x) {
  17.     if(x > 9) print(x / 10);
  18.     *O++ = x % 10 + '0';
  19. }
  20. int N, M;
  21. int a[MAXN], where[MAXN];
  22. struct Query {
  23.     int x, y, pre, id;
  24. }Q[MAXN];
  25. int Qnum = 0;
  26. struct Change {
  27.     int pos,val;
  28. }C[MAXN];
  29. int Cnum = 0;
  30. int color[MAXN], ans=0, base, out[MAXN];
  31. int comp(const Query &a,const Query &b) {
  32.     return where[a.x] == where[b.x] ? ( where[a.y] == where[b.y] ? a.pre < b.pre : a.y < b.y ): a.x < b.x ;
  33. }
  34. void Add(int val){if(++color[val]==1) ans++; } 
  35. void Delet(int val){ if(--color[val]==0) ans--; }
  36. void Work(int now, int i) {
  37.     if(C[now].pos >= Q[i].x && C[now].pos <= Q[i].y) {
  38.         if( --color[a[C[now].pos]] == 0 ) ans--;
  39.         if( ++color[C[now].val] == 1)     ans++; 
  40.     }
  41.     swap(C[now].val, a[C[now].pos]);
  42. }
  43. void MoQueue()
  44. {
  45.     int l = 1, r = 0, now = 0; 
  46.     for(int i = 1;i <= Qnum;i++)
  47.     {
  48.         while(l < Q[i].x) Delet(a[l++]);
  49.         while(l > Q[i].x) Add(a[--l]);
  50.         while(r < Q[i].y) Add(a[++r]);
  51.         while(r > Q[i].y) Delet(a[r--]); 
  52.         while(now < Q[i].pre) Work(++now, i);
  53.         while(now > Q[i].pre) Work(now--, i);
  54.         out[Q[i].id] = ans;
  55.     }
  56.     for(int i = 1;i <= Qnum; i++)
  57.         print(out[i]), *O++ = '\n';
  58. }
  59. int main()
  60. {
  61.     #ifdef WIN32
  62.     freopen("a.in", "r", stdin);
  63.     freopen("a.out","w",stdout); 
  64.     #endif
  65.     N = read();M = read();
  66.     for(int i = 1;i <= N; i++) a[i] = read();
  67.     while(M--)
  68.     {
  69.         char opt[5];
  70.         scanf("%s",opt);
  71.         if(opt[0] == 'Q') {
  72.             Q[++Qnum].x = read();
  73.             Q[Qnum].y = read();
  74.             Q[Qnum].pre = Cnum;//???????????? 
  75.             Q[Qnum].id = Qnum;        
  76.         }
  77.         else if(opt[0] == 'R') {
  78.             C[++Cnum].pos = read();
  79.             C[Cnum].val = read();
  80.         }
  81.     }
  82.     base = pow(N, 0.6666666666);
  83.     for(int i = 1; i <= N; i++) where[i] = i / base + 1;
  84.     sort(Q+1, Q+Qnum+1, comp);
  85.     MoQueue();
  86.     fwrite(obuf, O-obuf, 1, stdout);
  87.     return 0;
  88. }

树上莫队

给定一个n个节点的树，每个节点表示一个整数，问u到v的路径上有多少个不同的整数。

  1. #include<cstdio>
  2. #include<cmath>
  3. #include<algorithm>
  4. #include<vector>
  5. //#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
  6. char buf[1 << 21], *p1 = buf, *p2 = buf;
  7. using namespace std;
  8. const int MAXN = 1e5 + 10;
  9. inline int read() {
  10.     char c = getchar(); int x = 0, f = 1;
  11.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  12.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  13.     return x * f;
  14. }
  15. int N, Q;
  16. int belong[MAXN], block;
  17. struct Query {
  18.     int l, r, ID, lca, ans;
  19.     bool operator < (const Query &rhs) const{
  20.         return belong[l] == belong[rhs.l] ? r < rhs.r : belong[l] < belong[rhs.l];
  21.     //    return belong[l] < belong[rhs.l];
  22.     }
  23. }q[MAXN];
  24. vector<int>v[MAXN];
  25. int a[MAXN], date[MAXN];
  26. void Discretization() {
  27.     sort(date + 1, date + N + 1);
  28.     int num = unique(date + 1, date + N + 1) - date - 1;
  29.     for(int i = 1; i <= N; i++) a[i] = lower_bound(date + 1, date + num + 1, a[i]) - date;    
  30. }
  31. int deep[MAXN], top[MAXN], fa[MAXN], siz[MAXN], son[MAXN], st[MAXN], ed[MAXN], pot[MAXN], tot;
  32. void dfs1(int x, int _fa) {
  33.     fa[x] = _fa; siz[x] = 1;
  34.     st[x] = ++ tot; pot[tot] = x; 
  35.     for(int i = 0; i < v[x].size(); i++) {
  36.         int to = v[x][i];
  37.         if(deep[to]) continue;
  38.         deep[to] = deep[x] + 1;
  39.         dfs1(to, x);
  40.         siz[x] += siz[to];
  41.         if(siz[to] > siz[son[x]]) son[x] = to;
  42.     }
  43.     ed[x] = ++tot; pot[tot] = x;
  44. }
  45. void dfs2(int x, int topfa) {
  46.     top[x] = topfa;
  47.     if(!son[x]) return ;
  48.     dfs2(son[x], topfa);
  49.     for(int i = 0; i < v[x].size(); i++) {
  50.         int to = v[x][i];
  51.         if(top[to]) continue;
  52.             dfs2(to, to);
  53.     }
  54. }
  55. int GetLca(int x, int y) {
  56.     while(top[x] != top[y]) {
  57.         if(deep[top[x]] < deep[top[y]]) swap(x, y);
  58.         x = fa[top[x]];
  59.     }
  60.     return deep[x] < deep[y] ? x : y;
  61. }
  62. void DealAsk() {
  63.     for(int i = 1; i <= Q; i++) {
  64.         int x = read(), y = read();
  65.         if(st[x] > st[y]) swap(x, y);
  66.         int _lca = GetLca(x, y);
  67.         q[i].ID = i;
  68.         if(_lca == x) q[i].l = st[x], q[i]. r = st[y];
  69.         else q[i].l = ed[x], q[i].r = st[y], q[i].lca = _lca;
  70.     }
  71. }
  72. int Ans, out[MAXN], used[MAXN], happen[MAXN];
  73. void add(int x) {
  74.     if(++happen[x] == 1) Ans++;
  75. }
  76. void delet(int x) {
  77.     if(--happen[x] == 0) Ans--;
  78. }
  79. void Add(int x) {
  80.     used[x] ? delet(a[x]) : add(a[x]); used[x] ^= 1;
  81. }
  82. void Mo() {
  83.     sort(q + 1, q + Q + 1);
  84.     int l = 1, r = 0, fuck = 0;
  85.     for(int i = 1; i <= Q; i++) {
  86.         while(l < q[i].l) Add(pot[l]), l++, fuck++;
  87.         while(l > q[i].l) l--, Add(pot[l]), fuck++;
  88.         while(r < q[i].r) r++, Add(pot[r]), fuck++;
  89.         while(r > q[i].r) Add(pot[r]), r--, fuck++;
  90.         if(q[i].lca) Add(q[i].lca);
  91.         q[i].ans = Ans;
  92.         if(q[i].lca) Add(q[i].lca);
  93.     }
  94.     for(int i = 1; i <= Q; i++) out[q[i].ID] = q[i].ans;
  95.     for(int i = 1; i <= Q; i++)
  96.         printf("%d\n", out[i]);
  97. }
  98. int main() {
  99.     N = read(); Q = read();
  100.     //block = 1.5 * sqrt(2 * N) + 1;
  101.     //block = pow(N, 0.66666666666);
  102.     block = sqrt(N);
  103.     for(int i = 1; i <= N; i++) a[i] = date[i] = read();
  104.     for(int i = 1; i <= N * 2; i++) belong[i] = i / block + 1;
  105.     Discretization();
  106.     for(int i = 1; i <= N - 1; i++) {
  107.         int x = read(), y = read();
  108.         v[x].push_back(y); v[y].push_back(x);
  109.     }
  110.     deep[1] = 1; dfs1(1, 0);
  111.     dfs2(1, 1);
  112. /*    for(int i = 1; i <= N; i++)    
  113.         for(int j = 1; j <= i - 1; j++)
  114.             printf("%d %d %d\n", i, j, GetLca(i, j));*/
  115.     DealAsk();
  116.     Mo();
  117.     return 0;
  118. }

数学

莫比乌斯反演

  1. #include<bits/stdc++.h>
  2. // #define int long long
  3. using namespace std;
  4. const int MAXN = 1e6 + 10, mod = 1000000007, mod2 = mod - 1;
  5. template<typename A, typename B> inline int add(A x, B y) {
  6.     if(x + y < 0) return x + y + mod;
  7.     else return x + y >= mod ? x + y - mod : x + y;
  8. }
  9. template<typename A, typename B> inline int mul(A x, B y) {
  10.     return 1ll * x * y % mod;
  11. }
  12. template<typename A, typename B> inline void mul2(A &x, B y) {
  13.     x = 1ll * x * y % mod;
  14. }
  15. inline int read() {
  16.     char c = getchar(); int x = 0, f = 1;
  17.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  18.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  19.     return x * f;
  20. }
  21. int f[MAXN], g[MAXN], vis[MAXN], prime[MAXN], mu[MAXN], tot;
  22. int fp(int a, int p, int mod) {
  23.     int base = 1;
  24.     while(p) {
  25.         if(p & 1) base = 1ll * base * a % mod;
  26.         a = 1ll * a * a % mod; p >>= 1;
  27.     }
  28.     return base;
  29. }
  30. int inv(int x) {
  31.     if(x == 0) return 1;
  32.     return fp(x, mod - 2, mod);
  33. }
  34. void sieve(int N) {
  35.     f[0] = 0; f[1] = 1;
  36.     for(int i = 2; i <= N; i++) f[i] = add(f[i - 1], f[i - 2]);
  37.     vis[1] = 1; mu[1] = 1; 
  38.     for(int i = 2; i <= N; i++) {
  39.         if(!vis[i]) prime[++tot] = i, mu[i] = -1;
  40.         for(int j = 1; j <= tot && i * prime[j] <= N; j++) {
  41.             vis[i * prime[j]] = 1;
  42.             if(i % prime[j]) mu[i * prime[j]] = -mu[i];
  43.             else {mu[i * prime[j]] = 0; break;}
  44.         }
  45.     }
  46.     fill(g + 1, g + N + 1, 1);
  47.     for(int d = 1; d <= N; d++) {
  48.         int t1 = fp(f[d], mod2 - 1, mod), t2 = f[d];
  49.         for(int T = d; T <= N; T += d) {
  50.             if(mu[T / d] == -1) g[T] = mul(g[T],t1);
  51.             else if(mu[T / d] == 1) g[T] = mul(g[T], f[d]);
  52.         }
  53.     }
  54.     g[0] = 1;
  55.     for(int i = 1; i <= N; i++) mul2(g[i], g[i - 1]);
  56. }
  57. int N, M, pre;
  58. void solve() {
  59.     N = read(); M = read();
  60.     if(N > M) swap(N, M);
  61.     int ans = 1, tmp;
  62.     for(int i = 1, j; i <= N; i = j + 1) {
  63.         j = min(N / (N / i), M / (M / i));
  64.         mul2(ans, fp(mul(g[j], inv(g[i - 1])), 1ll * (N / i) * (M / i) % mod2, mod));
  65.     }
  66.     cout << ans << '\n'; 
  67. }
  68. signed main() {
  69.     sieve(1e6);
  70.     int T = read();
  71.     pre = T;
  72.     for(; T; T--, solve());
  73.     return 0;
  74. }

杜教筛

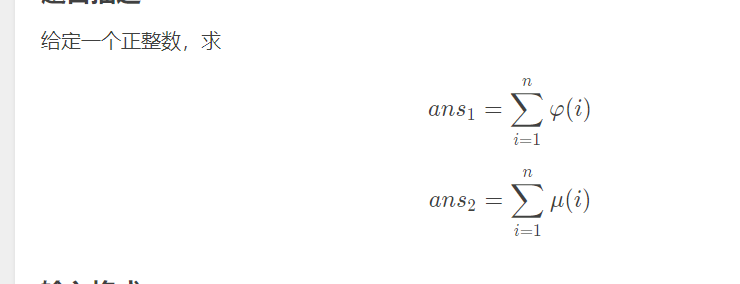
  1. #include <algorithm>
  2. #include <cmath>
  3. #include <cstdio>
  4. #include <cstring>
  5. #include <map>
  6. #define LL long long
  7. using namespace std;
  8. const int MAXN = 5000030;
  9. inline int read() {
  10.     char c = getchar();
  11.     int x = 0, f = 1;
  12.     while (c < '0' || c > '9') {
  13.         if (c == '-') f = -1;
  14.         c = getchar();
  15.     }
  16.     while (c >= '0' && c <= '9') {
  17.         x = x * 10 + c - '0';
  18.         c = getchar();
  19.     }
  20.     return x * f;
  21. }
  22. int N, limit = 5000000, tot = 0, vis[MAXN], mu[MAXN], prime[MAXN];
  23. LL phi[MAXN];
  24. void GetMuAndPhi() {
  25.     vis[1] = 1;
  26.     phi[1] = 1;
  27.     mu[1] = 1;
  28.     for (int i = 1; i <= limit; i++) {
  29.         if (!vis[i]) prime[++tot] = i, phi[i] = i - 1, mu[i] = -1;
  30.         for (int j = 1; j <= tot && i * prime[j] <= limit; j++) {
  31.             vis[i * prime[j]] = 1;
  32.             if (i % prime[j] == 0) {
  33.                 mu[i * prime[j]] = 0;
  34.                 phi[i * prime[j]] = phi[i] * prime[j];
  35.                 break;
  36.             } else {
  37.                 mu[i * prime[j]] = -mu[i];
  38.                 phi[i * prime[j]] = phi[i] * (prime[j] - 1);
  39.             }
  40.         }
  41.     }
  42.     for (int i = 1; i <= limit; i++) mu[i] += mu[i - 1], phi[i] += phi[i - 1];
  43. }
  44. map<int, LL> Aphi, Amu;
  45. LL SolvePhi(LL n) {
  46.     if (n <= limit) return phi[n];
  47.     if (Aphi[n]) return Aphi[n];
  48.     LL tmp;
  49.     if (n & 1)
  50.         tmp = (n + 1) / 2LL * n;
  51.     else
  52.         tmp = n / 2LL * (n + 1);
  53.     for (int i = 2, nxt; i <= N; i = nxt + 1) {
  54.         nxt = min(n, n / (n / i));
  55.         tmp -= SolvePhi(n / i) * (LL)(nxt - i + 1);
  56.         if (nxt == n) break;
  57.     }
  58.     return Aphi[n] = tmp;
  59. }
  60. LL SolveMu(LL n) {
  61.     if (n <= limit) return mu[n];
  62.     if (Amu[n]) return Amu[n];
  63.     LL tmp = 1;
  64.     for (int i = 2, nxt; i <= N; i = nxt + 1) {
  65.         nxt = min(n, n / (n / i));
  66.         tmp -= SolveMu(n / i) * (LL)(nxt - i + 1);
  67.         if (nxt == n) break;
  68.     }
  69.     return Amu[n] = tmp;
  70. }
  71. int main() {
  72. #ifdef WIN32
  73.     freopen("a.in", "r", stdin);
  74. #else
  75. #endif
  76.     GetMuAndPhi();
  77.     int QWQ;
  78.     scanf("%d", &QWQ);
  79.     while (QWQ--) {
  80.         scanf("%lld", &N);
  81.         printf("%lld %lld\n", SolvePhi(N), SolveMu(N));
  82.     }
  83.     return 0;
  84. }

BSGS

  1. #include<bits/stdc++.h> 
  2. #define Pair pair<int, int>
  3. #define MP(x, y) make_pair(x, y)
  4. #define fi first
  5. #define se second
  6. #define int long long 
  7. #define LL long long 
  8. #define ull unsigned long long 
  9. #define Fin(x) {freopen(#x".in","r",stdin);}
  10. #define Fout(x) {freopen(#x".out","w",stdout);}
  11. using namespace std;
  12. const int MAXN = 1e6 + 10, INF = 1e9 + 10;;
  13. int mod;
  14. const double eps = 1e-9;
  15. template <typename A, typename B> inline bool chmin(A &a, B b){if(a > b) {a = b; return 1;} return 0;}
  16. template <typename A, typename B> inline bool chmax(A &a, B b){if(a < b) {a = b; return 1;} return 0;}
  17. template <typename A, typename B> inline LL add(A x, B y) {if(x + y < 0) return x + y + mod; return x + y >= mod ? x + y - mod : x + y;}
  18. template <typename A, typename B> inline void add2(A &x, B y) {if(x + y < 0) x = x + y + mod; else x = (x + y >= mod ? x + y - mod : x + y);}
  19. template <typename A, typename B> inline LL mul(A x, B y) {return 1ll * x * y % mod;}
  20. template <typename A, typename B> inline void mul2(A &x, B y) {x = (1ll * x * y % mod + mod) % mod;}
  21. template <typename A> inline void debug(A a){cout << a << '\n';}
  22. template <typename A> inline LL sqr(A x){return 1ll * x * x;}
  23. template <typename A, typename B> inline LL fp(A a, B p, int md = mod) {int b = 1;while(p) {if(p & 1) b = mul(b, a);a = mul(a, a); p >>= 1;}return b;}
  24. template <typename A> A inv(A x) {return fp(x, mod - 2);}
  25. inline int read() {
  26.     char c = getchar(); int x = 0, f = 1;
  27.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  28.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  29.     return x * f;
  30. }
  31. int a, b, X1, End;
  32. //x_{i+1} = (aX_i + b) % P
  33. //a^ans = x % p
  34. //a^{i * k - j} = x % p
  35. //a^{i * k} = x * a^j % p
  36. map<int, int> mp;
  38. /*
  39. int Query(int a, int x, int p) {
  40.     if(__gcd(a, p) != 1) return -2;
  41.     int base = 1;
  42.     for(int i = 0; i <= p; i++) {
  43.         if(base % p == x) return i;
  44.         mul2(base, a);
  45.     }
  46.     return -2;
  47. }
  48. */
  50. int Query(int a, int x, int p) {
  51.     if(__gcd(a, p) != 1) return -2;
  52.     mp.clear(); int block = ceil(sqrt(p)), base = fp(a, block);
  53.     for(int i = 0, cur = x; i <= block; i++, mul2(cur, a)) mp[cur] = i;
  54.     for(int i = 1, cur = base; i <= block; i++, mul2(cur, base)) 
  55.         if(mp[cur]) 
  56.             return i * block - mp[cur];
  57.     return -2;
  58. }
  60. void solve() {
  61.     mod = read(); a = read(); b = read(); X1 = read(); End = read();
  62.     if(X1 == End) {puts("1"); return ;}
  63.     if(!a) {
  64.         if(!b) {puts(End == X1 ? "1" : "-1");return ;}
  65.         else {puts(End == b ? "2" : "-1");return ;}
  66.     }
  67.     if(a == 1) {
  68.         if(!b) {puts(End == X1 ? "1" : "-1");return ;}
  69.         else {
  70.             //int tmp = add(End, -X1 + mod) % b;
  71.             //cout << tmp << '\n';
  72.             cout << mul(add(End, -X1), inv(b)) + 1 << '\n'; 
  73.             return ;
  74.         }
  75.     }
  76.     int tmp = mul(b, inv(a - 1));
  77.     add2(X1, tmp); add2(End, tmp); 
  78.     mul2(End, inv(X1));
  79.     cout << Query(a, End, mod) + 1 << '\n';
  80. }
  81. signed main() {
  82.     //freopen("a.in", "r", stdin);
  83.     for(int T = read(); T--; solve());
  84.     return 0;
  85. }

exgcd

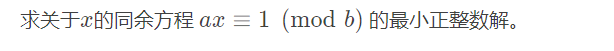
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. inline int read() {
  4.     int x; cin >> x; return x;
  5. }
  6. int a, b, x, y;
  7. int exgcd(int a, int b, int &x, int &y) {
  8.     if(!b)  {x = 1; y = 0; return a;}
  9.     int r = exgcd(b, a % b, x, y);
  10.     int t = x; x = y, y = t - a / b * y;
  11.     return r;
  12. }
  13. int main() {
  14.     a = read(); b = read();
  15.     int r = exgcd(a, b, x, y);
  16.     while(x < 0) x += b;
  17.     cout << x;
  18.     return 0;
  19. }

Lucas

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int MAXN = 2e5 + 10;
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M, mod;
  11. int mul(int x, int y) {return 1ll * x * y % mod;}
  12. int add(int x, int y) {return (x + y + mod) % mod;}
  13. int mul2(int &x, int y) {x = 1ll * x * y % mod;}
  14. int add2(int &x, int y) {x = (x + y + mod) % mod;}
  15. int fp(int a, int p) {
  16.     int base = 1;
  17.     while(p) {
  18.         if(p & 1) base = mul(base, a);
  19.         a = mul(a, a); p >>= 1;
  20.     }
  21.     return base;
  22. }
  23. int fac[MAXN], ifac[MAXN];
  24. int C(int N, int M) {
  25.     if(N < M) return 0;
  26.     if((!N) || (!M)) return 1;
  27.     return mul(fac[N], mul(ifac[M], ifac[N - M]));
  28. }
  29. int Lucas(int N, int M) {
  30.     if(!N || !M) return 1;
  31.     if(N < M) return 0;
  32.     return mul(Lucas(N / mod, M / mod), C(N % mod, M % mod));
  33. }
  34. int main() {
  35.     int T = read();
  36.     while(T--) {
  37.         N = read(); M = read(); N += M; mod = read();
  38.         fac[0] = 1; int Lim = mod - 1;
  39.         for(int i = 1; i <= Lim; i++) fac[i] = mul(fac[i - 1], i);
  40.         ifac[Lim] = fp(fac[Lim], mod - 2); 
  41.         for(int i = Lim; i >= 1; i--) ifac[i - 1] = mul(ifac[i], i);
  42.         cout << Lucas(N, M) << '\n';
  43.     }
  44.     return 0;
  45. }
  46. /*
  47. 2
  48. 2132 1311 91431
  49. 1 2 5
  51. */

miller-rabin

  1. // luogu-judger-enable-o2
  2. #include<cstdio>
  3. #define LL long long 
  4. inline int read() {
  5.     char c = getchar(); int x = 0, f = 1;
  6.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  7.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  8.     return x * f;
  9. }
  10. int N, M, Test[10] = {2, 3, 5, 7, 11, 13, 17};
  11. int pow(int a, int p, int mod) {
  12.     int base = 1;
  13.     for(; p; p >>= 1, a = (1ll * a * a) % mod) 
  14.         if(p & 1) base = (1ll * base * a) % mod;
  15.     return base % mod;
  16. }
  17. bool Query(int P) {
  18.     if(P == 1) return 0;
  19.     int t = P - 1, k = 0;
  20.     while(!(t & 1)) k++, t >>= 1;
  21.     for(int i = 0; i < 4; i++) {
  22.         if(P == Test[i]) return 1;
  23.         LL a = pow(Test[i], t, P), nxt = a;
  24.         for(int j = 1; j <= k; j++) {
  25.             nxt = (a * a) % P;
  26.             if(nxt == 1 && a != 1 && a != P - 1) return 0;
  27.             a = nxt;
  28.         }
  29.         if(a != 1) return 0;
  30.     }
  31.     return 1;
  32. }
  33. main() { 
  34.     N = read(); M = read();    
  35.     while(M--) puts(Query(read()) ? "Yes" : "No");
  36. }

多项式

NTT

  1. // luogu-judger-enable-o2
  2. #include<bits/stdc++.h>
  3. using namespace std;
  4. const int MAXN = 6e6 + 10, mod = 998244353, G = 3, Gi = 332748118;
  5. inline int read() {
  6.     char c = getchar(); int x = 0, f = 1;
  7.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  8.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  9.     return x * f;
  10. }
  11. int N, M, a[MAXN], b[MAXN], r[MAXN];
  12. int mul(int x, int y) {
  13.     return 1ll * x * y % mod;
  14. }
  15. int add(int x, int y) {
  16.     return x + y >= mod ? x + y - mod : x + y;
  17. }
  18. int fp(int a, int p) {
  19.     int base = 1;
  20.     while(p) {
  21.         if(p & 1) base = mul(base, a);
  22.         a = mul(a, a); p >>= 1;
  23.     }
  24.     return base;
  25. }
  26. void NTT(int *A, int lim, int opt) {
  27.     for(int i = 0; i <= lim; i++) if(i < r[i]) swap(A[i], A[r[i]]);
  28.     for(int mid = 1; mid < lim; mid <<= 1) {
  29.         int wn = fp(opt == 1 ? G : Gi, (mod - 1) / (mid << 1));
  30.         for(int i = 0; i < lim; i += (mid << 1)) {
  31.             int w = 1; 
  32.             for(int j = 0; j < mid; j++, w = mul(w, wn)) {
  33.                 int x = A[i + j], y = mul(w, A[i + j + mid]);
  34.                 A[i + j] = add(x, y);
  35.                 A[i + mid + j] = add(x, mod - y);
  36.             }
  37.         }
  38.     }
  39.     if(opt == -1) {
  40.         int inv = fp(lim, mod - 2);
  41.         for(int i = 0; i <= lim; i++) {
  42.             a[i] = mul(a[i], inv);  
  43.         }
  44.     }
  45. }
  46. int main() {
  47.     N = read(); M = read();
  48.     for(int i = 0; i <= N; i++) a[i] = read();
  49.     for(int i = 0; i <= M; i++) b[i] = read();
  50.     int lim = 1, l = 0;
  51.     while(lim <= N + M) lim <<= 1, l++;
  52.     for(int i = 1; i <= lim; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
  53.     NTT(a, lim, 1); 
  54.     NTT(b, lim, 1);
  55.     for(int i = 0; i <= lim; i++) a[i] = mul(a[i], b[i]);
  56.     NTT(a, lim, -1);
  57.     for(int i = 0; i <= N + M; i++) cout << a[i] << ' ';
  58.     return 0;
  59. }

FFT

  1. // luogu-judger-enable-o2
  2. #include<iostream>
  3. #include<cstdio>
  4. #include<cmath>
  5. using namespace std;
  6. const int MAXN = 1e7 + 10;
  7. inline int read() {
  8.     char c = getchar(); int x = 0, f = 1;
  9.     while (c < '0' || c > '9') {if (c == '-')f = -1; c = getchar();}
  10.     while (c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}
  11.     return x * f;
  12. }
  13. const double Pi = acos(-1.0);
  14. struct complex {
  15.     double x, y;
  16.     complex (double xx = 0, double yy = 0) {x = xx, y = yy;}
  17. } a[MAXN], b[MAXN];
  18. complex operator + (complex a, complex b) { return complex(a.x + b.x , a.y + b.y);}
  19. complex operator - (complex a, complex b) { return complex(a.x - b.x , a.y - b.y);}
  20. complex operator * (complex a, complex b) { return complex(a.x * b.x - a.y * b.y , a.x * b.y + a.y * b.x);} //不懂的看复数的运算那部分
  21. int N, M;
  22. int l, r[MAXN];
  23. int limit = 1;
  24. void fast_fast_tle(complex *A, int type) {
  25.     for (int i = 0; i < limit; i++)
  26.         if (i < r[i]) swap(A[i], A[r[i]]); //求出要迭代的序列
  27.     for (int mid = 1; mid < limit; mid <<= 1) { //待合并区间的长度的一半
  28.         complex Wn( cos(Pi / mid) , type * sin(Pi / mid) ); //单位根
  29.         for (int R = mid << 1, j = 0; j < limit; j += R) { //R是区间的长度，j表示前已经到哪个位置了
  30.             complex w(1, 0); //幂
  31.             for (int k = 0; k < mid; k++, w = w * Wn) { //枚举左半部分
  32.                 complex x = A[j + k], y = w * A[j + mid + k]; //蝴蝶效应
  33.                 A[j + k] = x + y;
  34.                 A[j + mid + k] = x - y;
  35.             }
  36.         }
  37.     }
  38. }
  39. int main() {
  40.     int N = read(), M = read();
  41.     for (int i = 0; i <= N; i++) a[i].x = read();
  42.     for (int i = 0; i <= M; i++) b[i].x = read();
  43.     while (limit <= N + M) limit <<= 1, l++;
  44.     for (int i = 0; i < limit; i++)
  45.         r[i] = ( r[i >> 1] >> 1 ) | ( (i & 1) << (l - 1) ) ;
  46.     // 在原序列中 i 与 i/2 的关系是 ： i可以看做是i/2的二进制上的每一位左移一位得来
  47.     // 那么在反转后的数组中就需要右移一位，同时特殊处理一下奇数
  48.     fast_fast_tle(a, 1);
  49.     fast_fast_tle(b, 1);
  50.     for (int i = 0; i <= limit; i++) a[i] = a[i] * b[i];
  51.     fast_fast_tle(a, -1);
  52.     for (int i = 0; i <= N + M; i++)
  53.         printf("%d ", (int)(a[i].x / limit + 0.5));
  54.     return 0;
  55. }

常系数齐次线性递推

  1. // luogu-judger-enable-o2
  2. #include<bits/stdc++.h> 
  3. #define Pair pair<int, int>
  4. #define MP(x, y) make_pair(x, y)
  5. #define fi first
  6. #define se second
  7. #define LL long long 
  8. #define ull unsigned long long 
  9. #define Fin(x) {freopen(#x".in","r",stdin);}
  10. #define Fout(x) {freopen(#x".out","w",stdout);}
  11. using namespace std;
  12. const int MAXN = 4e5 + 10, INF = 1e9 + 10, INV2 = 499122177;
  13. const double eps = 1e-9, pi = acos(-1);
  14. const int G = 3, mod = 998244353;
  15. inline int read() {
  16.     char c = getchar(); int x = 0, f = 1;
  17.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  18.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  19.     return x * f;
  20. }
  21. namespace Poly {
  22.     int rev[MAXN], GPow[MAXN], A[MAXN], B[MAXN], C[MAXN], lim;
  23.     template <typename A, typename B> inline LL add(A x, B y) {if(x + y < 0) return x + y + mod; return x + y >= mod ? x + y - mod : x + y;}
  24.     template <typename A, typename B> inline void add2(A &x, B y) {if(x + y < 0) x = x + y + mod; else x = (x + y >= mod ? x + y - mod : x + y);}
  25.     template <typename A, typename B> inline LL mul(A x, B y) {return 1ll * x * y % mod;}
  26.     template <typename A, typename B> inline void mul2(A &x, B y) {x = (1ll * x * y % mod + mod) % mod;}
  27.     int fp(int a, int p, int P = mod) {
  28.         int base = 1;
  29.         for(; p; p >>= 1, a = 1ll * a * a % P) if(p & 1) base = 1ll * base *  a % P;
  30.         return base;
  31.     }
  32.     int GetLen(int x) {
  33.         int lim = 1;
  34.         while(lim < x) lim <<= 1;
  35.         return lim;
  36.     }
  37.     int GetLen2(int x) {
  38.         int lim = 1; 
  39.         while(lim <= x) lim <<= 1;
  40.         return lim;
  41.     }
  42.     int GetOrigin(int x) {//¼ÆËãÔ­¸ù 
  43.         static int q[MAXN]; int tot = 0, tp = x - 1;
  44.         for(int i = 2; i * i <= tp; i++) if(!(tp % i)) {q[++tot] = i;while(!(tp % i)) tp /= i;}
  45.         if(tp > 1) q[++tot] = tp;
  46.         for(int i = 2, j; i <= x - 1; i++) {
  47.             for(j = 1; j <= tot; j++) if(fp(i, (x - 1) / q[j], x) == 1) break;
  48.             if(j == tot + 1) return i;
  49.         }
  50.     }
  51.     void Init(int Lim) {
  52.         for(int i = 1; i <= Lim; i++) GPow[i] = fp(G, (mod - 1) / i);
  53.     }
  54.     void NTT(int *A, int lim, int opt) {
  55.         int len = 0; for(int N = 1; N < lim; N <<= 1) ++len; 
  56.         for(int i = 1; i <= lim; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (len - 1));
  57.         for(int i = 0; i <= lim; i++) if(i < rev[i]) swap(A[i], A[rev[i]]);
  58.         for(int mid = 1; mid < lim; mid <<= 1) {
  59.             int Wn = GPow[mid << 1];
  60.             for(int i = 0; i < lim; i += (mid << 1)) {
  61.                 for(int j = 0, w = 1; j < mid; j++, w = mul(w, Wn)) {
  62.                     int x = A[i + j], y = mul(w, A[i + j + mid]);
  63.                     A[i + j] = add(x, y), A[i + j + mid] = add(x, -y);
  64.                 }
  65.             }
  66.         }
  67.         if(opt == -1) {
  68.             reverse(A + 1, A + lim);
  69.             int Inv = fp(lim, mod - 2);
  70.             for(int i = 0; i <= lim; i++) mul2(A[i], Inv);
  71.         }
  72.     }
  73.     void Mul(int *a, int *b, int N, int M) {
  74.         memset(A, 0, sizeof(A)); memset(B, 0, sizeof(B));
  75.         int lim = 1, len = 0; 
  76.         while(lim <= N + M) len++, lim <<= 1;
  77.         for(int i = 0; i <= N; i++) A[i] = a[i]; 
  78.         for(int i = 0; i <= M; i++) B[i] = b[i];
  79.         NTT(A, lim, 1); NTT(B, lim, 1);
  80.         for(int i = 0; i <= lim; i++) B[i] = mul(B[i], A[i]);
  81.         NTT(B, lim, -1);
  82.         for(int i = 0; i <= N + M; i++) b[i] = B[i];
  83.         memset(A, 0, sizeof(A)); memset(B, 0, sizeof(B));
  84.     }
  85.     void Inv(int *a, int *b, int len) {//B1 = 2B - A1 * B^2 
  86.         if(len == 1) {b[0] = fp(a[0], mod - 2); return ;}
  87.         Inv(a, b, len >> 1);
  88.         for(int i = 0; i < len; i++) A[i] = a[i], B[i] = b[i];
  89.         NTT(A, len << 1, 1); NTT(B, len << 1, 1);
  90.         for(int i = 0; i < (len << 1); i++) mul2(A[i], mul(B[i], B[i]));
  91.         NTT(A, len << 1, -1);
  92.         for(int i = 0; i < len; i++) add2(b[i], add(b[i], -A[i]));
  93.         for(int i = 0; i < (len << 1); i++) A[i] = B[i] = 0;
  94.     }
  95.     void Dao(int *a, int *b, int len) {
  96.         for(int i = 1; i < len; i++) b[i - 1] = mul(i, a[i]); b[len - 1] = 0;
  97.     }
  98.     void Ji(int *a, int *b, int len) {
  99.         for(int i = 1; i < len; i++) b[i] = mul(a[i - 1], fp(i, mod - 2)); b[0] = 0;
  100.     }
  101.     void Ln(int *a, int *b, int len) {//G(A) = \frac{A}{A'} qiudao zhihou jifen 
  102.         static int A[MAXN], B[MAXN];
  103.         Dao(a, A, len); 
  104.         Inv(a, B, len);
  105.         NTT(A, len << 1, 1); NTT(B, len << 1, 1);
  106.         for(int i = 0; i < (len << 1); i++) B[i] = mul(A[i], B[i]);
  107.         NTT(B, len << 1, -1); 
  108.         Ji(B, b, len << 1);
  109.         memset(A, 0, sizeof(A)); memset(B, 0, sizeof(B));
  110.     }
  111.     void Exp(int *a, int *b, int len) {//F(x) = F_0 (1 - lnF_0 + A) but code ..why....
  112.         if(len == 1) return (void) (b[0] = 1);
  113.         Exp(a, b, len >> 1); Ln(b, C, len);
  114.         C[0] = add(a[0] + 1, -C[0]);
  115.         for(int i = 1; i < len; i++) C[i] = add(a[i], -C[i]);
  116.         NTT(C, len << 1, 1); NTT(b, len << 1, 1);
  117.         for(int i = 0; i < (len << 1); i++) mul2(b[i], C[i]);
  118.         NTT(b, len << 1, -1);
  119.         for(int i = len; i < (len << 1); i++) C[i] = b[i] = 0;
  120.     }
  121.     void Sqrt(int *a, int *b, int len) {
  122.         static int B[MAXN];
  123.         Ln(a, B, len);
  124.         for(int i = 0; i < len; i++) B[i] = mul(B[i], INV2);
  125.         Exp(B, b, len); 
  126.     }
  127.     void Div(int *F, int *G, int *Q, int *R, int N, int M) {//F(n) = G(m) * Q(n - m + 1) + R(m) 
  128.         static int Ginv[MAXN], TF[MAXN], TG[MAXN]; memset(Ginv, 0, sizeof(Ginv));
  129.         memcpy(TF, F, (N + 1) << 2); memcpy(TG, G, (M + 1) << 2);
  131.         reverse(F, F + N + 1); reverse(G, G + M + 1);
  132.         Inv(G, Ginv, GetLen2(N - M));//why not M
  133.         Mul(F, Ginv, N - M, N - M);
  134.         for(int i = 0; i <= N - M; i++) Q[i] = Ginv[i];
  135.         reverse(Q, Q + N - M + 1);
  136.         reverse(F, F + N + 1); reverse(G, G + M + 1);
  137.         Mul(Q, G, N - M, M);
  138.         for(int i = 0; i < M; i++) R[i] = add(F[i], -G[i]);
  139.         memcpy(F, TF, (N + 1) << 2); memcpy(G, TG, (M + 1) << 2);
  140.     }
  141.     void PowNum(int *a, int *b, int P, int N, int len) {
  142.         static int tx[MAXN], ty[MAXN]; memset(tx, 0, sizeof(tx)); memset(ty, 0, sizeof(ty));
  143.         Ln(a, tx, len);
  144.         for(int i = 0; i < N; i++) ty[i] = mul(P, tx[i]);
  145.         Exp(ty, b, len);
  146.     }
  147.     void MOD(int *A,  int *B, int n, int m) {
  148.         static int Q[MAXN], R[MAXN];
  149.         Div(A, B, Q, R, n, m);
  150.         memcpy(A, R, m << 2);
  151.     }
  152.     void PowPoly(int *base, LL p, int *Mod, int m) {
  153.         static int res[MAXN], T[MAXN]; res[0] = 1;
  154.         while(p) {
  155.             if(p & 1) {
  156.                 int lim = GetLen(m << 1);
  157.                 memset(res + m, 0, lim - m << 2);;
  158.                 memcpy(T, base, m << 2); memset(T + m, 0, lim - m << 2);
  159.                 //Mul(T, res, lim, lim);
  160.                 NTT(T, lim, 1); NTT(res, lim, 1);
  161.                 for(int i = 0; i < lim; i++) res[i] = mul(res[i], T[i]);
  162.                 NTT(res, lim, -1); 
  163.                 MOD(res, Mod, lim, m);
  164.             }
  165.             p >>= 1;
  166.             if(p) {
  167.                 int lim = GetLen(m << 1);
  168.                 memset(base + m, 0, lim - m << 2);
  169.                 NTT(base, lim, 1); 
  170.                 for(int i = 0; i < lim; i++) base[i] = mul(base[i], base[i]);
  171.                 NTT(base, lim, -1); 
  172.                 MOD(base, Mod, (m << 1) , m);
  173.             }
  174.         }
  175.         memcpy(base, res, m << 2);
  176.     }
  177.     int solve(int *f, int *a, LL n, int k) {
  178.         static int AA[MAXN], G[MAXN];
  179.         for(int i = 1; i <= k; i++) G[k - i] = (-f[i] + mod) % mod;
  180.         G[k] = AA[1] = 1;
  181.         PowPoly(AA, n, G, k);
  182.         int ans = 0;
  183.         for(int i = 0; i < k; i++) add2(ans, mul(AA[i], a[i]) - mod);
  184.         return ans;
  185.     }
  186.     int LRec(LL N, int K) {//a_n = \sum_{i=1}^k f_i * a_{n-i}
  187.         static int f[MAXN], a[MAXN];
  188.         Init(8 * K);
  189.         for(int i = 1; i <= K; i++) f[i] = read();
  190.         for(int i = 0; i < K; i++)  a[i] = (read() + mod) % mod;
  191.         return solve(f, a, N, K);
  192.     }
  193. };
  194. using namespace Poly; 
  195. signed main() {
  196.     //freopen("testdata.in", "r", stdin);
  197.     LL N = read();int K = read();
  198.     cout << LRec(N, K);
  199.     return 0;
  200. }

计算几何

二维凸包

  1. // luogu-judger-enable-o2
  2. #include<cstdio>
  3. #include<cmath>
  4. #include<algorithm>
  5. using namespace std;
  6. const int eps = 1e-10;
  7. int dcmp(double x) {
  8.     if(fabs(x) < eps) return 0;
  9.     return x < 0 ? -1 : 1;
  10. }
  11. #define Point Vector 
  12. struct Vector {
  13.     double x, y;
  14.     Vector(double x = 0, double y = 0) : x(x), y(y) {};
  15.     bool operator < (const Vector &rhs) const {
  16.         return dcmp(x - rhs.x) == 0 ? y < rhs.y : x < rhs.x;
  17.     }
  18.     Vector operator - (const Vector &rhs) const {
  19.         return Vector(x - rhs.x, y - rhs.y);
  20.     }
  21. };
  22. double Cross(Vector A, Vector B) {
  23.     return A.x * B.y - A.y * B.x; 
  24. }
  25. double dis(Point a, Point b) {
  26.     return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
  27. }
  28. int N; 
  29. Point p[10001], q[10001];
  30. int top;
  31. void Push(Point p) {
  32.     while(Cross(q[top] - q[top - 1], p - q[top - 1]) < 0) top--;
  33.     q[++top] = p;
  34. }
  35. void Andrew() {
  36.     q[0] = q[top = 1] = p[1];
  37.     for(int i = 2; i <= N; i++) Push(p[i]);
  38.     for(int i = N - 1; i; --i)  Push(p[i]);
  39. }
  40. int main() {    
  41.     scanf("%d", &N);
  42.     for(int i = 1; i <= N; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
  43.     sort(p + 1, p + N + 1);
  44.     Andrew();
  45.     double ans = 0;
  46.     for(int i = 1; i < top; i++)
  47.         ans += dis(q[i], q[i + 1]);
  48.     printf("%.2lf", ans);
  49.     return 0;
  50. }

其他

模拟退火

  1. /*
  2. */
  3. #include<iostream>
  4. #include<cstdio>
  5. #include<cmath>
  6. #include<cstdlib>
  7. #include<ctime>
  8. #include<cstring>
  9. #include<algorithm>
  10. #include<vector>
  11. #define Pair pair<int, int> 
  12. #define MP(x, y) make_pair(x, y)
  13. #define fi first
  14. #define se second
  15. using namespace std;
  16. const int MAXN = 1001;
  17. const double eps = 1e-10, Dlt = 0.97, INF = 1e9 + 7;
  18. inline int read() {
  19.     char c = getchar(); int x = 0, f = 1;
  20.     while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
  21.     while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
  22.     return x * f;
  23. }
  24. int N, M;
  25. struct Edge {
  26.     int u, v, w;
  27.     bool operator < (const Edge &rhs) const {
  28.         return w < rhs.w;
  29.     }
  30. }E[MAXN];
  31. int link[MAXN][MAXN], num, fa[MAXN];
  32. void unionn(int x, int y) {
  33.     fa[x] = y;
  34. }
  35. int find(int x) {
  36.     if(fa[x] == x) return fa[x];
  37.     else return fa[x] = find(fa[x]);
  38. }
  39. vector<Pair> v[MAXN];
  40. int dfs(int x, int cnt, int fa) {
  41.     int ans = 0;
  42.     for(int i = 0; i < v[x].size(); i++) {
  43.         int to = v[x][i].fi, w = v[x][i].se;
  44.         if(to != fa) ans += dfs(to, cnt + 1, x) + w * cnt;
  45.     }
  46.     return ans;
  47. }
  48. int solve() {
  49.     int cur = INF, tot = 0, base = 0;
  50.     for(int i = 1; i <= N; i++) fa[i] = i, v[i].clear();
  51.     for(int i = 1; i <= M; i++) {
  52.         int x = E[i].u, y = E[i].v;
  53.         int fx = find(x), fy = find(y);
  54.         if(fx == fy) continue;
  55.         tot++; unionn(fx, fy); 
  56.         v[x].push_back(MP(y, E[i].w));
  57.         v[y].push_back(MP(x, E[i].w));
  58.     }
  59.     if(tot != N - 1) return INF;
  60.     for(int i = 1; i <= N; i++)
  61.         cur = min(cur, dfs(i, 1, 0));
  62.     return cur;
  63. }
  64. int main() {
  65. //    freopen("testdata.in", "r", stdin);
  66.     srand((unsigned)time(NULL));
  67.     memset(link, 0x7f, sizeof(link));
  68.     N = read(); M = read();
  69.     if(N == 1) {
  70.         puts("0"); return 0;
  71.     }
  72.     for(int i = 1; i <= M; i++) {
  73.         int x = read(), y = read(), w = read();
  74.         link[x][y] = min(link[x][y], w);
  75.         link[y][x] = min(link[y][x], w);
  76.     }
  77.     for(int i = 1; i <= N; i++) 
  78.         for(int j = i + 1; j <= N; j++) 
  79.             if(link[i][j] <= INF) 
  80.                 E[++num] = (Edge) {i, j, link[i][j]};
  81.     sort(E + 1, E + num + 1);
  82.     int ans = solve();
  83.     int times = 200;
  84.     while(times--) {
  85.         int now = INF;
  86.         for(double T = 100000; T > eps; T *= Dlt) {
  87.             int x = rand() % num + 1, y = rand() % num + 1;
  88.             //check(x, y);
  89.             swap(E[x], E[y]);
  90.             int nxt = solve();
  91.             if(nxt < ans) {ans = nxt; continue;}
  92.             if(nxt < now || ((exp(now - nxt / T) < rand() / RAND_MAX))) {now = nxt; continue;}
  93.             swap(E[x], E[y]);
  94.         }
  95.     }
  96.     printf("%d", ans);
  97.     return 0;
  98. }
添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注