$$\text{解题报告}$$

T1 括号

30-40做法：

将括号序列的每个子序列选出，判断是否合理，暴力搜索匹配括号。时间复杂度$O(2^n)$

60分做法：

这就需要研究一下，题目中所给的大数据了，因为有特殊条件限制，大数据比起前面的数据更好拿分，想一想左括号全部在右括号左侧的话，我们可以考虑贪心，讲左括号部分与右括号部分价值处理出来，然后排一下序，当然谁大选谁了。

100分：

其实题目中的大部分数据已经解决了，现在我们需要考虑对于$n\le 2000$的范围考虑，考虑DP了。
设$DP[i][]j$为考虑了前i个括号，目前有j个左括号待匹配的最大权值和，那么转移的话分以下两种情况：

$$DP[i][j]=max(DP[i-1][j],DP[i-1][j-1]+a_j),(s_i='(')$$
$$DP[i][j]=max(DP[i-1][j],DP[i-1][j+1]+a_j),(s_i=')')$$
注意一下边界就好了，最后答案是$DP[n][0]$
时间复杂度：$O(n^2)$

代码

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
#define N 200000 + 5
#define INF 0x3f3f3f3f
int n, ans, A[N];
char s[N];
namespace DP
{
    int Dp[2][N];
    void Init()
    {
        Dp[0][0] = 0;
        for (int i = 1; i <= n; i ++)
            Dp[0][i] = -INF;
    }
    int Solve()
    {
        Init();
        for (int l = 1; l <= n; l ++)
        {
            for (int i = 0; i <= n; i ++)
            {
                Dp[1][i] = Dp[0][i];
                if (s[l] == '(' && i)
                    Dp[1][i] = max(Dp[1][i], Dp[0][i - 1] + A[l]);
                else if (s[l] == ')' && i < n)
                    Dp[1][i] = max(Dp[1][i], Dp[0][i + 1] + A[l]);
            }
            for (int i = 0; i <= n; i ++)
                Dp[0][i] = Dp[1][i];
        }
        return Dp[0][0];
    }
}
namespace Greedy
{
    vector<int> L, R;
    bool cmp(int u, int v)
    {
        return u > v;   
    }
    void Init()
    {
        L.clear();
        R.clear();
    }
    int Solve()
    {
        Init();
        for (int i = 1; i <= n; i ++)
        {
            if (s[i] == '(')
                L.push_back(A[i]);
            else R.push_back(A[i]);
        }
        sort(L.begin(), L.end(), cmp);
        sort(R.begin(), R.end(), cmp);
        int ret = 0;
        for (int i = 0; i < L.size() && i < R.size(); i ++)
        {
            int tuple = L[i] + R[i];
            if (tuple < 0) break ;
            ret += tuple;
        }
        return ret;
    }
}
int main()
{
    freopen("bracket.in", "r", stdin);
    freopen("bracket.out", "w", stdout);
    scanf("%d", &n);
    scanf("%s", s + 1);
    for (int i = 1; i <= n; i ++)
        scanf("%d", A + i);
    if (n <= 2000)
        ans = DP::Solve();
    else ans = Greedy::Solve();
    printf("%d\n", ans);
    return 0;
}

T2 连连看

emm...直接输出k可以得15分。$O(1)$

40-60分

枚举每一张牌，进行搜索，以转弯次数作为判断标准，看是否可以搜到。
时间复杂度：$O(nmk)$

100分

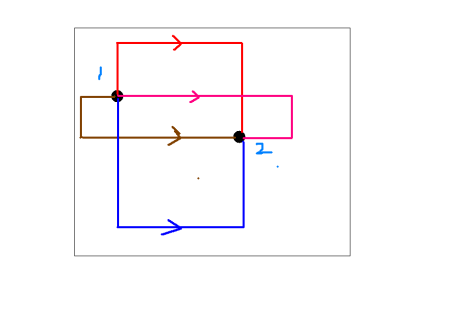
设1和2两个点为一对点，那么从1->2(2->1)无非只有以下4种情况，所以我们可以枚举每一个第一次转弯的点，判断是否可行。

代码

#include <cstdio>
#include <algorithm>
using namespace std;
#define N 1000 + 5
#define K 5000 + 5
int n, m, k, ans;
int Row[N][N], Column[N][N];
struct Point2D
{
    int x, y;
    Point2D() : Point2D(0, 0) {}
    Point2D(int x, int y) : x(x), y(y) {}
}Pos[K][2];
int main()
{
    freopen("linking.in", "r", stdin);
    freopen("linking.out", "w", stdout);
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 1; i <= k; i ++)
        for (int j = 0, x, y; j < 2; j ++)
        {
            scanf("%d%d", &x, &y);
            Pos[i][j] = Point2D(x, y);
            Row[x][y] = 1, Column[x][y] = 1;
        }
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++)
        {
            Row[i][j] += Row[i][j - 1];
            Column[i][j] += Column[i - 1][j];
        }
    for (int i = 1; i <= k; i ++)
    {
        bool ok = 0;
        for (int r = 1; !ok && r <= n; r ++)
        {
            int x_1 = Pos[i][0].x, x_2 = r, y = Pos[i][0].y;
            if (x_1 > x_2) swap(x_1, x_2);
            if (Column[x_2][y] - Column[x_1 - 1][y] > 1) continue ;
            int y_1 = Pos[i][0].y, y_2 = Pos[i][1].y;
            if (y_1 > y_2) swap(y_1, y_2);
            if (Row[r][y_2 - 1] - Row[r][y_1] > 0) continue ;
            x_1 = Pos[i][1].x, x_2 = r, y = Pos[i][1].y;
            if (x_1 > x_2) swap(x_1, x_2);
            if (Column[x_2][y] - Column[x_1 - 1][y] > 1) continue ;
            ok = true;
        }
        for (int c = 1; !ok && c <= m; c ++)
        {
            int y_1 = Pos[i][0].y, y_2 = c, x = Pos[i][0].x;
            if (y_1 > y_2) swap(y_1, y_2);
            if (Row[x][y_2] - Row[x][y_1 - 1] > 1) continue ;
            int x_1 = Pos[i][0].x, x_2 = Pos[i][1].x;
            if (x_1 > x_2) swap(x_1, x_2);
            if (Column[x_2 - 1][c] - Column[x_1][c] > 0) continue ;
            y_1 = Pos[i][1].y, y_2 = c, x = Pos[i][1].x;
            if (y_1 > y_2) swap(y_1, y_2);
            if (Row[x][y_2] - Row[x][y_1 - 1] > 1) continue ;
            ok = true;
        }
        ans += ok;
    }
    printf("%d\n", ans);
    return 0;
}

T3 数

30分

照题面模拟，需要手写两个函数。
判断$g(x)$与$x$大小函数：

bool bijiao(int x)
{
    int s[1000],ls=0,p;
    while(x)
    {
        s[++ls]=x%10;
        x/=10;
    }
    for(int i=1;i<=ls;i++)
    {
        if(s[i]!=0)
        {
            p=i;
            break;
        }
    }
    int l=p,r=ls;
    while(l<r)
    {
        if(s[l]>s[r])return 1;
        if(s[l]<s[r])return 0;
        l++;r--;
    }                               //  1 表示g(x)大， 0表示原数大。 
    return 1;
}

将$x$转为$g(x)$函数

int g(int x)
{
    int s[1000],ls=0,p,k=0,sum=0;
    while(x)
    {
        s[++ls]=x%10;
        x/=10;
    }
    for(int i=1;i<=ls;i++)
    {
        if(s[i]!=0)
        {
            p=i;
            break;
        }
        else k++;
    }
    for(int i=p;i<=ls;i++)sum=sum*10+s[i];
    for(int i=1;i<=k;i++)sum*=10;
    return sum;
}

75分

树上倍增，每一个数字都有一个值预期相对，那么可以在$x$与$f(x)$之间建一条边，最终形成一棵树，那么要求值得话，就可以树上倍增求值。

100分

需要离线做，预处理出$1e^7$的数的所对应得值，建出一棵查询树，每次询问就好了。

代码

#include <cstdio>
#include <algorithm>
using namespace std;
#define N 10000000 + 5
#define Q 200000 + 5
int n, htot, qtot, sz, Pow10[N], End10[N], G[N], Head[N], qHead[N], Stack[N], Ans[Q];
struct Edge
{
    int next, node;
}h[N];
struct Query
{
    int next, k, id;
}q[Q];
void addedge(int u, int v)
{
    h[++ htot].next = Head[u], Head[u] = htot;
    h[htot].node = v;
}
void addquery(int x, int k, int id)
{
    q[++ qtot].next = qHead[x], qHead[x] = qtot;
    q[qtot].k = k, q[qtot].id = id;
}
void Prepare()
{
    Pow10[0] = 1, End10[0] = 1;
    for (int i = 1; i < N; i ++)
    {
        int i_div_10 = i / 10;
        int i_mod_10 = i - i_div_10 * 10;
        Pow10[i] = Pow10[i_div_10] * 10;
        G[i] = G[i_div_10] + i_mod_10 * Pow10[i_div_10];
        if (i_mod_10 == 0)
            End10[i] = End10[i_div_10] * 10;
        else End10[i] = 1;
    }
    for (int i = 1; i < N; i ++)
    {
        G[i] = G[i] * End10[i];
        int f_i = (i <= G[i] ? i - 1 : G[i]);
        addedge(f_i, i);
    }
}
void dfs(int z)
{
    Stack[++ sz] = z;
    for (int i = qHead[z]; i; i = q[i].next)
    {
        int k = q[i].k, id = q[i].id;
        Ans[id] = (k >= sz ? 0 : Stack[sz - k]);
    }
    for (int i = Head[z]; i; i = h[i].next)
    {
        int d = h[i].node;
        dfs(d);
    }
    Stack[sz --] = 0;
}
int main()
{
    freopen("num.in", "r", stdin);
    freopen("num.out", "w", stdout);
    Prepare();
    scanf("%d", &n);
    for (int i = 1, x, k; i <= n; i ++)
    {
        scanf("%d%d", &x, &k);
        addquery(x, k, i);
    }
    dfs(0);
    for (int i = 1; i <= n; i ++)
        printf("%d\n", Ans[i]);
    return 0;
}