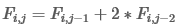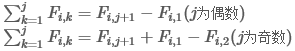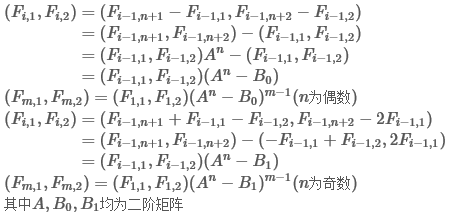@M1saki
2017-07-28T14:35:48.000000Z
字数 2058
阅读 1648
2017 Multi-University Training Contest - Team 2
acm 2017年7月 hdu 多校 组队训练
入口:2017 Multi-University Training Contest - Team 2
| rank | ac/all | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 174/882 | 8/11 | O | . | O | Ø | Ø | Ø | . | Ø | O | . | O |
| . | 尚未通过 | O | 当场通过 | Ø | 赛后通过 |
|---|
1001. Is Derek lying?
- 令为相同的个数,为不同的个数
- 那么要满足的条件为
1003. Maximum Sequence
预处理:a_i -= i ,易证明从最小的b开始选每次选最大的一定可以使结果最大。 证明思路:如果条件改为a_i<=max{a_j-j|b_k<=j<=n},那么b的顺序与最后的结果无关。条件改回来后,由于每次要计算一个数的最大值时都有a_(n+1)...a_(i-1)在范围中,所以每次只需让a_i - i尽可能大,那么就把大的数尽早用上,每次一定考虑尽量多的数字,这样取得的数字就尽可能的大。 所以说每次就是求区间最值,加在答案上。由于贪心的思路,每次要求的区间的下界是单调不降的,故可以用单调队列优化到O(n)的复杂度。 由于1 ≤ b_i ≤ n,对b排序可以用哈希排序(桶排序)完成。 进一步观察,可以发现这样贪心时 a_(n+1)...a_i 其实是单调不增的,所以并不需要每次求区间最值了,选第一个数时就选最大的,后面的选择顺序与最终结果无关了。
1004. Puzzle
性质1:数列的相邻互换将改变逆序对数的奇偶性。 证明1:易得。
性质2:去掉空格,剩余的木板从左到右从上到下看做数列,【操作】不改变数列逆序对的奇偶性。 证明2:左右移动:生成数列不改变,逆序对不变;上下移动:相当于移动的木板向前或向后进行m-1次相邻互换,但是空格最终要回到右下角,总的上下移动为偶数,所以总的相邻互换为偶数,由性质1可得证。
性质3:所有局面都可通过一定的操作得到如下局面: 以4*7为例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 X X 22 23 24 25 26 X 证明3:
a b X X X 可以证明任意初始局面,无论a、b初始在哪都可以通过一定操作使其位置如图所示。 证明脑补即可。
推广到任意局面:只需按顺序把数字当做a、b进行类似搬动,可保证性质3成立。
由以上性质,考虑完成性质3局面后右下角三个数字等价于局面。
枚举所有6种2*2局面发现:相同逆序对奇偶性的局面可以互相到达。 所以只需考虑原排列的逆序对数的奇偶性:偶的“YES”,奇的“NO”;
按题意生成原始排列,观察发现,每一轮数后方比该数小的数的数量(即对逆序对数的贡献)呈等差数列形式,公差,项数为,照此简化计算,不需要真正求出排列。
1005. Sdjpx Is Happy
- 先考虑不能交换的情况,能得到若干块。
- 交换必然发生在某块内。且必定是前缀和后缀的交换
- 预处理中间。
- 这里,预处理的信息可以有:
- 区间最值,
- 区间最多可分成几段的数目(作为上述的中间)
1006. Funny Function
对于任意i>=1,当j>=3时,有
通过归纳法可以得到
进而推导出
通过矩阵快速幂求解
1008. To my boyfriend
- 对于每种颜色单独考虑贡献
- 计算当前颜色的每个点将其作为最左边,其次最上的矩形个数。
- 假设枚举是从左到右枚举列,当前颜色向右可扩展的距离为
- 处理出当前这种颜色向左扩展时,行数的上下界,由于上下是独立的,那么此时的方案数为
1009. TrickGCD
令F(i)表示是i倍数的方案数,可以容易的通过预处理出前缀和后nlogn的时间内求出,之后利用预处理出莫比乌斯函数后进行简单的反演即可算出答案,加上快速幂,总复杂度nlogn^2
- 官方题解用的是莫比乌斯。
- 然而现场是用素数筛法+前缀和+容斥怼过去了。
- 枚举当前用了哪几个素数,假设这几个素数之积为,则可以将区间分成若干个大小都为的区间,每个区间内的数除以的值都相等。
1011. Regular polygon
容易得知只有正四边形可以使得所有的顶点为整数点。
(具体证明可参考杨景钦在2017的国家队论文)
所以正解即求出所有的正四边形个数。
枚举2个点,然后暴力判断另外2个点的位置是否存在。
复杂度 。